Topic Content:
- Conversion from Decimal to Octal
- Conversion of Octal to Decimal
- Worked Examples
An octal number is a number in base 8 and the place values increases in the power of 8.
Conversion from Decimal to Octal:
The conversion is similar to binary conversion but the only difference is that rather than dividing by 2 for the binary number, we would divide by 8 for an octal number until the last number is zero.
The following steps could be taken. Continue to divide the decimal number by 8 until the last division is zero and save the remainder as in the previous conversion.
Worked Example 1:
Convert 400 to octal
Solution
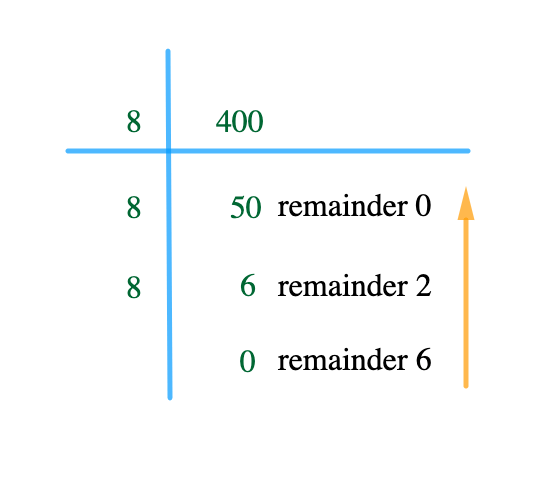
Answer: 40010 = 6208
Worked Example 2:
Convert 12 decimal to octal
Solution
You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!
Click on the button "Subscribe Now" below for Full Access!
Subscribe Now
Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!



Responses