Topic Content:
- Converting Numbers in Other Bases to Base Ten
- Worked Examples
A given number can be converted from any base to base 10 using the Expansion Method.
Once you are able to work out the place values, you can easily convert other base numbers to binary.
Let’s take a look at the following examples:
Worked Example 3.3.1:
Write the following numbers in expanded form.
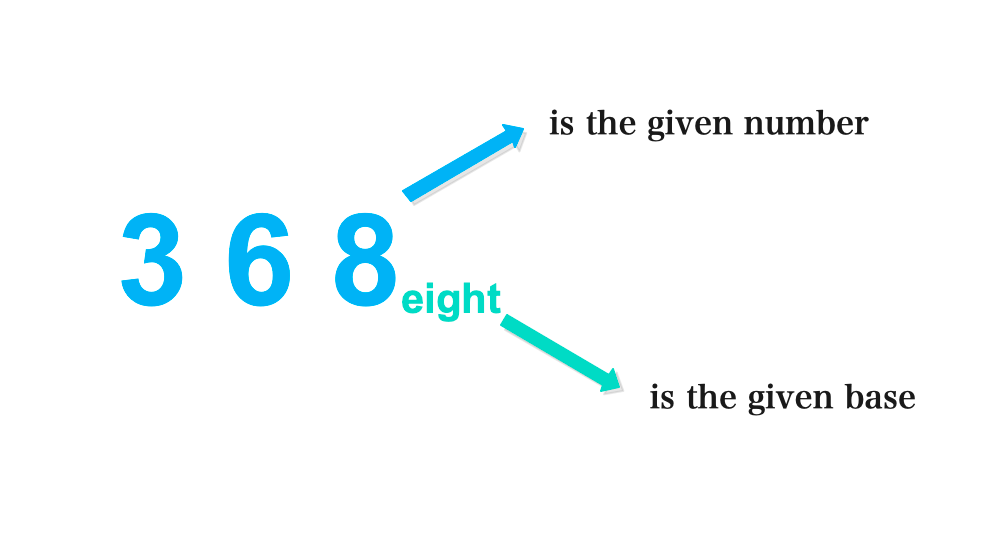
1. 356eight
2. 10321four
Solution
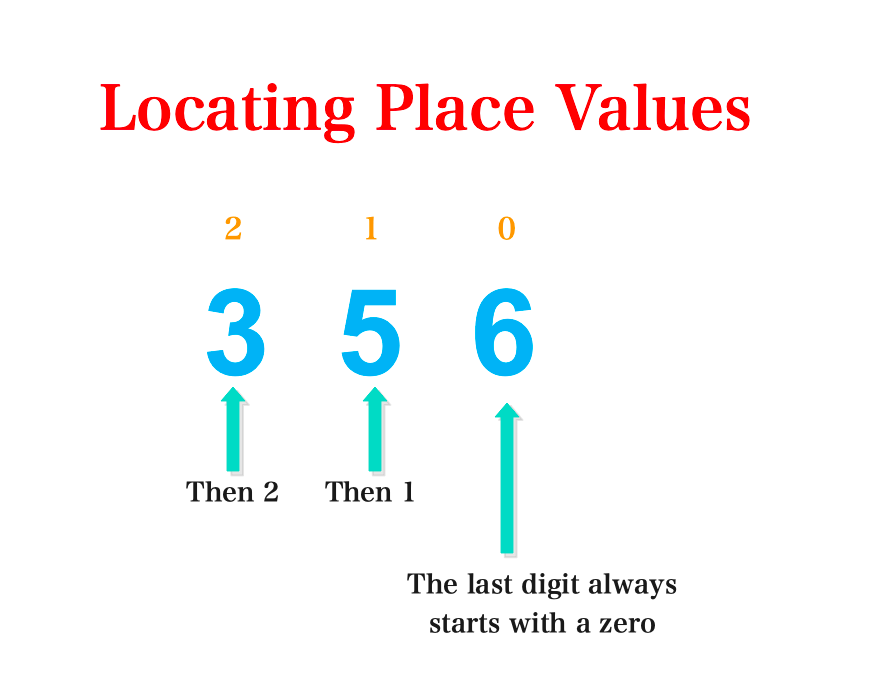
1st Step: To use the expansion method for conversion we first find the place numbers.
1. 356eight
Students often find it difficult to locate the place values. The easiest way is to start from the last digit to the first digit. The last Digit always starts with a 0, the digit that follows a 1, and so on. (0, 1 2, 3, etc)
2nd Step: Multiply each digit by its base number raised to the power of its place value
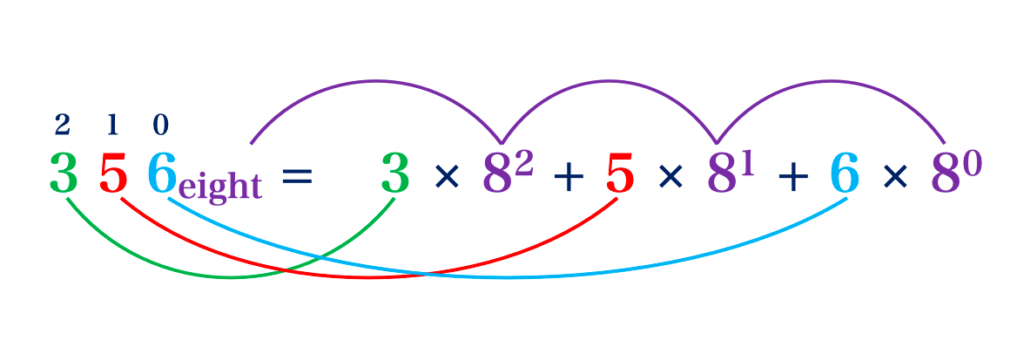
You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!
Click on the button "Subscribe Now" below for Full Access!
Subscribe Now
Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!



Responses