-
Whole Numbers I | Week 13 Topics1 Quiz
-
Whole Numbers II | Week 21 Topic1 Quiz
-
Counting in Base Two | Week 34 Topics1 Quiz
-
Arithmetic Operations | Week 43 Topics1 Quiz
-
Lowest Common Multiple (LCM) | Week 52 Topics1 Quiz
-
Highest Common Factor | Week 61 Topic1 Quiz
-
Fraction | Week 77 Topics1 Quiz
-
Basic Operations with Fractions I | Week 83 Topics1 Quiz
-
Basic Operations with Fractions II | Week 91 Topic1 Quiz
-
Directed Numbers | Week 103 Topics1 Quiz
-
Estimation and Approximation I | Week 113 Topics1 Quiz
-
Estimation and Approximation II | Week 126 Topics1 Quiz
Topic Content:
- Meaning of Place Value
- Rules for Finding Place Value
- Worked Examples
What is Place Value?
Place value is the value of a digit in a number based on its place or position.
Each digit, whole number or decimal number has a place value based on its position.
The value of a digit in the number is the digit multiplied by the place value.
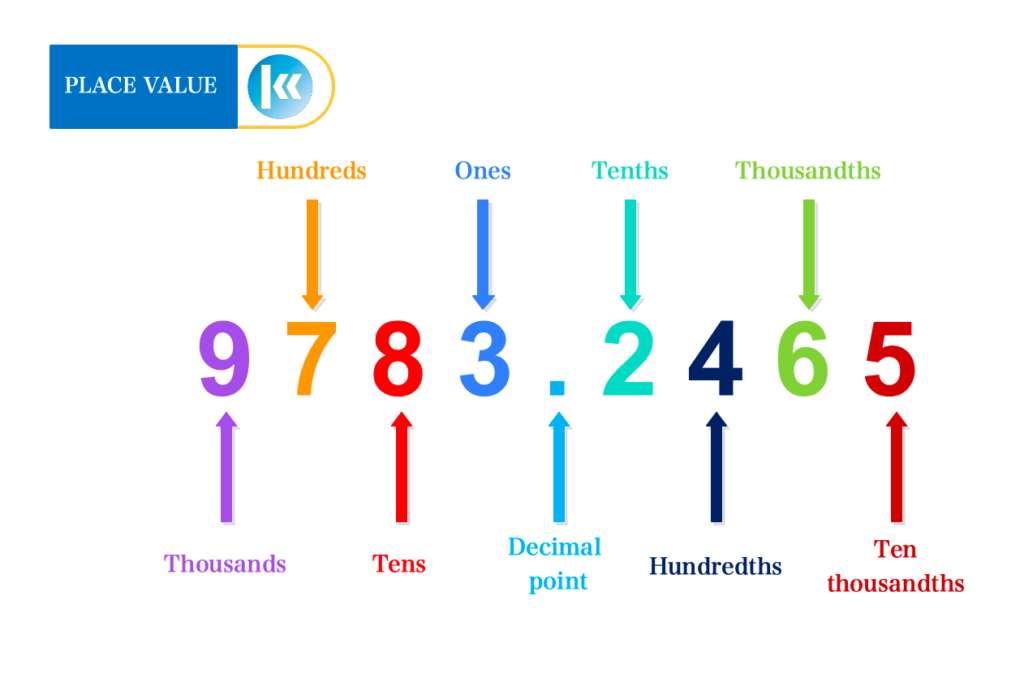
Example: 9783 . 2465
| Sum | ||
| 9 is in thousands | 9 × 1000 | 9000 |
| 7 is in hundreds | 7 × 100 | 700 |
| 8 is in tens | 8 × 10 | 80 |
| 3 is in units/ones | 3 × 1 | 3 |
| 2 is in tenths | 2 × \( \frac{1}{10}\) | 0.2 |
| 4 is in hundredths | 4 × \( \frac{1}{100}\) | 0.04 |
| 6 is in thousandths | 6 × \( \frac{1}{1000}\) | 0.006 |
| 5 is in ten thousandths | 5 × \( \frac{1}{10000}\) | 0.0005 |
| 9783.2465 |
Rules for Finding Place Value:
Below are the place value rules for the number 9783.2465 above;
Whole Numbers:
For whole numbers, always start from the decimal point and move to the left.
The first digit to the left of the decimal point is in the units/ones place, i.e. 3 units.
The second digit to the left of the decimal point is in the tens place, i.e. 8 tens.
The third digit to the left of the decimal point is in the hundreds place, i.e. 7 hundreds.
The fourth digit to the left of the decimal point is in the thousands place, i.e. 9 thousands.
Decimal Numbers:
For decimal numbers, always start from the decimal point and move to the right. It should be noted that there is no place value like “uniths”. Decimal place values start from tenths place.
The first digit to the right of the decimal point is in the tenths place, i.e. 2 tenths.
The second digit to the right of the decimal point is in the hundredths place, i.e. 4 hundredths.
The third digit to the right of the decimal point is in the thousandths place, i.e. 6 thousandths.
The fourth digit to the right of the decimal point is in the ten-thousandths place, i.e. 5 ten-thousandths.
Now let’s try some more examples.
Worked Example 1.1.1:
Give the digits in ones place and tenths place in the number 75.39
Solution:
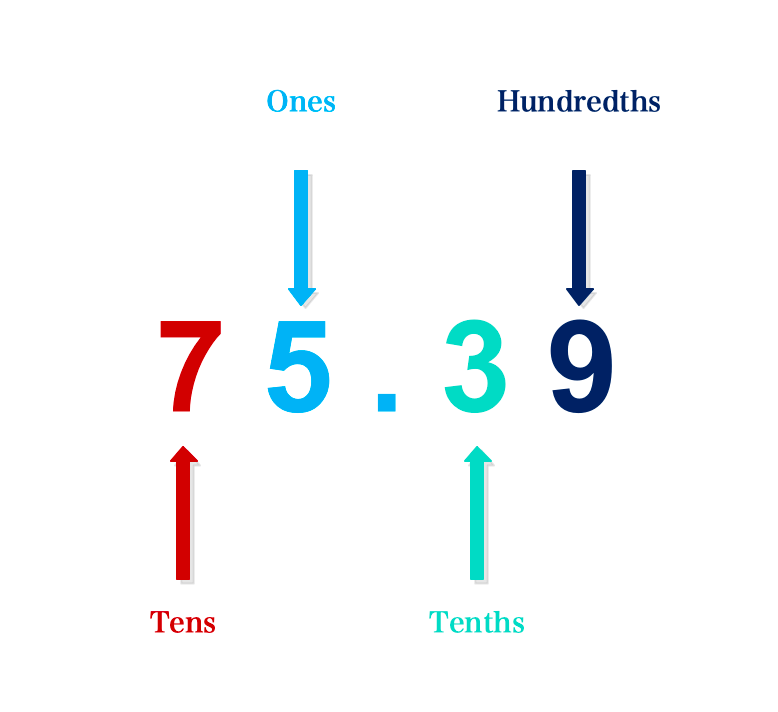
Step 1:
75.39
In the given number 75.39, the digit in ones place is 5 as it is the first digit to the left of the decimal point.
Step 2:
75.39
The digit in tenths place is 3 as it is the first digit to the right of the decimal point.
Worked Example 1.1.2:
Write down the place values for all the numbers in 9 453 276 . 1847
Solution:
9 – Millions
4 – Hundred thousands
5 – Ten thousands
3 – Thousands
2 – Hundreds
7 – Tens
6 – Units
. = Decimal point
1 – Tenths
8 – Hundredths
4 – Thousandths
7 – Ten thousandths
Worked Example 1.1.3:
What is the value of 5 in number 31.8752
Solution:
3 = Tens
1 = Units
. = Decimal point
8 = Tenths
7 = Hundredths
5 = Thousandths
2 = Ten thousandths
: The value of 5 is thousandths in number 31.8752
Worked Example 1.1.4:
What is the place value of 9 and 3 in 97814.060253?
Solution:
a. 9 in 97814.060253 is ten thousands
b. 3 in 97814.060253 is millionths
JSCE 2019 Mathematics Past Question
