Topic Content:
- Types & Properties of Quadrilaterals
A quadrilateral is a four-sided plane shape with four angles and the sum of all the angles is 360°.
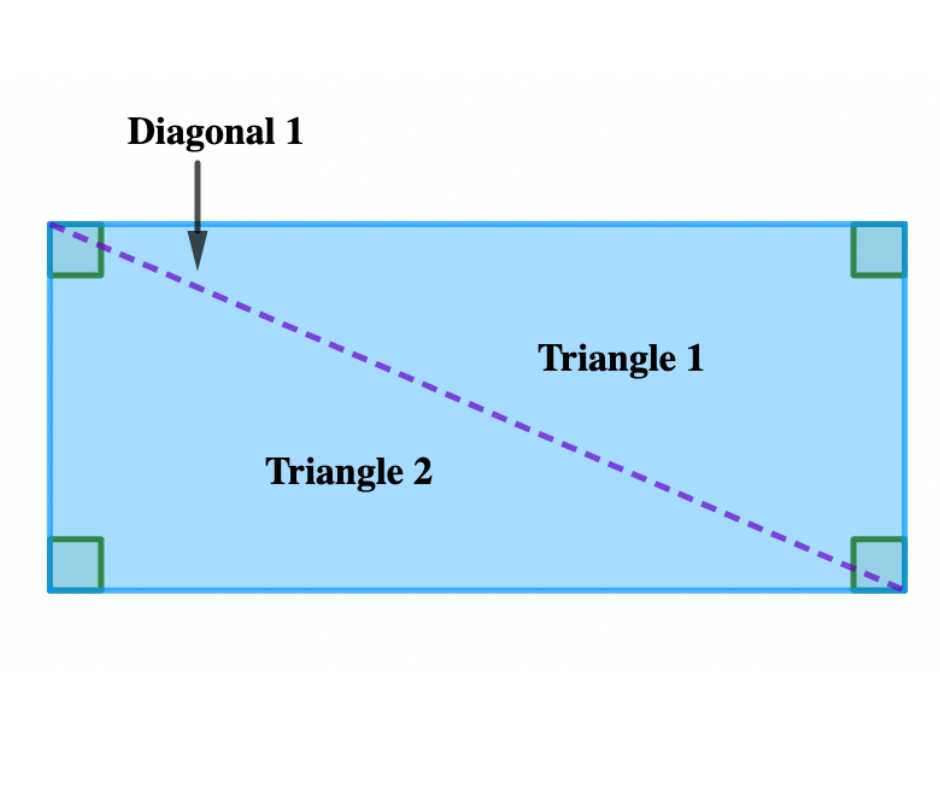
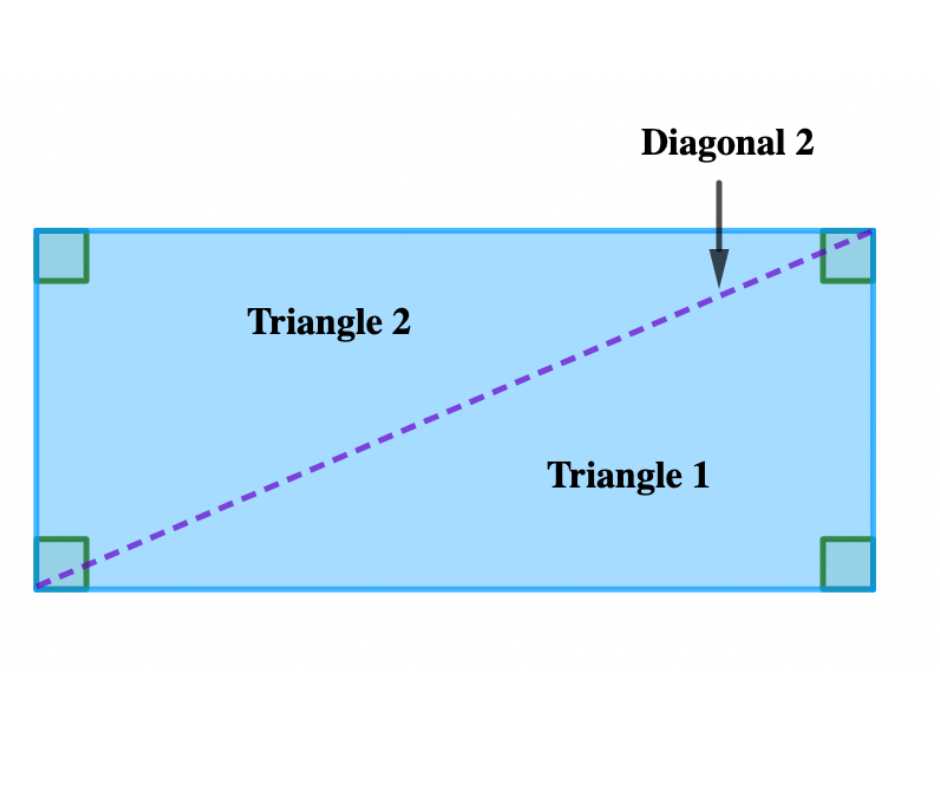
A diagonal is a straight line that connects the opposite corners of a quadrilateral. There are two diagonals and they divide a quadrilateral into two triangles. Each triangle has an angle sum of 180°. Therefore, the total angle sum of the quadrilateral is 360°.
Types of Quadrilaterals:
1. Parallelogram
2. Rhombus
3. Rectangle
4. Square
5. Trapezium
6. Kite
Parallelogram:
You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!
Click on the button "Subscribe Now" below for Full Access!
Subscribe Now
Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!



Responses