Area of a Square

 A square has all its sides equal

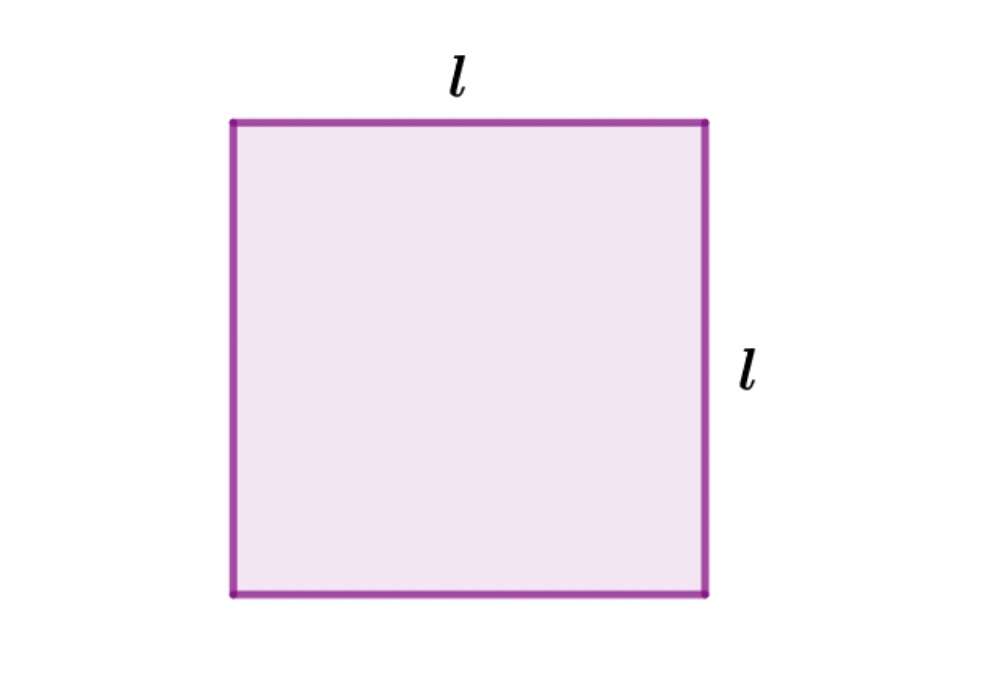
Let l  =  length of one side of a square.

Area  = \( \scriptsize l \: \times \: l = l^2 \)

Area  =  \( \scriptsize l^2 \)

A = \( \scriptsize l^2 \)

If Area  (A)  is given, then l can be found by taking the square root of both sides.

\( \scriptsize \sqrt{l^2} = \sqrt{A} \)

\( \scriptsize \therefore \: l = \sqrt{A} \)

Example 8.3.1: 

A square room is 500 cm long. Find the area in: 

(a) Square centimetres
(b) Square metres

Solution

(a) Area of the room = l²

= l  ×  l

= 500 cm   ×   500 cm

= 250 000 cm²

(b) In Square meters:

1 cm² = \( \frac{1}{10000} \scriptsize \: or \: 0.0001 \: m^2\)

250 000 cm² = \( \scriptsize 250,000 \: \times \: \normalsize \frac{1}{10000} \\ \scriptsize = 25\:m^2\)

Example 8.3.2:

The area of a square hall is 225 m². Find the length of one side of the square.

Solution

Area = l²

\( \scriptsize l = \sqrt{A} \)

\( \scriptsize l = \sqrt{225} \)

\( \scriptsize l = 15\:m \)

The length of the square is 15 m