Topic Content:
- Definition of a Circle
- Parts of a Circle
- Types of Circles
- Dividing a Circle into Four Equal Parts
- Dividing a Circle into Eight Equal Parts
- Dividing a Circle into Twelve Equal Parts
A circle can be defined as the locus of points, moving from a fixed point which is the centre of the circle to a fixed distance, which is the circumference.
The circumference is always equidistant from the centre.
Parts of a Circle:
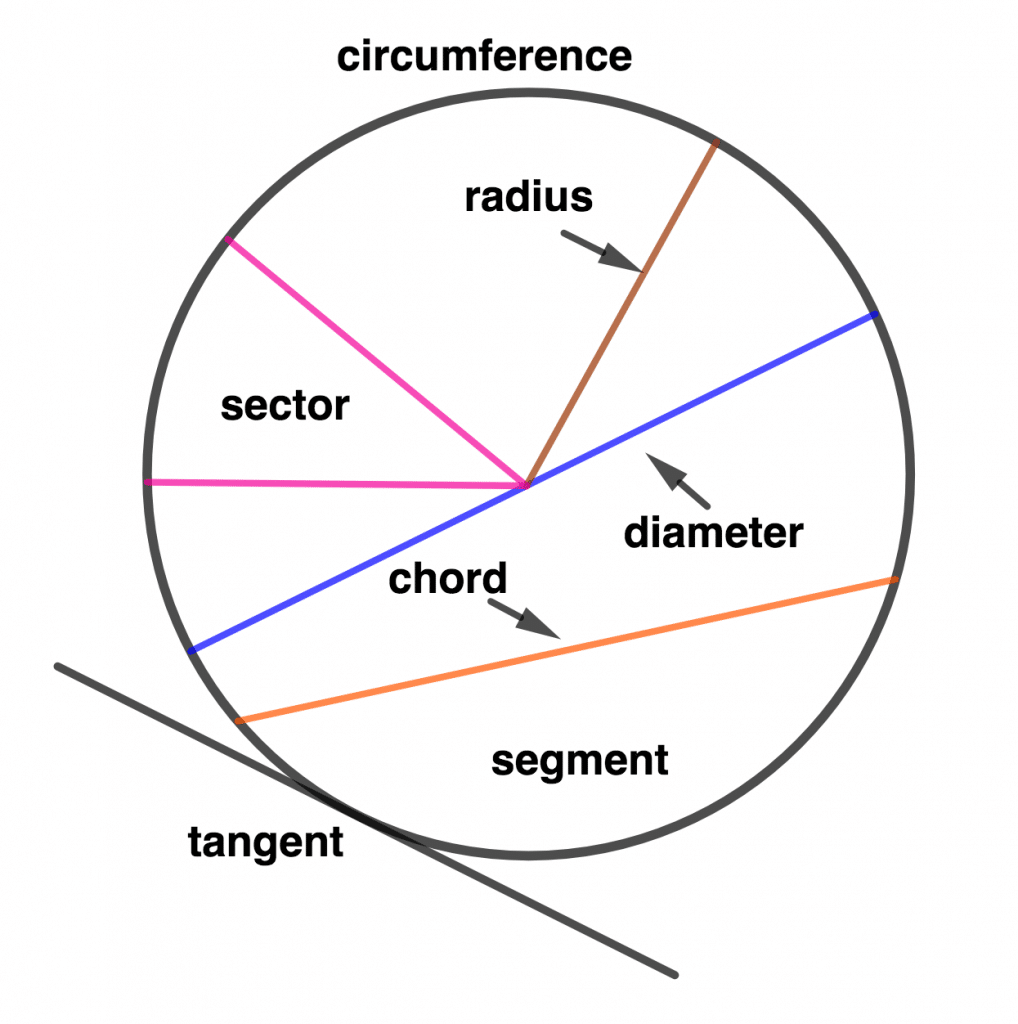
Parts of the circle include:
i. Circumference: This is a curved line around a circle or the outer part of a circle.
ii. Diameter: It is a straight line that passes through the centre of a circle and touches the circumference at both sides.
iii. Radius: It is a straight line drawn from the centre of a circle to touch the circumference.
Radius = \( \frac{diameter}{2} \)
Diameter = Radius × 2
You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!
Click on the button "Subscribe Now" below for Full Access!
Subscribe Now
Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!



Responses