Lesson Progress
0% Complete
Topic Content:
- Construction of Square
- Given the Length of Sides
- Given the Length of Its Diagonal
Construction of Square Given the Length of Sides:
Steps:
- Draw a line segment AB of a given length.

- Extend line AB to the right.

- Set the compasses on B and any convenient width. Draw an arc on each side of B, creating the two points E and F.
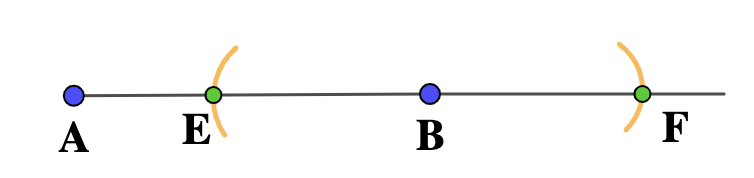
- With the compasses on F and any convenient width, draw an arc above point B.
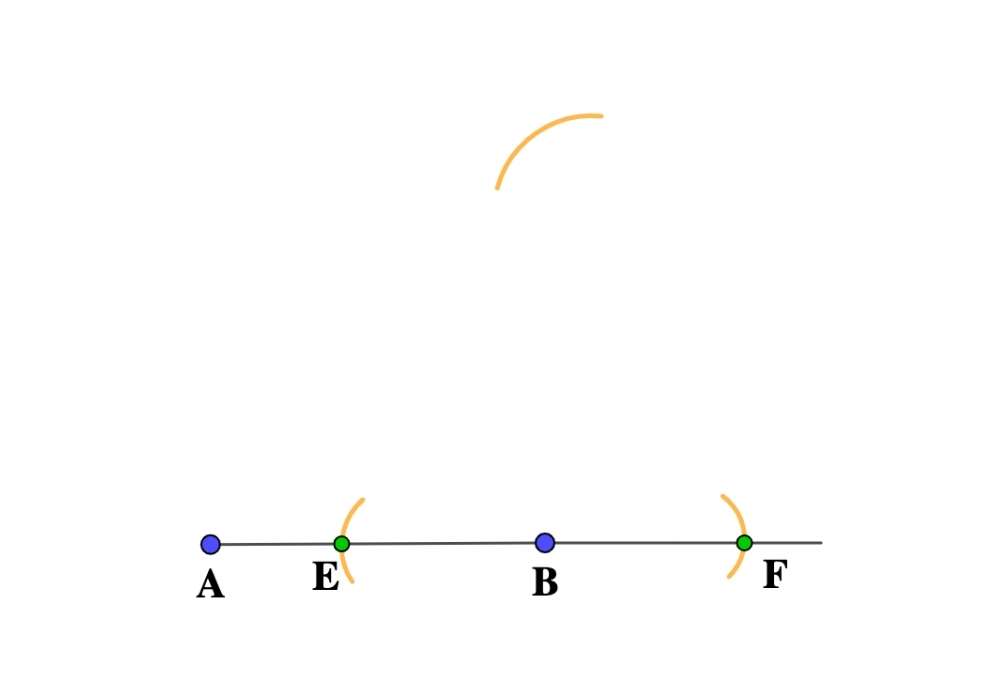
- Without changing the compasses’ width, place the compasses on E and draw an arc above B, crossing the previous arc, and creating point G
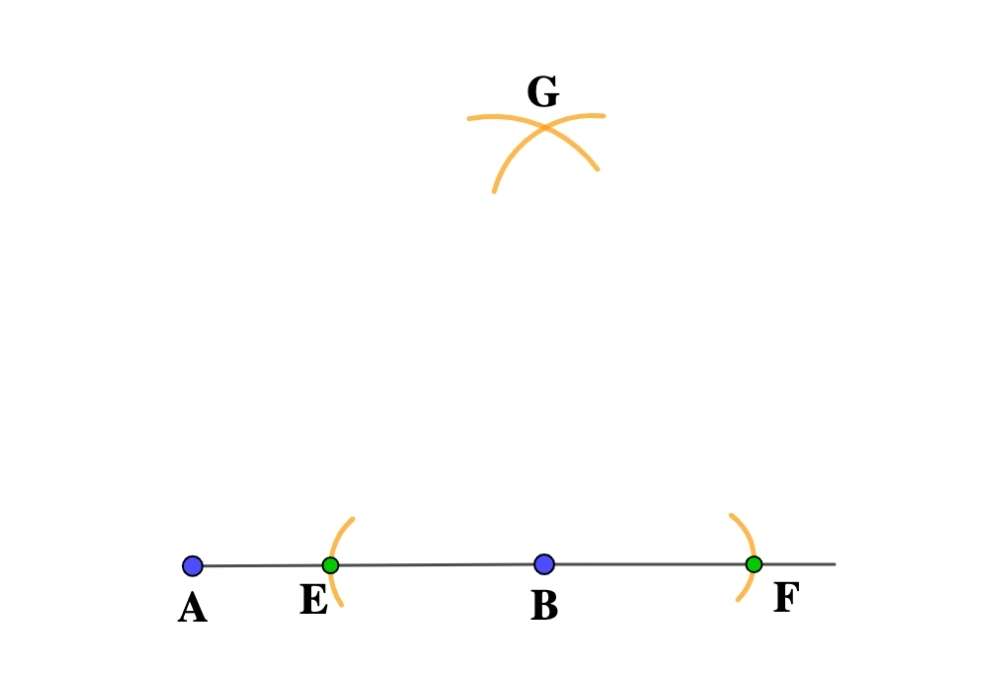
- Draw a Line from B through G
You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!
Click on the button "Subscribe Now" below for Full Access!
Subscribe Now
Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!



Responses