Factors, Multiples & Prime factors

Factors: 

The factors of a number are the whole numbers that divide the number without any remainder. e.g. the factors of 18 may be found as follows:

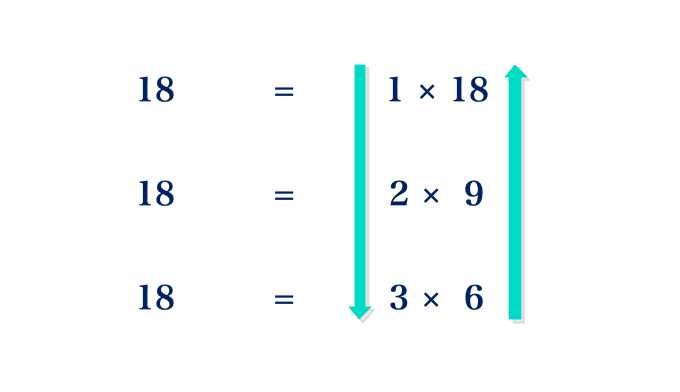
Factors of 18  are  1, 2, 3, 6, 9, 18

Multiples:

A multiple of a whole number is obtained by multiplying it by any whole number e.g.

The multiples of 4 are

4 × 1, 4 × 2, 4 × 3, 4 × 4, 4 × 5, 4 × 6 …..

which are  4, 8, 12, 16, 20, 24, …. etc

Worked Example 1.2.1:

a. Find all the factors of 36
b. State which of these factors are even
c. State which of these factors are odd

Solution

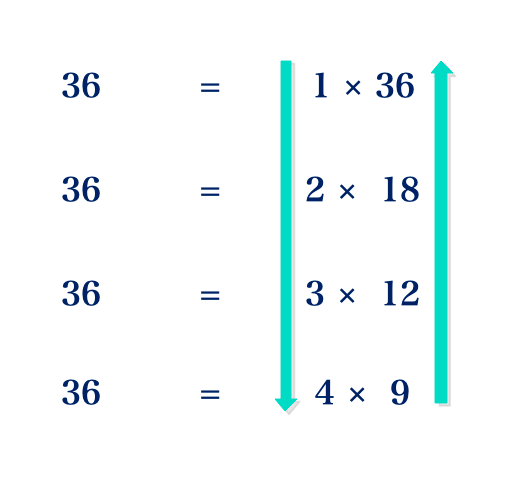
a. Factors  of 36  =  1, 2, 3, 4, 9, 12, 18 and 36

b. Even numbers are  2, 4, 12, 18 and 36

c. Odd numbers are  1, 3 and 9

Worked Example 1.2.2:

a. Write the first five multiples of 12
b. Which of them are multiples of 8

Solution:

a. Multiples of 12 are

12 × 1 = 12
12 × 2 = 24
12 × 3 = 36
12 × 4 = 48
12 × 5 = 60

Multiples of 12 are  12, 24, 36, 48 and 60

b. The multiples of 8 in 12, 24, 36, 48 and 60 

are 24 and 48

because; 

24  =  3 × 8 
48  =  8 × 6

Prime Number:

A prime number is a number that can only be divided by 1 and itself. It has only two factors.

Examples are;

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 83, 89, 91, 97 etc.

Prime factor:

A prime factor is a factor that is also a prime number e.g.

The factors of 20 are 1, 2, 4, 5, 10, and 20.

Out of these the prime factors of 18 are 2 and 5.

Product of Prime factors:

A given number can be expressed as a product of its prime factors. This is achieved by successive or repeated division by prime factors.

Worked Example 1.2.3:

Express the following numbers as a product of their prime factors. Express your answer in index form.  

(a)  36   
(b)  320   
(c)  336   

Solution

(a) 36 

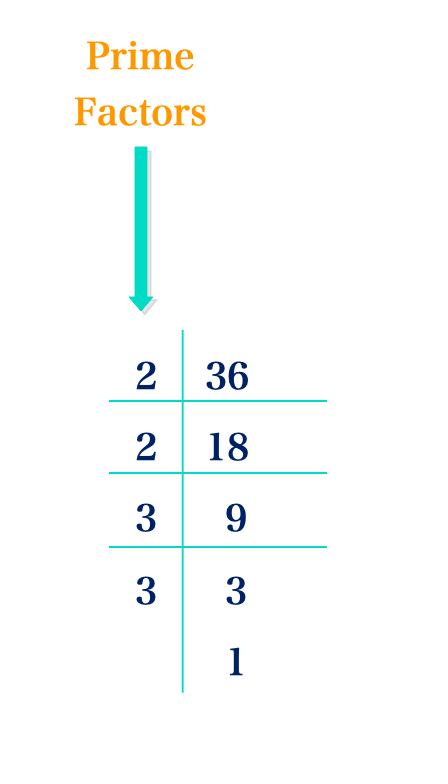
36 = 2 × 2 × 3 × 3 = 2² × 3²

(b) 320 

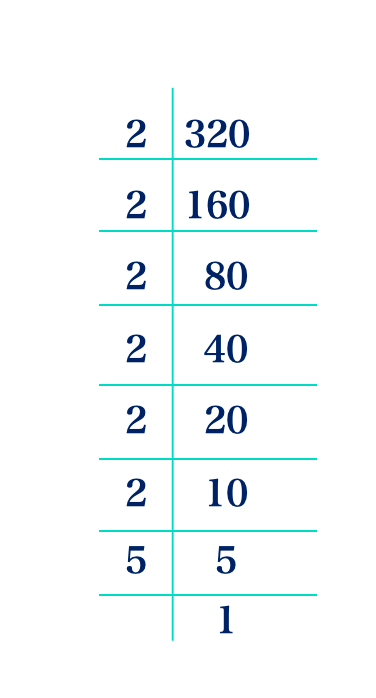
320  = 2 × 2 × 2 × 2 × 2 × 2 × 5  =  2⁶ × 5

(c) 336

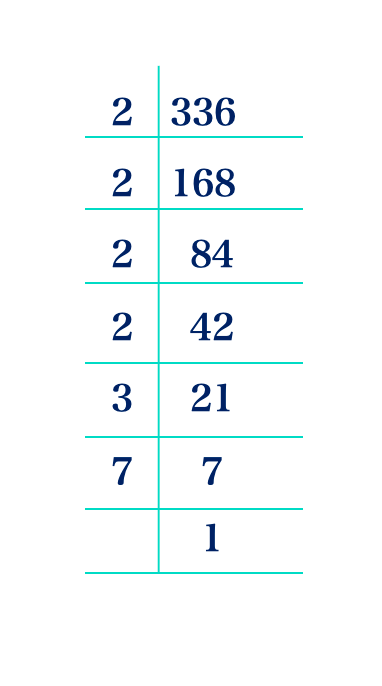
336 = 2 × 2 × 2 × 2 × 3 × 7  =  2⁴ × 3 × 7