-
Transactions in the Homes and Offices8 Topics1 Quiz
-
Expansion and Factorization of Algebraic Expressions4 Topics1 Quiz
-
Algebraic Expansion and Factorization of Algebraic Expression4 Topics1 Quiz
-
Algebraic Fractions I4 Topics1 Quiz
-
Addition and Subtraction of Algebraic Fractions2 Topics1 Quiz
-
Solving Simple Equations4 Topics1 Quiz
-
Linear Inequalities I4 Topics1 Quiz
-
Linear Inequalities II2 Topics1 Quiz
-
Quadrilaterals2 Topics1 Quiz
-
Angles in a Polygon4 Topics1 Quiz
-
The Cartesian Plane Co-ordinate System I3 Topics1 Quiz
-
The Cartesian Plane Co-ordinate System II1 Topic1 Quiz
Lesson Progress
0% Complete
Topic Content:
- Angles between Lines and Triangles – Worked Examples
Example 10.2.1:
Find the value of the lettered angles.
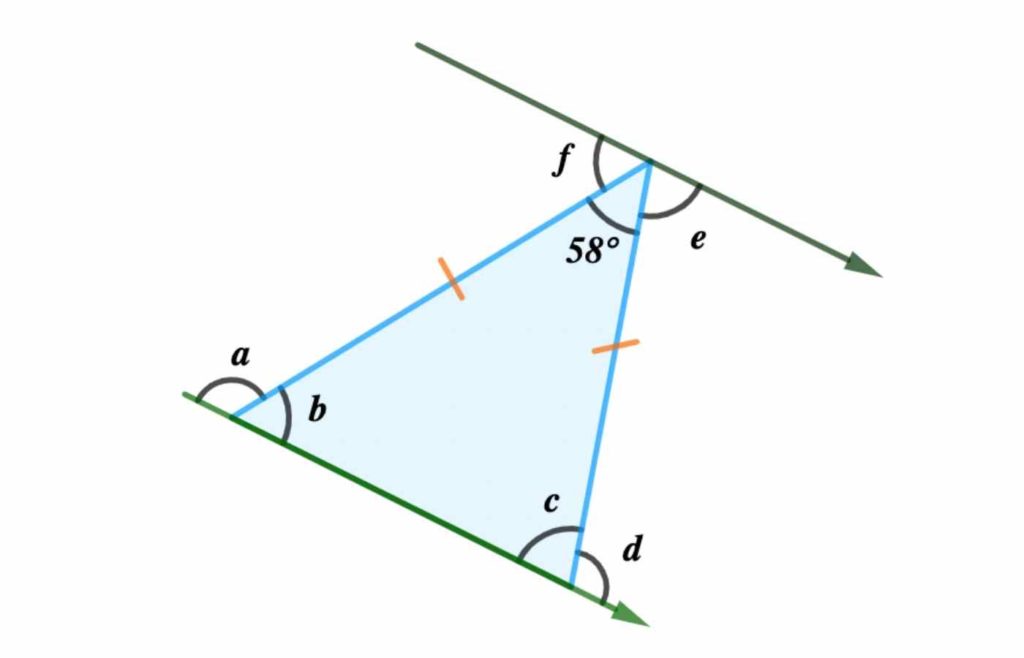
Solution:
Check if you have parallel lines. There are parallel lines so let’s apply angles in parallel lines.
But, let’s solve the angles
🔒 KOFA STUDY
Unlock This Topic
This topic is available to course subscribers.
Subscribe to continue this course.
- 📚 Continue this topic
- 📝 Attempt quizzes
- 📈 Track your learning progress
- 🪙 Earn KofaCoins
🚀 Unlock every topic, quiz and Kofa Arcade challenge in this course.
Already subscribed? Log in
Maths
Great one…preferred u added more.