Number Bases

The usual system of counting in recent times is called the decimal or denary system.

This system enables us to write small or large numbers using a combination of digits.

Example:  6843,   614.35

Each digit in a number has a place value.

For example, 8321 means 8 thousands,  3 hundreds, 2 tens, 1 unit

This can be shown using powers of 10 as follows:

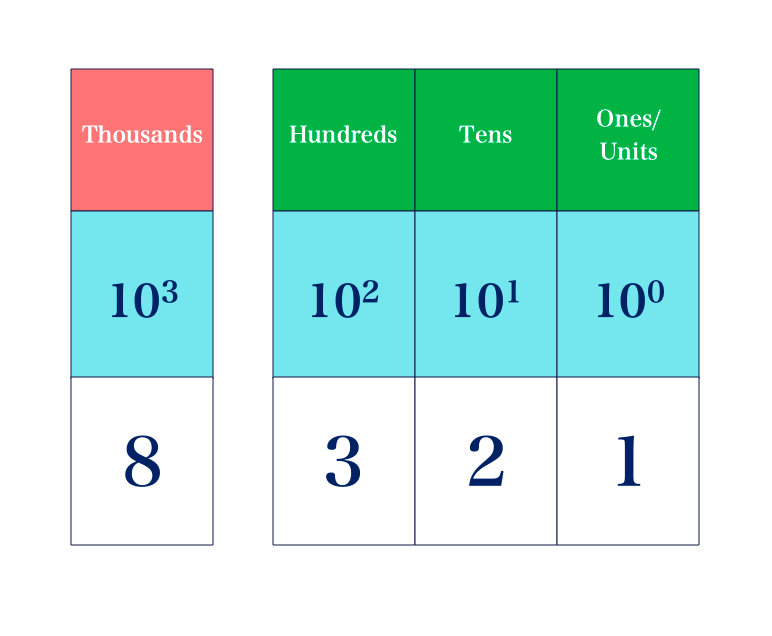
This can be written in expanded notation as 

⇒ 8 × 10³  + 3 × 10² + 2 × 10¹ + 1 × 10⁰

⇒ 8 × 1000 + 3 × 100 + 2 × 10 + 1 × 1 

⇒ 8000 + 300 + 20 + 1

Also, the decimal fraction 0.532 means 5 tenths,  3 hundredths, 2 thousandths 

i.e. 0.532 = 5 × 10^-1 + 3 × 10^-2 + 2 × 10^-3

Numbers in base 10 are usually written without the subscript ten or 10

431_ten is simply written as 431.

Apart from base 10, numbers are counted in other bases such as base two, base five, base seven, base eight etc.

Note: Numbers in other bases are also written in expanded notation.

For example, 

158 in base five is 

158 = 1 × 5² + 5 × 5¹ + 8 × 5⁰

= 1 × 25 + 5 × 5 + 8 × 1

Any number raised to the power 0 = 1 so in the above example 5⁰ = 1.

Worked Example 1.1.1:

Write the following numbers in expanded form.

a. 5314.23 
b. 31506_eight 
c. 232.01_five 
d. 5097_ten
e. 163.07_ten

Solution

a. 5314.23  means  5314.23 _ten

⇒ 5 × 10³ + 3 × 10² + 1 × 10¹ + 4 × 10⁰ + 2 × 10^-1 + 3 × 10^-2

b. 31506_eight  =  3 × 8⁴ + 1 × 8³ + 5 × 8² + 0 × 8¹ + 6 × 8⁰

c. 232.01_five  = 2 × 5² + 3 × 5¹ + 2 × 5⁰ + 0 × 5^-1 + 1 × 5^-2

d. 5097_ten = 5 × 10³ + 0 × 10² + 9 × 10¹ + 7 × 10⁰

e. 163.07_ten = 1 × 10² + 6 × 10¹ + 3 × 10⁰ + 0 × 10^-1 + 7 × 10^-2