Similar Triangles

Similar triangles are equiangular and the ratios of corresponding sides are equal. Equiangular means that the angles of one triangle are equal to the angles of the other. 

Two triangles are similar if the: 

1. Corresponding angles are equal
2. Ratios of the corresponding sides are equal. 

To show that two triangles are similar it is not necessary to satisfy all of the above conditions. However, one of the following conditions is sufficient to show that two triangles are similar. 

a) Two triangles are similar if two angles of one triangle are equal to two angles of the other. 

For example in ∆ABC and ∆XYZ, shown below if ∠A = ∠X, ∠B = ∠Y, then ∠C = ∠Z since the three angles in each triangle must add up to 180°.

 

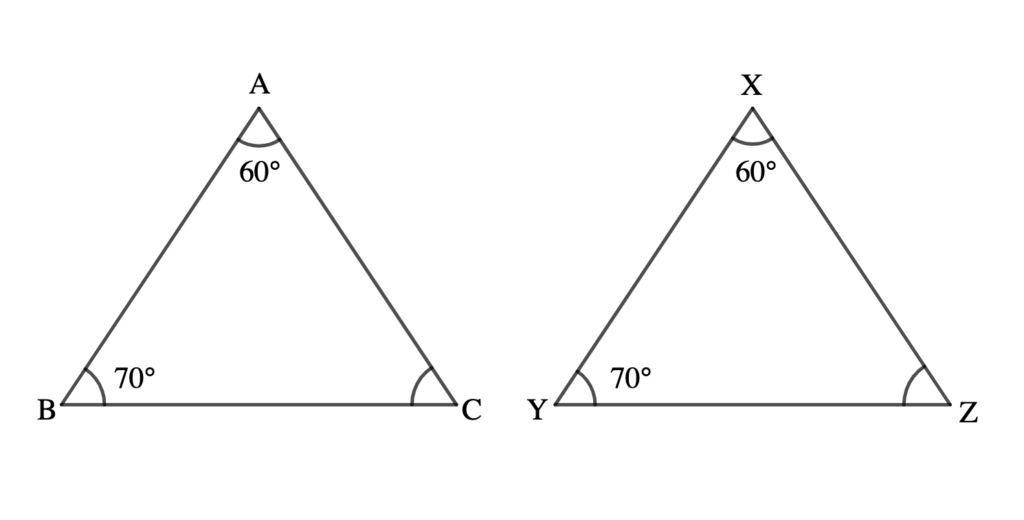
∠A = ∠X, ∠B = ∠Y;

∠C = ∠Z = 50°. Since the three angles in each triangle must add up to 180°. 

Thus ∆ABC and ∆XYZ are similar 

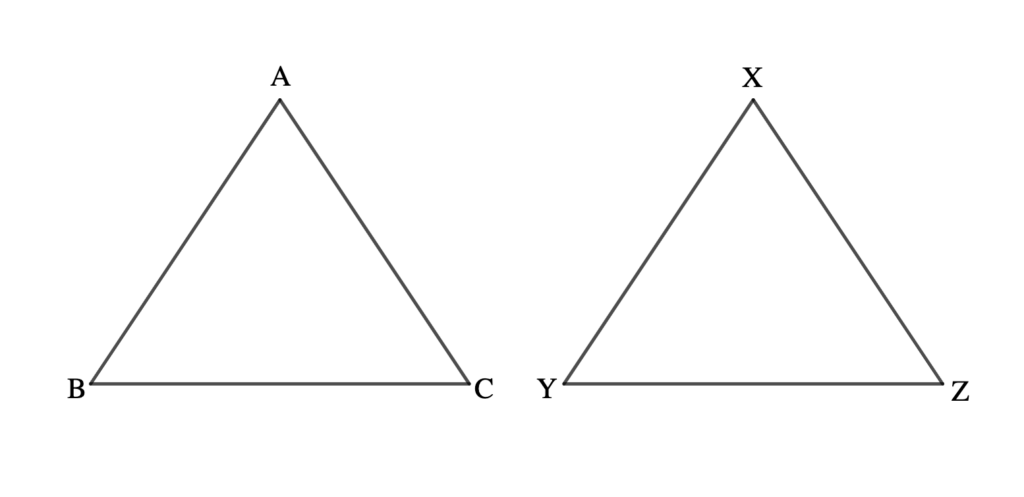
b) Two triangles are similar if two pairs of corresponding sides are proportional and the corresponding angles between them are equal.

Two pairs of sides are AB and XY; BC and YZ and the corresponding angles are ∠B and ∠Y, then 

\( \frac{AB}{XY} = \frac{BC}{YZ} \) and \( \scriptsize \angle \)B  =  \( \scriptsize \angle \)Y 

OR

\( \frac{XY}{AB} = \frac{YZ}{BC} \) and \( \scriptsize \angle \)B  =  \( \scriptsize \angle \)Y 

c)  Two triangles are similar if the ratios of their corresponding lengths (sides) are equal. 

\( \frac{AB}{XY} = \frac{AC}{XZ}= \frac{BC}{YZ} \)

OR

\( \frac{XY}{AB} = \frac{XZ}{AC}= \frac{YZ}{BC} \)

It is essential to name similar figures with their letters in corresponding order.

Example 4.3.1:

Show that triangles ABC and EFG are similar 

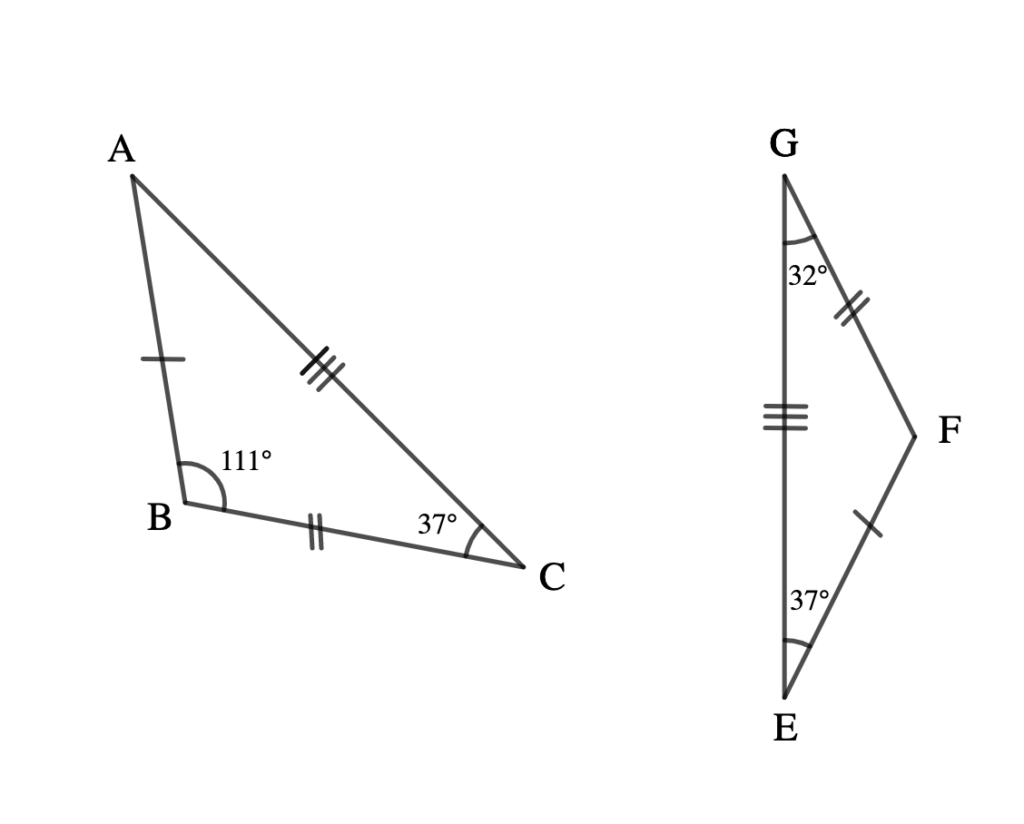
In ΔABC: