-
Introduction to Economics3 Topics1 Quiz
-
Basic Concept of Economics4 Topics1 Quiz
-
Basic Tools for Economic Analysis8 Topics1 Quiz
-
Measure of Central Tendency4 Topics1 Quiz
-
Theory of Demand & Supply I5 Topics1 Quiz
-
Theory of Demand & Supply II7 Topics1 Quiz
-
Theory of Production I7 Topics1 Quiz
-
Theory of Production II4 Topics1 Quiz
-
Basic Economic Problems of the Society1 Topic1 Quiz
-
Economic System4 Topics1 Quiz
Lesson Progress
0% Complete
Topic Content:
- Definition of Demand Curve
- Example of Demand Curve
- Calculating the Slope of a Demand Curve
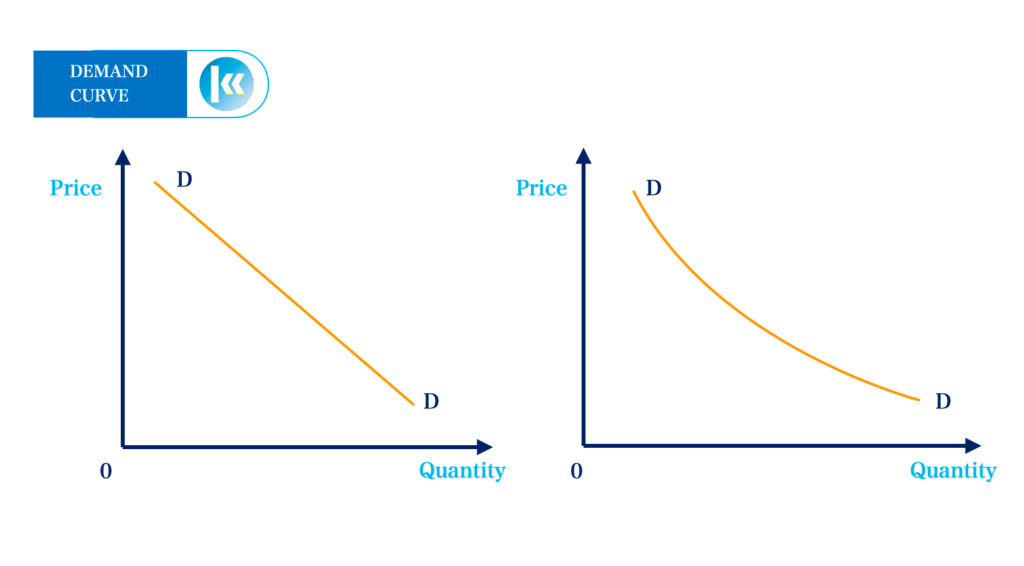
What is a Demand Curve?
A demand curve is a graphic representation of the relationship between price and quantity. It indicates the different quantities of a commodity demanded at different prices.
The demand curve slopes downward from left to right, showing that more will be bought at lower prices than at higher prices. This means that quantity demand rises as price falls.
It also means that an increase in price causes a fall in quantity demanded, that is, quantity demanded rises as price falls. A normal demand curve is negatively
🔒 KOFA STUDY
Unlock This Topic
This topic is available to course subscribers.
Subscribe to continue this course.
- 📚 Continue this topic
- 📝 Attempt quizzes
- 📈 Track your learning progress
- 🪙 Earn KofaCoins
🚀 Unlock every topic, quiz and Kofa Arcade challenge in this course.
Already subscribed? Log in
Like this content
Subscribe
Login
0 Comments
Oldest
