Topic Content:
- Meaning of Logarithm (Log) Table
- Features of a Log Table
- How to Use the Log Table
In mathematics, the logarithm table is used to find the value of the logarithmic function. The simplest way to find the value of the given logarithmic function is by using the log table.
Given below is the common log table (i.e., for base 10). This table can give the value of log x (which is also written as log10 x) for any x.

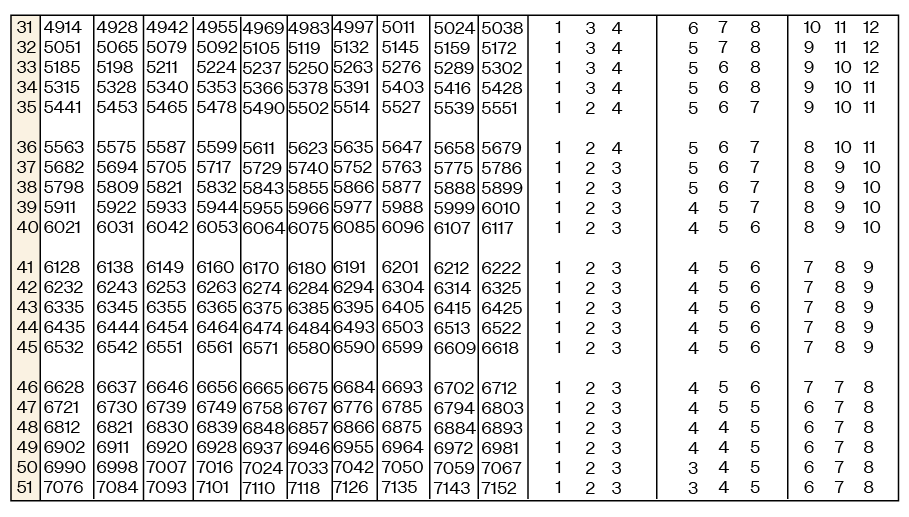
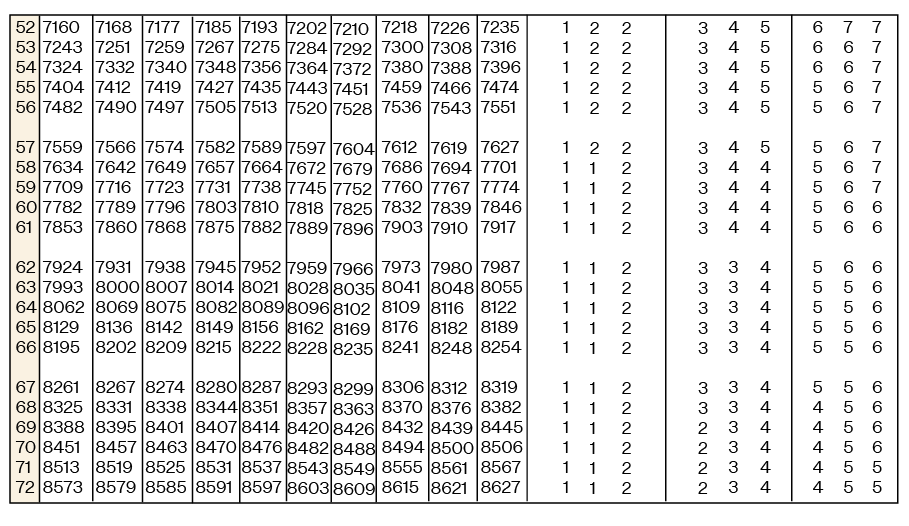
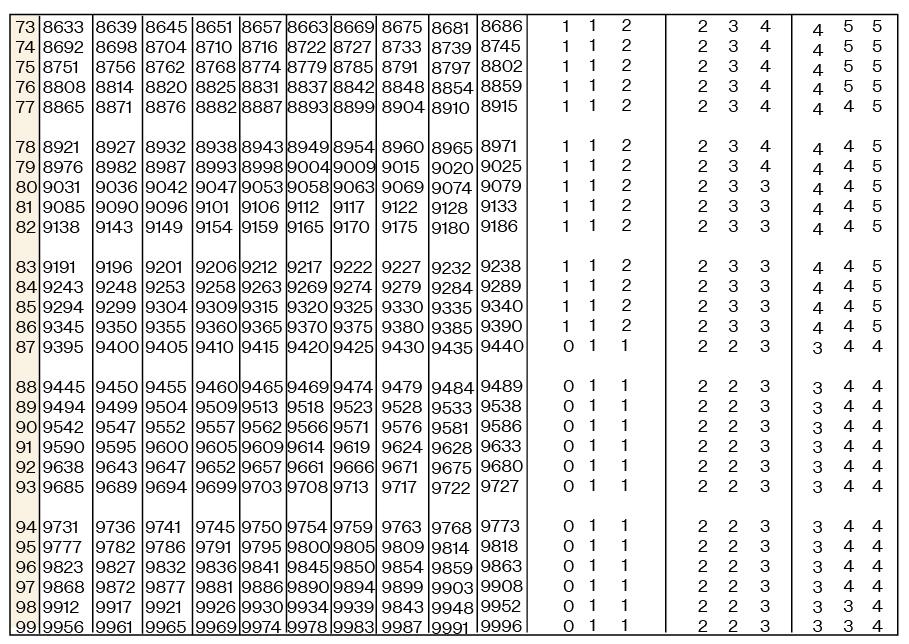
Features of a Log Table:
The log table mainly has 3 types of columns:
- The main column with numbers from 10 – 99 (all are 2 digit numbers)
- The differences column which shows the differences for the digits 0 – 9
- The mean differences column showing the mean differences from 1 – 9
There are also logarithm tables for base e (which is called the natural logarithm table) and for base 2 (which is called the binary logarithm table).
How to Use the Log Table?
The logarithm of any number consists of two parts: an integer(whole number) and a fraction after the decimal point.
The integral part is called the characteristic and the fractional or decimal part is called the mantissa.
You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!
Click on the button "Subscribe Now" below for Full Access!
Subscribe Now
Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!



Cool thanks for the lesson