Topic Content:
- Modular Congruence
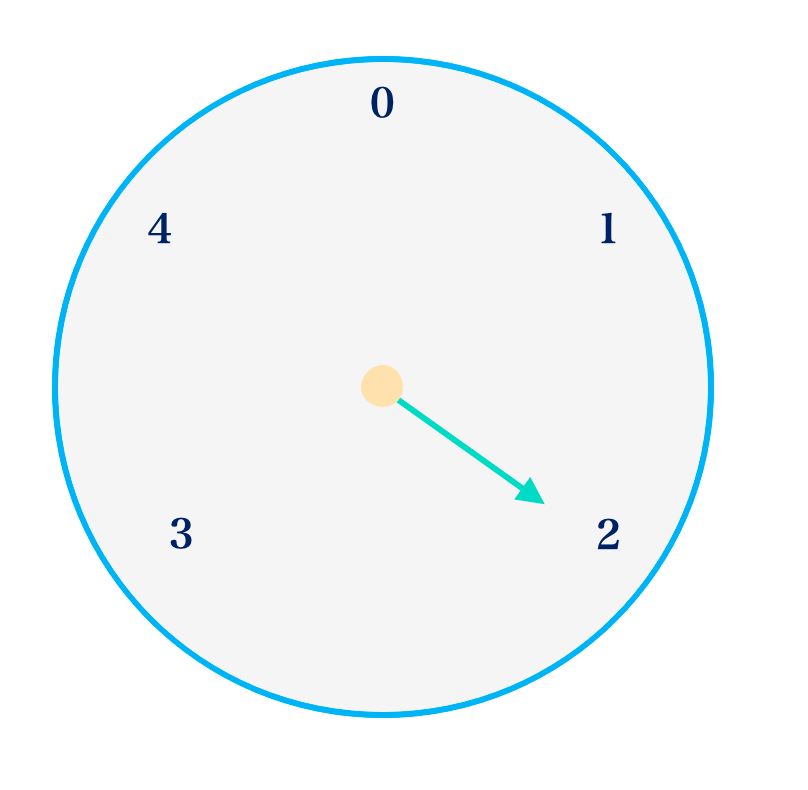
Consider the circle above numbered 0 to 4. These digits are the same as those used in the modulo 5 system.
Key-Point:
1. If the pointer is on 2 and is turned clockwise through 4 spaces, it will end up at 1.
- This is usually written as \( \scriptsize 2 + 4 \equiv 1 \:(mod\:5) \kern-1em \:\)
- Where the sign \( \scriptsize \equiv \) means “it’s congruent to”
⇒ \( \scriptsize 2 + 4 \equiv 1\: (mod\:5) \kern-1em\: \) means “2 plus 4 is congruent to 1 modulo 5”

2. If the pointer is on 2 and turns clockwise through 20 spaces, it will end up at 2.
- Thus, \( \scriptsize 2 + 20 \equiv 2 \:(mod\:5)\)
Example 4.2.1:
Simplify the following:
(i) 56 (mod 5)
(ii) 440 (mod 7)
Solution:
You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!
Click on the button "Subscribe Now" below for Full Access!
Subscribe Now
Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!



easy ready for the quiz
It’s really helpful