Topic Content:
- The Cyclic Event
- Definition of Modular Arithmetic
A good example of a cyclic event is the 12-hour clock. In the 12-hour clock arithmetic, the hour hand can move in both directions as shown in the diagram.
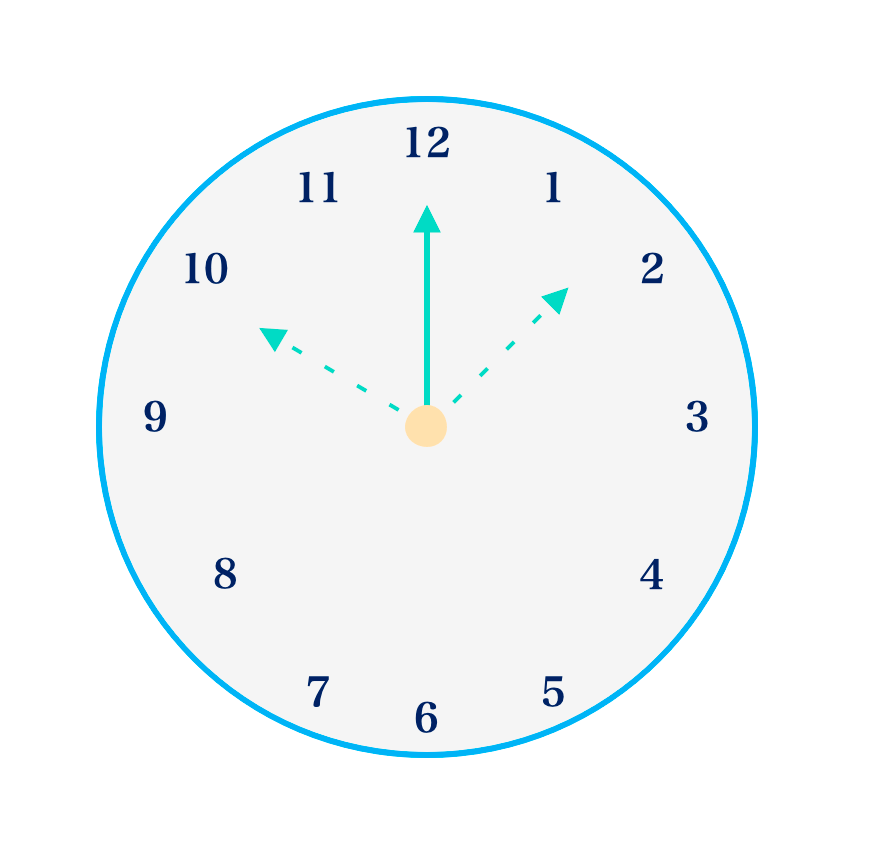
Example 4.1.1:
If the time is presently 9 o’clock, what would the time be in:
(i) 92 hours
(ii) 750 hours’ time?
Solution
(i) 92 hours = 92 ÷ 12 = 7 r 8
= ( 12 × 7) hrs + 8 hrs
= 9 o’clock + 8hrs
= 5 o’clock
This means the clock will start counting from 9 and turn clockwise 12 times. It will end up at 9 with an addition of 8 hours (+8 hrs).
You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!
Click on the button "Subscribe Now" below for Full Access!
Subscribe Now
Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!



Responses