Back to Course

SS1: MATHEMATICS - 1ST TERM

0% Complete
0/0 Steps
  1. Number Base System I | Week 1
    6 Topics
    |
    2 Quizzes
  2. Number Base System II | Week 2
    3 Topics
  3. Number Base System III | Week 3
    2 Topics
    |
    1 Quiz
  4. Modular Arithmetic I | Week 4
    2 Topics
  5. Modular Arithmetic II | Week 5
    3 Topics
  6. Modular Arithmetic III | Week 6
    4 Topics
    |
    1 Quiz
  7. Indices I | Week 7
    3 Topics
    |
    1 Quiz
  8. Indices II | Week 8
    1 Topic
    |
    1 Quiz
  9. Logarithms I | Week 9
    3 Topics
  10. Logarithms II | Week 10
    4 Topics
    |
    1 Quiz

Quizzes




  • Kofa Study
Lesson Progress
0% Complete

Topic Content:

  • Addition & Subtraction in Modular Arithmetic
Screenshot 2023 09 14 at 06.42.14

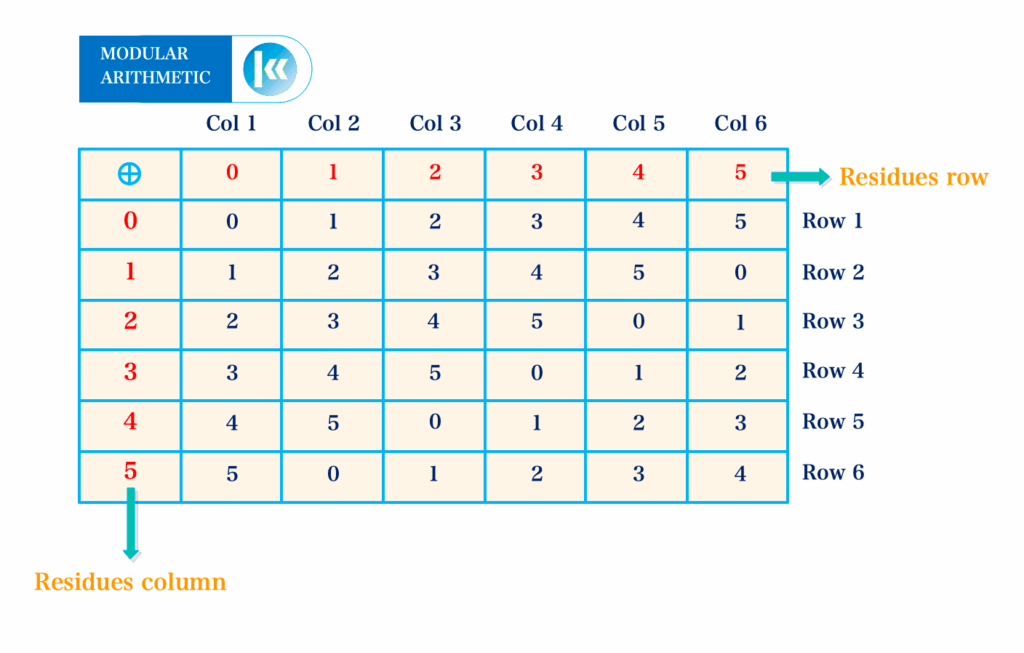
The diagram above shows addition in modulo 6 in which an element on the extreme left is added to an element on the top row, in that order. You will observe that the first column on the extreme left and the top row contain the same set of integers.

Example 5.2.1:

\( \scriptsize 3 \: \bigoplus \: 2 \)

Solution

Look for the number 3 on row 4 and the number 2 on column 3, they intersect at number 5.

Screenshot 2023 09 14 at 06.44.12

i.e.  \( \scriptsize 3 \: \bigoplus \: 2 = 5\:(mod\:6) \)

In the same vein, subtraction can be considered as the inverse operation of addition. So, in mod 6, we can use the addition table to work out subtraction:

Example 5.2.2:

\( \scriptsize 2 \: \circleddash \: 5 \)

Solution

 

You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!

Click on the button "Subscribe Now" below for Full Access!

Subscribe Now

Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!

avatar

Responses

Your email address will not be published. Required fields are marked *

Solution (i)

⇒ \( \scriptsize 54 \: \bigoplus \:  65 \: (mod\: 6) \)

Step 1

Add 54 and 65

i.e. 54 + 65 = 119 (mod 6)

Step 2

Take the answer of the addition to mod 6

= \( \frac{119}{6} \)

= 19 r 5

Step 3

119 = 19 × 6 + 5 (mod 6)

= 0 + 5 (mod 6)

∴ 119 (mod 6) = 5 (mod 6)

Solution (ii)

⇒ – 25 (mod 8)

=  (– 4 × 8) + 7 (mod 8)

= – 32 + 7 (mod 8)

= 0 + 7 (mod 8)

∴  – 25 (mod 8) = 7 mod 8

Solution (iii)

⇒ – 56 (mod 12)

= (– 5 × 12) + 4 (mod 12)

= – 60 + 4 (mod 12)

= 0 + 4 (mod 12)

∴   – 56 (mod 12) = 4 (mod 12)

Solution (iv)

⇒ 2 ⊖ 11 (mod 5)

2 – 11 (mod 5) = – 9 (mod 5)

=  – 5  × 2 + 1 (mod 5)

=  – 10 + 1 (mod 5)

= 0 + 1 (mod 5)

∴  2 – 11 (mod 5) = 1 (mod 5)

Solution (v)

⇒ 12 ⊖ 5 (mod 6)

12 – 5 (mod 6) = 7 mod 6

= 6 + 1 (mod 6)

= 0 + 1 (mod 6)

∴   12 – 5 (mod 6) = 1 (mod 6)

Solution (vi)

⇒ 5 ⊖ 20 (mod 11)

5 ⊖ 20 (mod 11) = – 15 (mod 11)

          =  –2 × 11 + 7 (mod 11)

          =  – 22 + 7 (mod 11)

           = 0 + 7 mod 11

∴     5 ⊖ 20 (mod 11) = 7 (mod 11)

Report

Harassment or bullying behavior
Contains mature or sensitive content
Contains misleading or false information
Contains abusive or derogatory content
Contains spam, fake content or potential malware

Block Member?

Please confirm you want to block this member.

You will no longer be able to:

  • See blocked member's posts
  • Mention this member in posts
  • Invite this member to groups
  • Message this member
  • Add this member as a connection

Please note: This action will also remove this member from your connections and send a report to the site admin. Please allow a few minutes for this process to complete.

Report

You have already reported this .
error: Alert: Content selection is disabled!!