Topic Content:
- Subtraction in Other Bases
Reminder of the rules of binary subtraction:
0 – 0 = 0
1 – 0 = 1
1 – 1 = 0
10 – 1 = 1
11 – 1 = 10
When you borrow a number during subtraction, it becomes the number of the base you are subtracting from.
For example, in Base 2 if you borrow a number the number you borrow becomes 2, Likewise in base 5 if you borrow a number it becomes 5.
Now, let’s take some examples.
Examples 1.5.1:
Evaluate the following:
1. 11000two – 111two
2. 20204six – 5125six
3. 72438 – 45368
4. 1A3516 – F7E16
1. 11000two – 111two
Solution
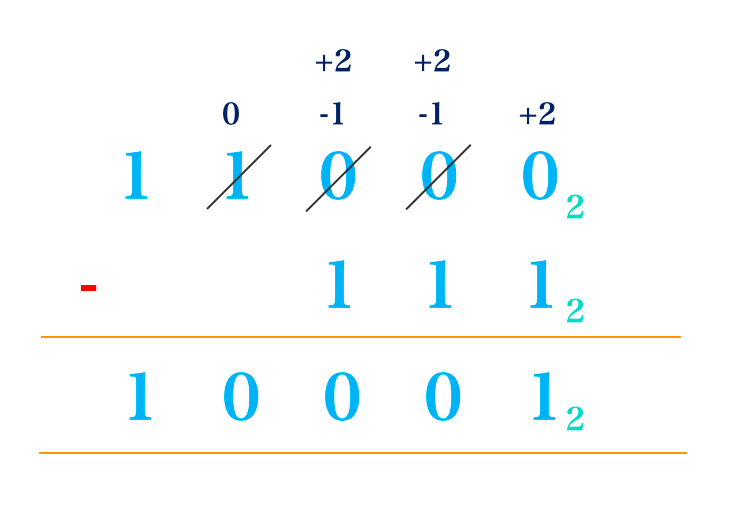
Explanation
1st Column (from right to left): 0 is smaller than 1 so we will have to borrow from the 2nd column. Since it is in base 2 any number borrowed is 2. So borrowing two from the second will give (2 + 0) – 1 = 1
2nd Column: This reduces 0 to -1 in the second column. -1 is smaller than 1 so we have to borrow again from the third column. We now have:
= 2 + (- 1) – 1
= 1 -1
= 0
3rd Column: This also reduces 0 to – 1 in the 3rd column. This too is smaller than 1 so like the second column what we have is 2 – 1 – 1 = 0
4th Column: This reduces 1 to 0 in the fourth column. We then have 0 – 0 = 0
5th Column: This column requires no borrowing since 1 is greater than 0. We simply have 1 – 0 = 1
This yields 10001two
2. 20204six – 5125six
Solution
You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!
Click on the button "Subscribe Now" below for Full Access!
Subscribe Now
Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!



Responses