-
Number Base System I | Week 16 Topics2 Quizzes
-
Number Base System II | Week 23 Topics
-
Number Base System III | Week 32 Topics1 Quiz
-
Modular Arithmetic I | Week 42 Topics
-
Modular Arithmetic II | Week 53 Topics
-
Modular Arithmetic III | Week 64 Topics1 Quiz
-
Indices I | Week 73 Topics1 Quiz
-
Indices II | Week 81 Topic1 Quiz
-
Logarithms I | Week 93 Topics
-
Logarithms II | Week 104 Topics1 Quiz
Topic Content:
- Division of Number Bases
- Long Division Method
- Alternative Method
Example 2.2.1:
Divide the following numbers:
a. 1110two ÷ 111two
b. 1010two ÷ 10two
c. 1101001two ÷ 101two
Solution
The long division method is one of the most efficient and easiest ways to solve binary division.
Remember these rules
- The dividend is divided by the divisor, and the answer is the quotient.
- Compare the divisor to the first digit in the dividend. If the divisor is the larger number, keep adding digits to the dividend until the divisor is the smaller number. (For example, if calculating 156 ÷ 2, we would compare 2 and 1, note that 2 > 1, and compare 2 to 15 instead.)
a. 1110two ÷ 111two
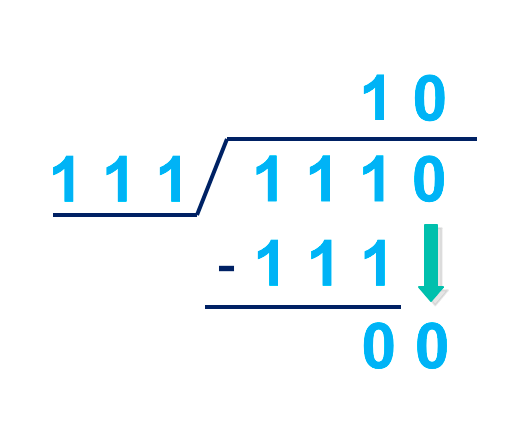
Explanation
111 is the divisor, 1110 is the dividend.
Compare the divisor (111) to the dividend (1110) from the first digit.
111 > 1 so we carry on (or add a 0)
111 > 11 so we carry on (or add a 0)
111 = 111, This can be divided. We write 1 in the quotient.
Like standard division, we then multiply the divisor (111) by 1 and then find the remainder by subtracting the result.
The remainder is 0 and the number brought down is 0. What we have now is 00.
We then try and divide again. 111 > 00 so we add a 0 to the quotient.
0010two = 10two
Answer = 10two
b. 1010two ÷ 10two
Answer = 101two
c. 1101001two ÷ 101two
Answer = 10101two
Example 2.2.2:
(i) \( \scriptsize 1111.01_2 \div 1101_2 \)
(ii) \( \scriptsize 242_5 \div 14_5 \)
(iii) \( \scriptsize 83A6{16} \: \div \: 6_{16} \)
In Binary Division, another method you can use is to first convert to base 10, do the division, and then convert the answer to the given base.
(i) \( \scriptsize 1111.01_2 \div 1101_2 \)
Solution
convert to base 10
i.e. \( \scriptsize 1111.01_{2} \\ \scriptsize = 1 \: \times \: 2^3 \:+\: 1 \:\times\: 2^2 \:+ \:1 \: \times \: 2^1 \: +\: 1 \: \times \: 2^0 \\ \scriptsize \: + \: 0 \: \times \: 2^{-1}\: + \: 1 \: \times\: 2^{-2}\)
⇒ \( \scriptsize 8 \: + \: 4 \: + \: 2 \: + \: 1 \: + \: 0 \: + \: 0.25 = 15.25 \)
\( \scriptsize 1101_{2} \\ \scriptsize = 1 \:\times \: 2^3 \: + \: 1 \: \times\: 2^2 \: + \: 1 \: \times \: 2^1 \: + \: 1 \: \times \: 2^0 \)⇒ \( \scriptsize 8 \: + \: 4 \: + \: 2 \: + \: 1 = 13 \)
∴ \( \scriptsize 1111.01_2 \div 1101_2 \equiv 15.25 \div 13 \)
= \( \scriptsize 1.173 \)
Convert 1.173 to base 2
Whole number part = 1
⇒ 0.173 = 0.0012
Therefore, \( \scriptsize 1.173 = 1.001_2 \)
(ii) \( \scriptsize 242_5 \div 14_5 \)
Solution
First, convert the given numbers to base 10.
⇒ \( \scriptsize 2\: \times \: 5^2 \: +\: 4 \: \times \: 5^1 \: + \: 2 \: \times \: 5^0 = 72_{10}\)
⇒ \( \scriptsize 1 \:\times \:5^1 \:+ \:4 \:\times\: 5^0 = 9_{10} \)
⇒ \( \therefore \frac {72_{10}}{9_{10}} \scriptsize = 8_{10} \)
We then convert 810 back to base 5
Therefore, \( \scriptsize 8_{10} = 13_{5} \)
(iii) \( \scriptsize 83A6_{16} \: \div \: 8_{16} \)
Solution
Convert both numbers to base 10
\( \scriptsize 83A6_{16} \: \div \: 8_{16} \\ \scriptsize = 8 \: \times \: 16^3 \: + \: 3 \: \times \: 16^2 \: + \: 10 \: \times \: 16^1 \: + \: 6 \: \times \: 16^0 \\ \scriptsize = 32768 \: + \: 768 \: + \: 160 \: + \: 6 \\ \scriptsize = 33,702\) \( \scriptsize 8_{16} \\ \scriptsize = 8 \: \times \: 16^0 \\ \scriptsize = 8 \: \times \: 1 \\ \scriptsize = 8 \)i.e \( \scriptsize 83A6_{16} \: \div \: 8_{16} \equiv 33,702 \: \div \: 8 \\ \scriptsize = 4212.75 \)
Convert back to base 16
Whole number part
Decimal part
Whole number part = \( \scriptsize 1074 \)
Decimal part = \( \scriptsize C \)
\( \scriptsize \therefore \: Answer = 1074.C_{16} \)
This is cool.
Easy to understand ☺️
pls how did you get 1.173 in example 2 question i ???
(1111.01 ÷ 1101) convert to base 10
= 15.25 ÷ 13 = 1.173
Thanks