Topic Content:
- To bisectBisect means dividing into two equal parts. It means to divide a geometric figure such as a line, an angle or any other shape into two congruent parts (or two parts... More a given line: To divide a line into two equal parts
- To bisect an angle: To divide an angle into two equal parts
- To copy an angle: To draw an angle similar to it
- Constructing Perpendiculars
- To construct an angle of 45°
- To construct an angle of 60°
- To construct an angle of 30°
- To construct an angle of 120°
- To construct an angle of 105o
- To construct an angle of 75°
- To construct angle 135°
- To construct angle 150°
1. To bisect a given line: To divide a line into two equal parts
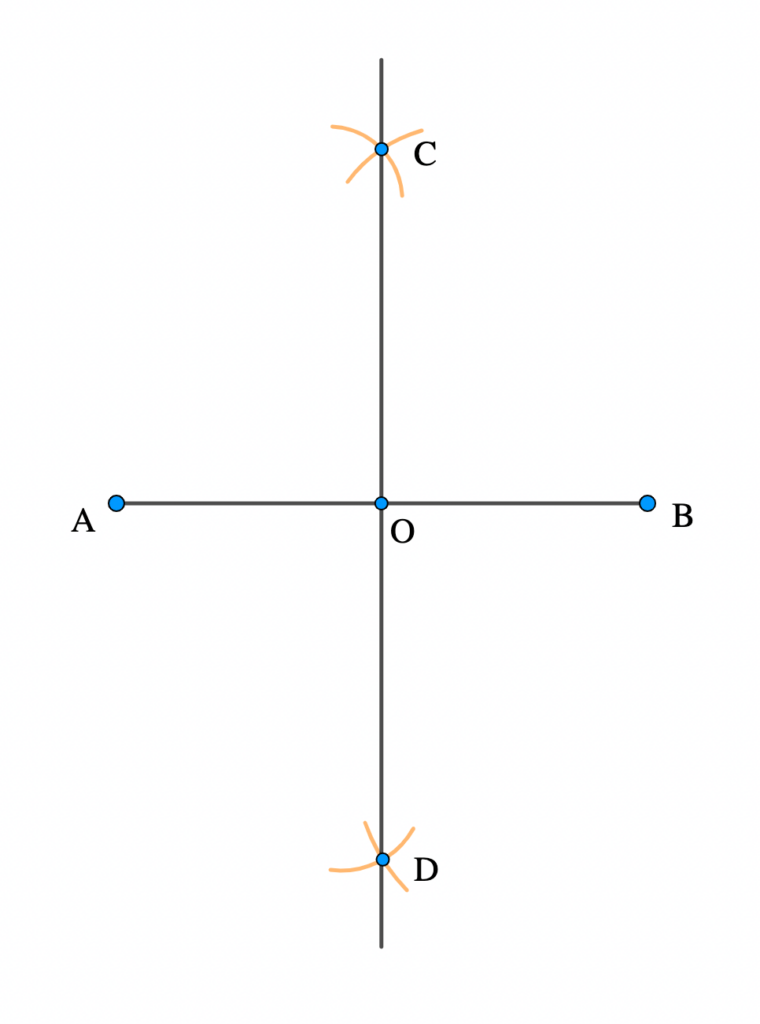
i. Draw a line AB (e.g. AB = 10 cm)
ii. Open your compass to a radius greater than half AB. Place the point of your compass on A and draw arcs above and below line AB.
iii. With centre B, using the same radius, draw arcs above and below line AB to cut the first two arcs at C and D.
iii. Draw a line to join C and D. Label the point where this line cuts AB as O. Since the line CD bisects AB at a right angle, CD is called the perpendicular bisector of AB, and point O is the mid-point of PQ.
You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!
Click on the button "Subscribe Now" below for Full Access!
Subscribe Now
Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!



Responses