Topic Content:
- Implication
- Simple Statement
- Compound Statement
Introduction:
To understand the concept of logical implication, we need to bring to bear our understanding of logical statements.
Recall, a statement could either be true or false. If statements X and Y are true, then the combination of X and Y is called implication.
Simple Statement:
This contains a single preposition or idea.
Compound Statement:
A compound statement contains two or more sub-statements. In practice, statements are usually more complex e.g. “Some graduates in Nigeria are employed and some are unemployed” This is an example of a compound statement. Since it contains a number of simple sub-statements:
Ɛ: Graduates who are in Nigeria
X: Graduates in Nigeria who are employed
~X: Graduates in Nigeria who are unemployed
The Venn diagram below illustrates the given statements.
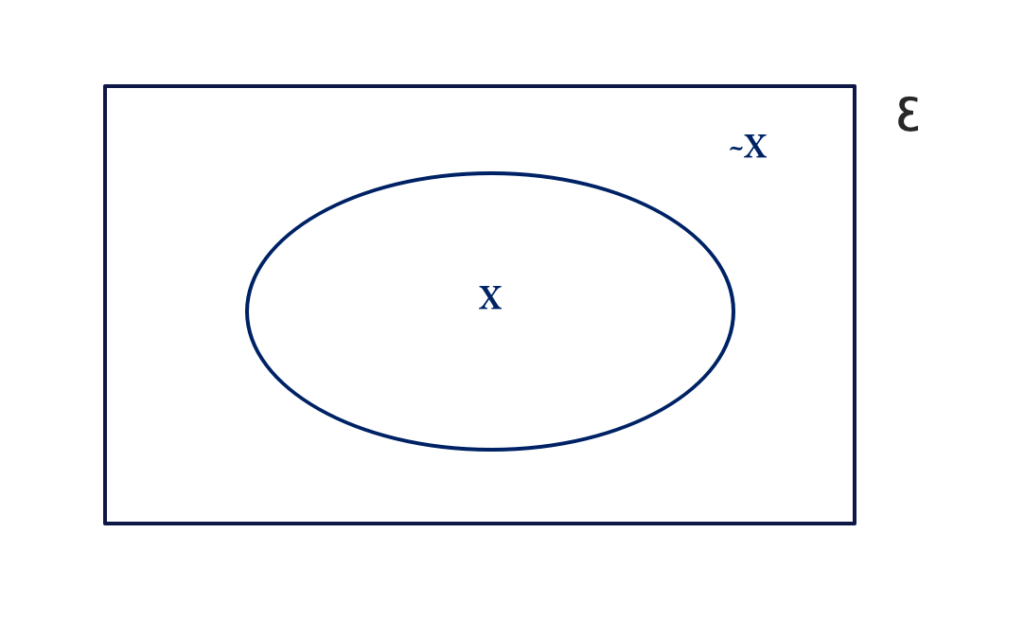
Recall that ~X and X′ both mean the complement of set X. Note also that Venn diagrams are very useful for showing compound statements. Consider the Venn diagram below:
You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!
Click on the button "Subscribe Now" below for Full Access!
Subscribe Now
Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!



Responses