Angular Speed and Velocity

When a stone is tied to the end of a string or rope and whirled around, the stone moves in a circular path as shown in the diagram below.

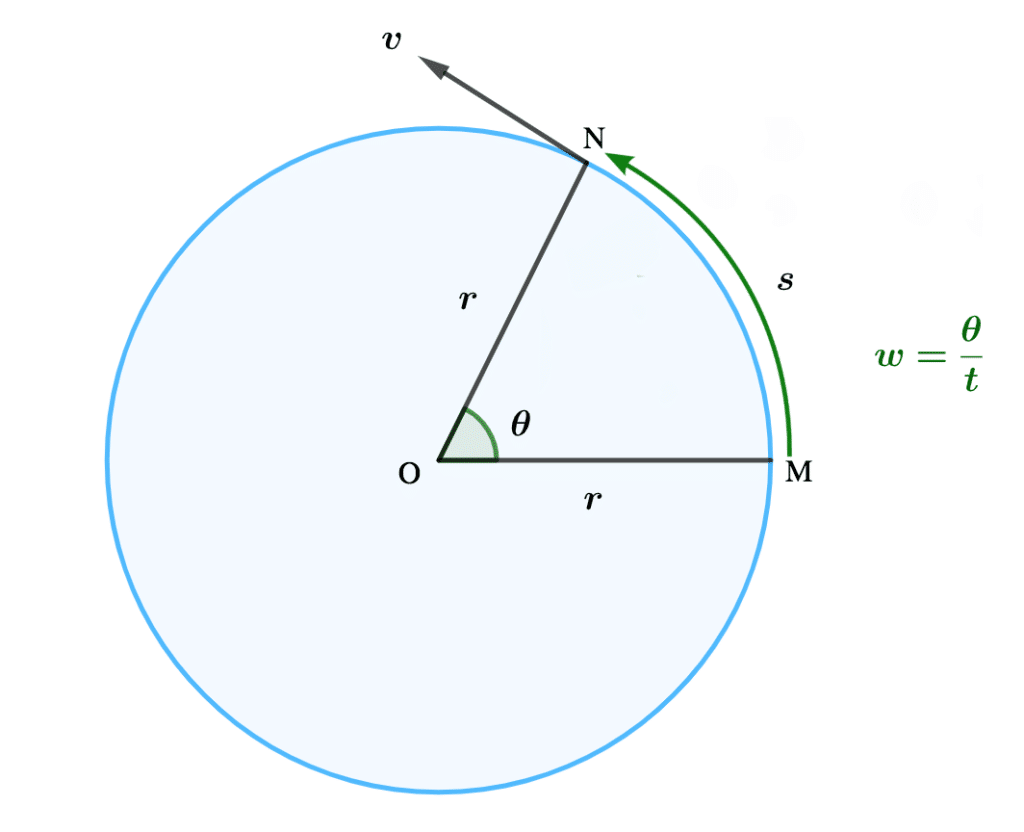
Suppose that as the stone is being whirled around, it moves from point M to N, in t seconds, so that the radius OM sweeps through an angle θ at the same time.

As the stone moves around the circular path and sweeps through angle θ, the stone moves with angular velocity, \(\scriptsize \omega \)

Angle \(\scriptsize \hat{MON} = \theta ,\) the angular velocity of motion, \( \scriptsize \omega \) can be defined as;

\(\scriptsize \omega = \normalsize \frac{\theta}{t}\) ……………..(1)

We can say that the angular velocity, \(\scriptsize \omega , \) is the angle turned through, with respect to time.

Recall that linear velocity, v is given by the formula:

\( \scriptsize v = \normalsize \frac{s}{t} \) …………….(2)

where s is the length of the arc MN.

Comparing equations 1 and 2, instead of using linear displacement in 1, we used angular displacement θ.

The image illustrates the relationship between the radius and the central angle θ in radians.

We define the rotation angle θ to be the ratio of the arc length to the radius of curvature: