Topic Content:
- Meaning of Friction
- Laws of Solid Friction
- Coefficient of Friction
- Relationship Between Friction Force, Normal Reaction and Coefficient of Friction
What is Friction?
Friction is the opposing force between two surfaces in contact when they move over one another.
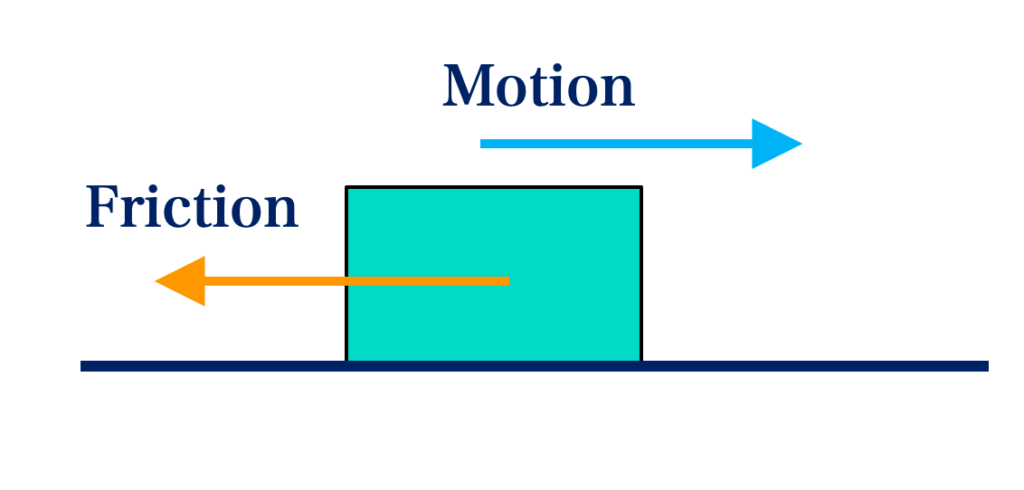
There are two types of friction namely:
Static or Limiting Friction: This is the maximum force that must be overcome before a body can just start to move over another.
Kinetic Friction: This is the force needed to keep an object moving at uniform speed.
A larger force is always required to move a static object than to keep an object moving, hence static friction is greater than kinetic friction.
Laws of Solid Friction:
1. Friction opposes motion.
2. Friction is directly proportional to the normal frictional force.
3. Frictional force is directly proportional and perpendicular to the normal reaction.
4. Friction is independent of the area of surfaces in contact.
5. Friction depends on the nature of surfaces in contact.
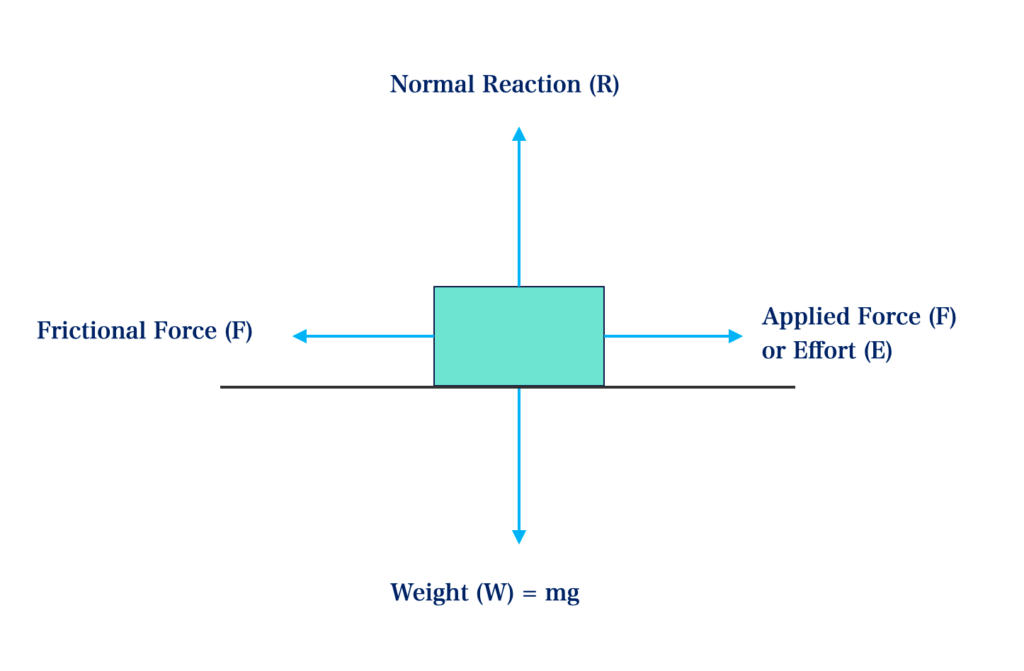
Coefficient of Friction:
You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!
Click on the button "Subscribe Now" below for Full Access!
Subscribe Now
Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!



Responses