Mechanical Energy Transformation | Law of Conservation of Energy
Topic Content:
- Law of Conservation of EnergyEnergy is the ability to do work. Energy exists in several forms such as heat, kinetic or mechanical energy, light, potential energy, and electrical energy. Units of Energy: The SI unit... More
- Potential and Kinetic Energy of a Falling Body
- Potential and Kinetic Energy of a Simple Pendulum
Energy can be transformed from one form to another e.g. potential energy can be converted to kinetic energy and vice versa.
Law of Conservation of Energy:
The law of conservation of energy states that in an isolated or closed system, the total energy remains constant, in other words, energy can neither be created nor destroyed, but it can be transformed from one form to another.
Electrical energy can be converted to heat energy and light energy. Mechanical energy can be converted to heat energy and chemical energy can be converted to food energy or light energy.
By an isolated system, we mean a group of objects that neither receives energy from nor gives energy to objects outside the system.
Potential and Kinetic Energy of a Falling Body:
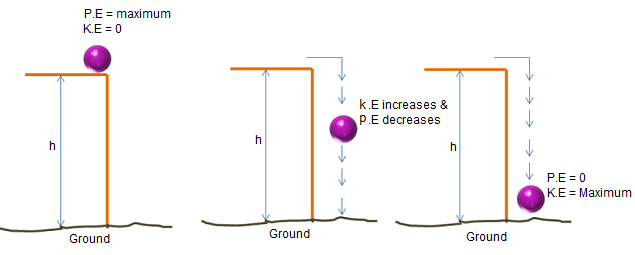
Let’s refer to kinetic energy as Ek and potential energy as Ep.
An object of mass m, held at point h, possesses maximum potential energy, Ep, and kinetic energy, Ek, is zero, because of no movement.
You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!
Click on the button "Subscribe Now" below for Full Access!
Subscribe Now
Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!



Responses