Back to Course

SS2: MATHEMATICS - 1ST TERM

0% Complete
0/0 Steps
  1. Trigonometry III | Week 1
    1 Topic
    |
    1 Quiz
  2. Mensuration II | Plane Shapes | Week 3
    2 Topics
    |
    1 Quiz
  3. Mensuration III | Solid Shapes | Week 4, 5, 6
    4 Topics
    |
    1 Quiz
  4. Logarithms of Numbers Less Than One | Week 7
    2 Topics
  5. Theory of Logarithms | Week 8
    6 Topics
    |
    1 Quiz
  6. Approximation & Accuracy | Week 9
    5 Topics
    |
    1 Quiz

Quizzes




  • Kofa Study
Lesson Progress
0% Complete

Topic Content:

  • Special Angles

Consider an Isosceles right-angled triangle of equal sides of 1 unit each and hypotenuse side \( \scriptsize \sqrt {2}\) units.

Screenshot 2023 10 16 at 05.31.59

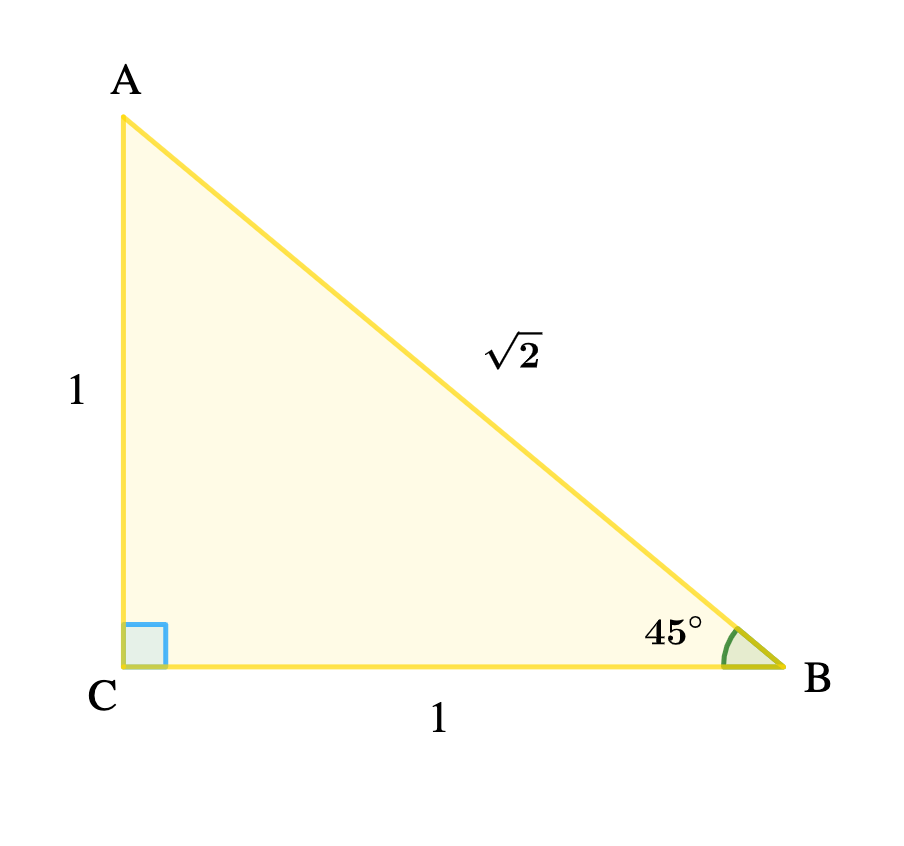
sin 45° = \( \frac {1}{\sqrt {2}}\)

cos 45° = \( \frac {1}{\sqrt {2}}\)

tan 45° = \( \frac {1}{1} = \scriptsize 1\)

30o and 60o

Consider an equilateral ∆ of side 2 units.

Screenshot 2023 10 16 at 05.46.41

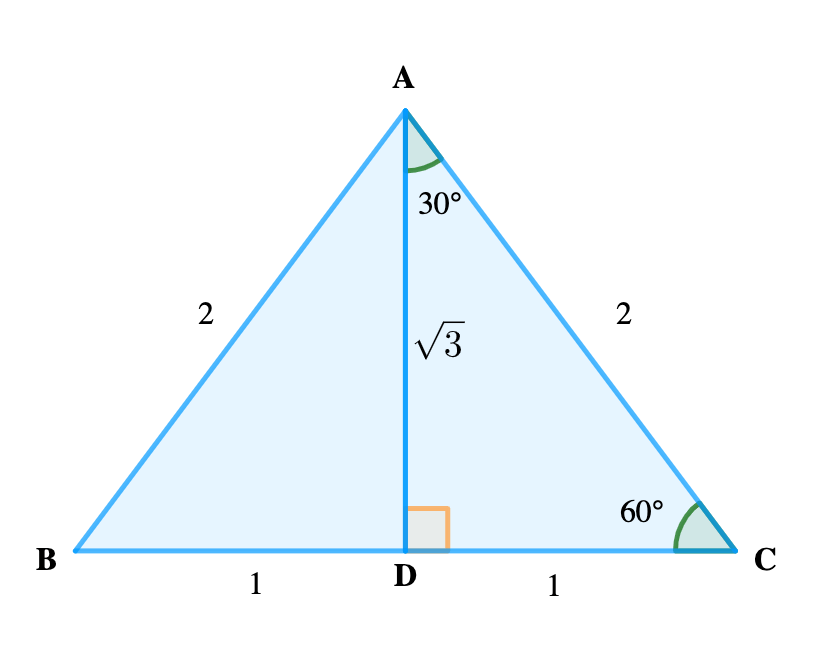
sin 30° = \( \frac {1}{2}\)

cos 30° = \( \frac {\sqrt {3}}{2}\)

tan 30° = \( \frac {1}{\sqrt {3}}\)

sin 60° = \( \frac {\sqrt {3}}{2}\)

cos 60° = \( \frac {1}{2}\)

tan 60° = \( \frac {\sqrt {3}}{1}\)

Recall,

1) sin 45o = cos 45o = \( \frac {1}{\sqrt {2}}\)

2) sin 30o = cos 60o = \( \frac {1}{2}\)

3) sin 60o = cos 30o = \( \frac {\sqrt {3}}{2}\)

4) tan 30o = \( \frac {1}{tan 60°}\)

Example 1.1.1:

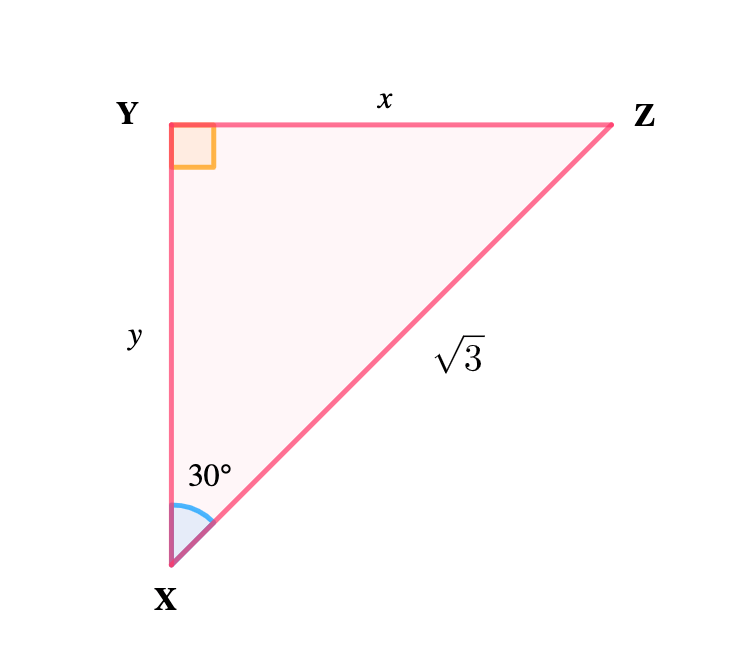
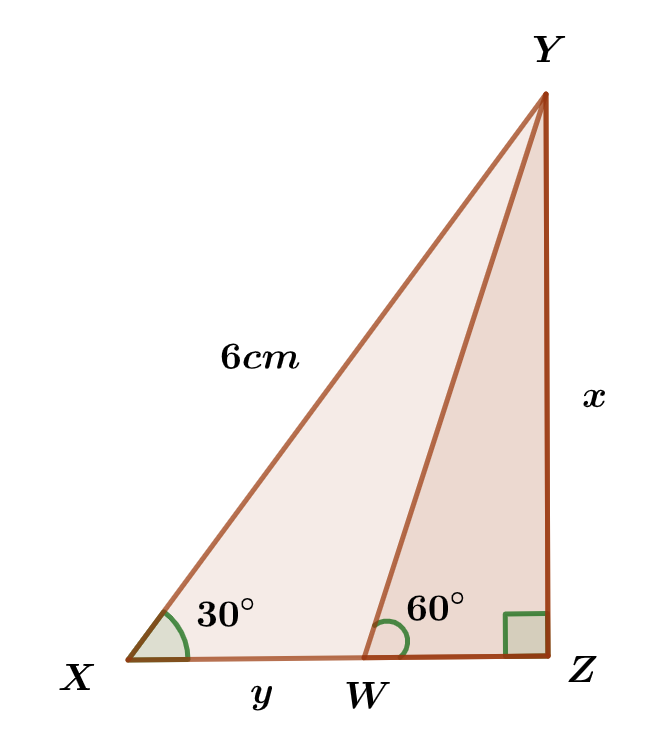
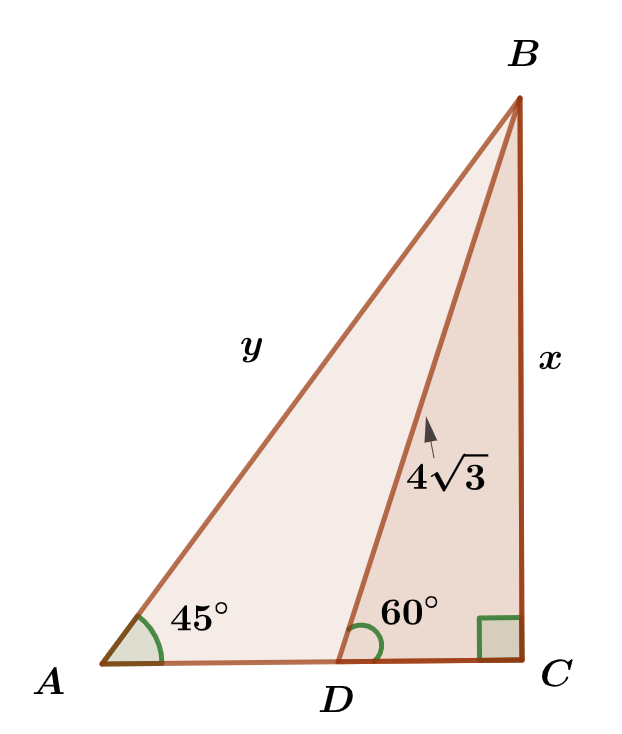
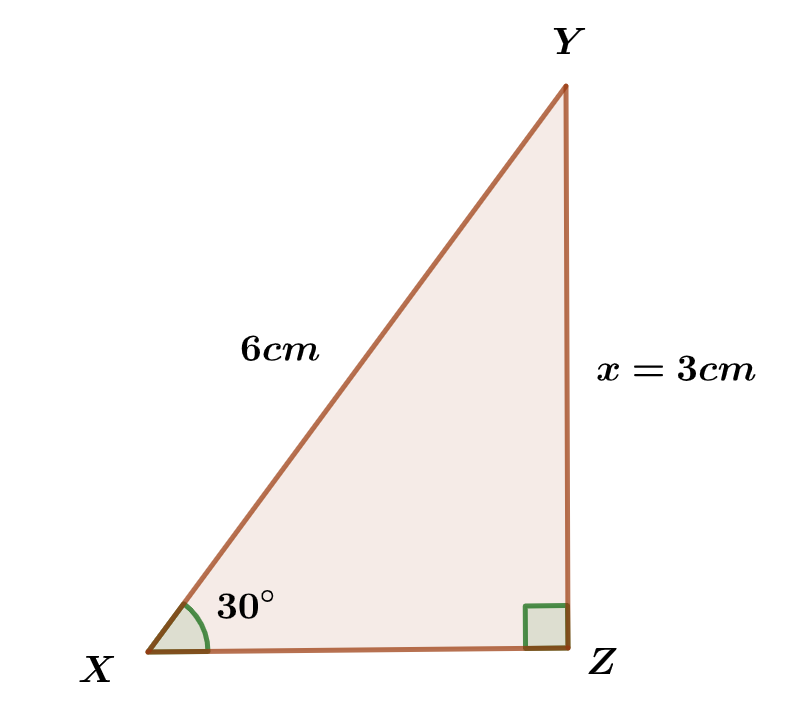
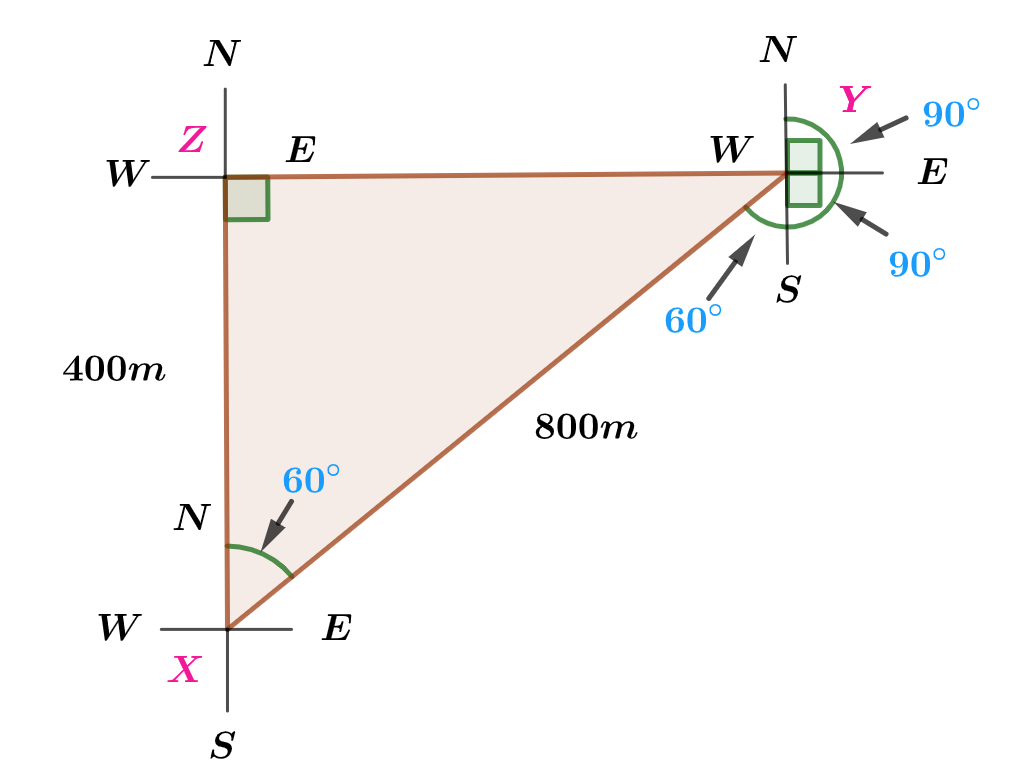
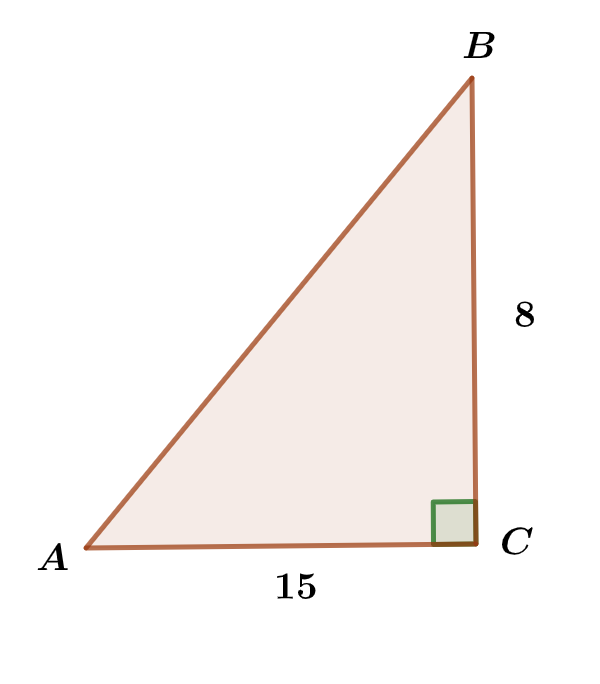
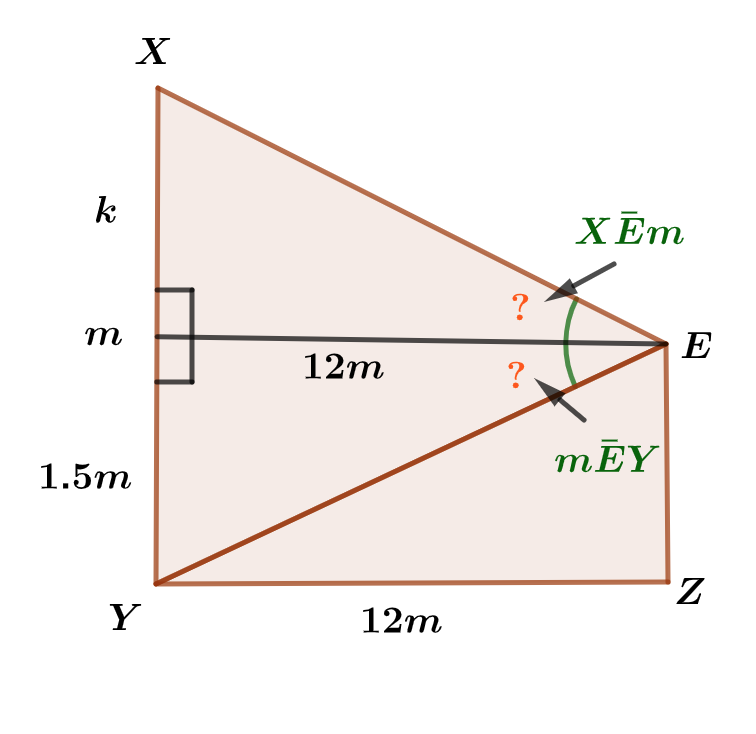
In the figures in a, b and c below, find the lengths Marked x and y.

(a)

Screenshot 2023 10 16 at 05.55.26
View Solution

(b)

Screen Shot 2021 11 22 at 9.31.55 AM
View Solution

(c)

Screen Shot 2021 11 22 at 12.43.00 PM
View Solution

Example 1.1.2:

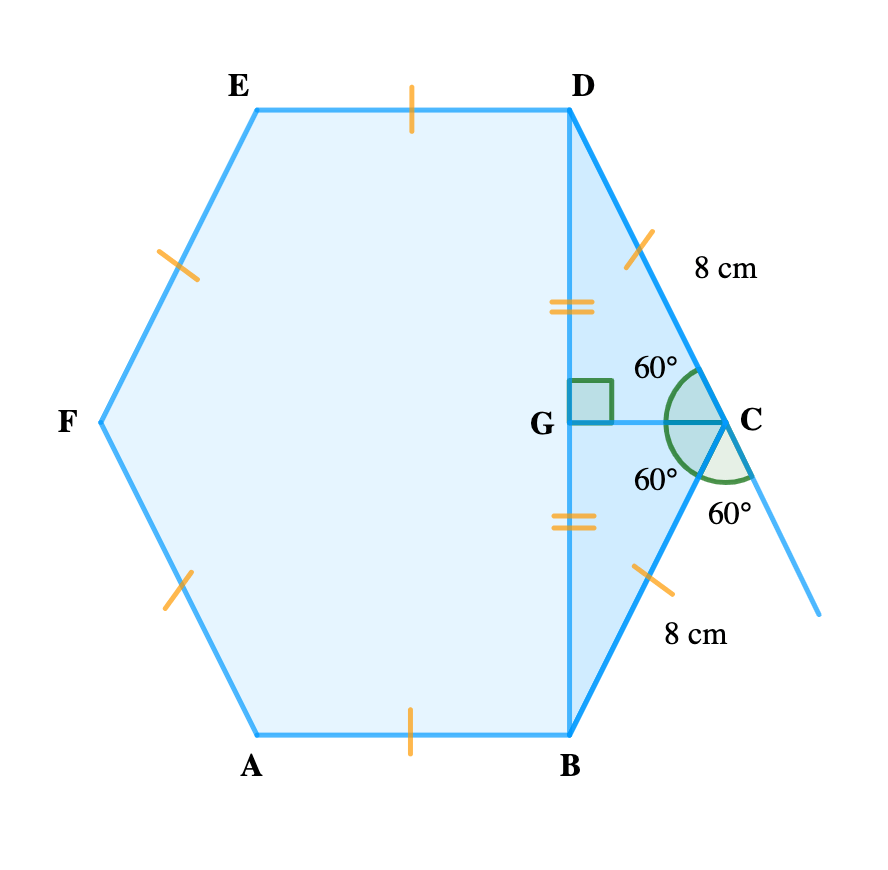
A regular hexagon has sides of length 8 cm. Find the perpendicular distance between two opposite faces.

 

You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!

Click on the button "Subscribe Now" below for Full Access!

Subscribe Now

Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!

avataravataravataravataravatar

Responses

Your email address will not be published. Required fields are marked *

SOLUTION (a)

Note: We are looking for small letters x and y

Solution:

First, find x

YZ = opposite = x

XZ =  √3 = hypotenuse

θ =  30°

sin 30° = \( \frac {opp}{hyp} = \frac {YZ}{XZ} = \frac {x}{\sqrt {3}}\)

\( \frac {1}{2} =  \frac {x}{\sqrt {3}} \\ \frac {x}{\sqrt {3}} = \frac {1}{2} \\ \)

Multiply both sides by √3

⇒ \( \frac {x}{\sqrt {3}} \scriptsize \; \times \;  \sqrt {3} = \normalsize \frac {1}{2}  \scriptsize \; \times \;  \sqrt {3} \)

⇒ \(\scriptsize \therefore x =  \normalsize \frac{\sqrt {3}} {2} \)

Then find y,

XY = adjacent = y

XZ =  √3 = hypotenuse

θ =  30°

We know the adjacent and hypotenuse so we use cos

cos 30° = \( \frac {adj}{hyp} = \frac {XY}{XZ} \\  \scriptsize cos 30^{\circ} = \normalsize \frac {y}{\sqrt {3}} \)

Remember,

cos 30° = \( \frac {\sqrt {3}}{2}\)

substitute cos 30° into the equation

∴ \( \frac {\sqrt {3}}{2} = \frac {y}{\sqrt {3}} \)

move the unknown y to the left-hand side

∴ \(  \frac {y}{\sqrt {3}} = \frac {\sqrt {3}}{2} \)

Multiply both sides by √3

∴  \( \frac {y}{\sqrt {3}} \scriptsize\; \times \;  \sqrt {3} = \normalsize\frac {\sqrt {3}}{2} \scriptsize\; \times \;  \sqrt {3} \)

∴  \( \scriptsize y = \normalsize\frac {\sqrt {3} \; \times \; \sqrt {3}}{2} \)

⇒ \( \scriptsize y = \normalsize\frac {3}{2} \)

or

\( \scriptsize y = 1\normalsize\frac {1}{2} \)

SOLUTION (b)

Note: We are looking for small letters x and y

To find x we use \( \scriptsize \bar {ZXY} \)

YZ = opposite = x

XY =  6cm = hypotenuse

θ =  30°

sin 30° = \( \frac {opp}{hyp} = \frac {YZ}{XY} = \frac {x}{6}\)

⇒ \( \frac {1}{2} =  \frac {x}{6}\)

move the unknown x to the left-hand side

⇒ \( \frac {x}{6} =  \frac {1}{2}\)

Multiply both sides by 6

⇒ \( \frac {x}{6}  \scriptsize \: \times \: 6 =  \normalsize \frac {1}{2} \scriptsize \: \times \: 6 \)

x = \( \frac {6}{2}\)

∴  x = 3 cm

 

To find y we have to first find XZ then WZ then subtract.

∴ y = XZ – WZ

First, find XZ

To find XZ we use \( \scriptsize \bar {ZXY} \)

XZ =  Adjacent

YZ  = x = 3cm = Opposite

θ =  30°

tan 30° = \( \frac {opp}{adj} =  \frac {YZ}{XZ} \)

tan 30° = \( \frac {x}{XZ}  \)

Remember tan 30° = \( \frac {1}{\sqrt{3}}\)

x = 3cm

⇒ \( \frac {1}{\sqrt{3}} =  \frac {3}{XZ} \)

move the unknown XZ to the left-hand side

⇒ \(  \frac {3}{XZ} = \frac {1}{\sqrt{3}} \)

Cross multiply

⇒ \(  \scriptsize XZ  = 3 \sqrt{3} \: cm\)

 

The next step is to find WZ

To find WZ we use \( \scriptsize \bar {ZWY} \)

Adjacent = WZ

Opposite = x = 3cm (solved previously)

θ =  60°

∴ tan θ = \( \frac {opp}{adj} \)

∴ tan 60° = \( \frac {3}{WZ} \)

Remember tan 60° = \( \frac {\sqrt{3}}{1} \)

∴ \( \frac {\sqrt{3}}{1} = \frac {3}{WZ}  \)

Cross multiply

⇒ \( \scriptsize WZ \sqrt{3} = 3 \)

Divide both sides by √3

⇒ \( \frac{WZ \sqrt{3}}{\sqrt{3}} = \frac{3}{\sqrt{3}}  \)

∴ \( \scriptsize WZ  = \normalsize \frac{3}{\sqrt{3}}  \)

Therefore, y = XZ – WZ

⇒ \(  \scriptsize XZ  = 3 \sqrt{3} \)

⇒ \( \scriptsize WZ = \frac{3}{\sqrt{3}}  \)

y = \(  \scriptsize  3 \sqrt{3} \: – \:  \normalsize \frac{3}{\sqrt{3}} \)

y = \( \frac { 3 \sqrt{3} \: \times \: \sqrt{3} \:   – \: 3}{\sqrt{3}} \)

y = \( \frac { 3  \: \times \:  3 \:  – \: 3}{\sqrt{3}} \)

y = \( \frac { 9 \:  – \: 3}{\sqrt{3}} \)

y = \( \frac {6}{\sqrt{3}} \)

SOLUTION (c)

 

Find small letters x and y

To find x we use the triangle \( \scriptsize \bar {CDB} \)

BC = x = opposite

BD = 4√3 = hypotenuse

CD = adjacent

θ = 60°

sin 60° = \( \frac {opp}{hyp} \\ =\frac {BC}{BD} \\ = \frac {x}{4 \sqrt{3}}\)

Remember sin 60° = \( \frac{\sqrt{3}}{2} \)

∴ \( \frac {\sqrt{3}}{2} =  \frac {x}{4 \sqrt{3}}\)

Cross Multiply

⇒ \( \scriptsize x = \normalsize \frac {4 \sqrt{3} \; \times \sqrt{3} }{2} \)

⇒ \( \scriptsize x = \normalsize \frac {2 \sqrt{3} \; \times \sqrt{3} }{1} \)

i.e. x = 2 × 3

Hence, x = 6cm

 

To find y use the triangle \( \scriptsize \bar {CAB} \)

BA = y = hypotenuse

BC = x = 6cm = opposite

θ = 45°

sin 45° = \( \frac {opp}{hyp} =\frac {BC}{BA} \\= \frac {x}{y}\\ = \frac {6}{y} \)

Remember Sin 45° = \( \frac {1}{\sqrt{2}}\)

⇒ \( \frac {1}{\sqrt{2}} =  \frac {6}{y}\)

Cross Multiply

⇒ \( \scriptsize y = 6 \sqrt {2} cm \)

SOLUTION (Example 2)

The perpendicular distance between the two faces is BD. We therefore have to find the length of DB

We also know DB = 2 DG

or DB = 2 BG

or DB = DG + BG

This is because DG and BG have the same value

The first step is to find DG which is \( \frac{1}{2}\) of BD

sin 60° = \( \frac {opp}{hyp} = \frac {DG}{DC} = \frac {DG}{8}\)

sin 60° = \( \frac {\sqrt{3}}{2} \)

∴ \( \frac {\sqrt{3}}{2} =  \frac {DG}{8}\)

⇒ \( \scriptsize DG = \normalsize \frac {8 \sqrt{3} }{2} \)

⇒ \( \scriptsize DG = 4 \sqrt{3} \)

DB = 2DG

= \( \scriptsize 2 \: \times \: 4  \sqrt{3} \)

DB = \( \scriptsize 8  \sqrt{3} \)

SOLUTION (Example 3)

Question

From a place 400 m north of X, a student walks eastwards to a place Y which is 800 m from X. What is the bearing of X from Y? (WAEC)

Solution

Let’s call the place where the students start to walk from Z. Z is north of X so XZ is a straight line upwards. XZ = 400 m

He then walks Eastward to place Y. Y is 800 m from X so we connect the line between X and Y and write 800 m next to it.

 

We know XZ = 400 m and XY is 800 m. The question is asking for the bearing of X from Y which is the angle shown in the diagram below. You can see that we named two angles  \( \scriptsize \bar {YXZ}  \) because they are alternate angles and are equal.

So first, we calculate \( \scriptsize \bar {YXZ}  \), and then we will be able to calculate the bearing of X from Y.

So from the diagram below, we can calculate \( \scriptsize \bar {YXZ}  \)

⇒ \( \scriptsize \bar {YXZ} = \theta \)

Adjacent = 400 m

Hypotenuse = 800 m

⇒ \(\scriptsize cos \theta =  \normalsize \frac {adj}{hyp} \\ = \frac {400}{800}\)

cos θ = (0.5000) = \( \frac{1}{2} \)

but cos 60° = \( \frac{1}{2} \)

∴ θ = 60°

⇒ \( \scriptsize \bar {YXZ} = 60^{/circ} \)

 

We can then redraw the diagram as shown below.

The bearing of X from Y = (90° + 90° + θ)

Y = (90° + 90° + 60°)

= 180° + 60°

= 240°

SOLUTION (Example 4)

Question

If tan θ = \( \frac{8}{15} \),    find the value of \( \frac{sin \theta \: +\: cos \theta}{Cos \theta(1\: – \: Cos \theta)} \)

Solution

If tan θ = \( \frac{8}{15} \)

We can draw a right-angle triangle from this information because

tan θ = \( \frac{opp}{adj} \)

8 = opposite, 15 = adjacent

Using Pythagoras Theorem

⇒ \( \scriptsize AB = \sqrt {8^2 + 15^2} \)

⇒ \( \scriptsize AB = \sqrt {289} = 17cm \)

considering the angle \( \scriptsize \bar{CAB} = \theta \)

adjacent =  AC = 15

hypotenuse = AB =  17

opposite =  CB = 8

cos θ° = \( \frac {adj}{hyp}\\ = \frac {AC}{AB}\\ = \frac {15}{17}\)

sin θ° = \( \frac {opp}{hyp} \\ = \frac {CB}{AB}\\ = \frac {8}{17}\)

 

Substitute these values into the given equation

⇒ \( \frac{sin \theta \: +\: cos \theta}{Cos \theta(1\: – \: Cos \theta)} \)

⇒ \( \frac{sin \theta \: +  \: cos\theta }{Cos \theta (1\: -\: Cos \theta)} \\ =  \large \frac {\frac {8}{17} \: + \:  \frac {15}{17}}{\frac {15}{17} \left ( \scriptsize 1 \: –  \: \normalsize \frac {15}{17}  \right )}  \)

= \( \large \frac { \frac{23}{17}}{\frac {15}{17} \left (  \frac {17 \: -\: 15}{17}  \right )}  \)

= \( \large \frac { \frac{23}{17}}{\frac {15}{17} \left (  \frac {2}{17}  \right )}  \)

= \( \large \frac { \frac{23}{17}}{\frac {30}{289}}  \)

= \(  \frac{23}{17}  \:  \times \:  \frac {289}{30} \)

= \(  \frac{23}{1} \:  \times \: \frac {17}{30} \)

= \(  \frac{391}{30} \scriptsize \:  0r \: 13 \normalsize \frac {1}{30} \)

SOLUTION (Example 5)

Question

A vertical pole, XY is erected on a piece of level ground. A student whose eye is 1.5 m above the ground is standing at Z, 12 m away from Y, the foot of the pole. If XEY = 50º, calculate the height of the top of the pole above the ground level. Give your answer correct to the nearest metre.

Solution

 

The height of the Pole = XY

eye is 1.5 m from ground

Study and make sure you understand the diagram.

mY + mX = XY

mY = 1.5 m

mX = k = ?

We need to find k in order to find XY

To find K we can use the angle  \(\scriptsize \bar{XEm} \)which is not given. The angle given in the question is \( \scriptsize \bar{XEY}  = 50^{/circ}\)

To find \(\scriptsize \bar{XEm} \) we need to first find \(\scriptsize \bar{mEY} \) then subtract this value from 50º

Triangle \(\scriptsize \bar{mEY} \)

θ = \(\scriptsize \bar{mEY} \)

opposite = mY = 1.5m

adjacent = mE = 12 cm

tan θ = \( \frac{opp}{adj} \\ = \frac{1.5}{12}\\ = \scriptsize 0.125 \)

tan θ = (0.125)

tan -1  θ  = 7.125016

θ = 7°

⇒ \(\scriptsize \bar{mEY} \) =  θ = 7°

⇒ \( \scriptsize X\bar{E}Y = X\bar{E}m \: + \: m \bar{E}Y \)

50° = XEm + 7°

XEm = 50 – 7

= 43°

We can then find k, now that we know \(\scriptsize \bar{XEm} \)

Triangle \(\scriptsize \bar{XEm} \)

opposite = mX = k

adjacent = mE = 12m

XEm = θ = 43°

tan 43° = \( \frac{opp}{adj} \\ = \frac{k}{12}  \)

⇒ \( \frac{k}{12} = \scriptsize tan 43^o  \)

k = 12 × tan 43º

=12 × 0.9325

k = 11.1901

Height of pole = XY

XY = mY + mX

XY =  1.5 + k

XY  = 1.5 + 11.11901

XY  = 12.69

XY  =12.7

Answer: XY  =13 m (nearest metre)

SOLUTION (Example 6)

Question

The shadow of a post is 6m longer when the elevation of the Sun is 30° than when it is 60°. Calculate the height of the post.

Solution

Consider  \( \scriptsize \Delta A\bar{C} B\)

opposite = AB = h 

Adjacent BC = x

θ = 60°

tan 60° = \( \frac{opp}{adj}  \)

tan 60° = \( \frac{h}{x}  \)

⇒ \( \frac{h}{x}  \) = tan 60°

cross multiply

i.e. h = x tan 60°

i.e. h = x √3 ……….. (i)

also consider \( \scriptsize \Delta A\bar{D} B\)

opposite = AB =  h

adjacent = BD = x + 6

θ = 30°

tan 30° = \( \frac{opp}{adj} \\ = \frac{h}{x + 6}  \)

tan 30° = \( \frac{1}{\sqrt{3}}  \)

∴ \( \frac{1}{\sqrt{3}} = \frac{h}{x + 6}   \)

cross multiply

x + 6 = h√3  ………. (ii)

Substitute for h (equation (i)) in equation (ii)

i.e. x + 6 =  x√3  × √3

x + 6 = 3x

i.e. 2x = 6

i.e. x = 3m

Substitute for x in equation (i)

i.e. h = x√3 , 

Answer:  h = 3√3 m

SOLUTION (Example 7)

Question

A man sets out to travel from A to C via B. From A he travels a distance of 8 km on a bearing N30ºE to B. From B he travels a further 6 km due east.

Solution

Special angle

(i) Calculate how far C is north of A

How far C is north of A is the line DA shown in the diagram above.

Using the triangle BAD in purple we can calculate DA

hypotenuse = 8km

adjacent = DA

θ = 30º

From the values, we can use cos

Cos θ = \( \frac {adj}{hyp} \)

Cos 30º = \( \frac {DA}{8km} \)

:> \( \frac {DA}{8km} \) = Cos 30º

DA = \( \scriptsize 8 \times  \normalsize \frac{\sqrt{3}}{2} \)

DA = 4√3

Answer: C is 4√3 km north of A

 

(ii) Calculate how far C is East of A.

How far C is east of A is the line CD shown in the diagram above.

CB + BD = CD

CB is given = 6 km, therefore we need to find BD

Using the triangle BAD in purple we can calculate BD

hypotenuse = 8 km

opposite = BD

θ = 30º

From the values, we can use sin

sin 30° = \( \frac{opp}{hyp} = \frac{BD}{8} \)

⇒ \( \frac{BD}{8} \) = sin 30°

BD = \( \scriptsize 8 \times  \normalsize \frac{1}{2} \)

BD = 4

CD = CB + BD

CB = 6km, BD = 4km

∴ CD = 6km + 4km

CD = 10km

 

 

2. Hence, or otherwise, calculate the distance AC correct to 1 decimal place.

Using Pythagoras Theorem

⇒ \(\scriptsize \bar{AC}^2 =  CD^2 + DA^2\)

CD = 6 km + 4 km = 10 km

DA = 4√3 km

AC = ?

⇒ \(\scriptsize \bar{AC} = \sqrt { 10^2 + (4 \sqrt {3})^2}\)

= \( \scriptsize \sqrt {100 + 48} = \sqrt {148} \)

= \( \scriptsize 2 \sqrt {37} = 12.1655 \)

Answer: \( \scriptsize \bar{AC} = 12.2km\)

Report

Harassment or bullying behavior
Contains mature or sensitive content
Contains misleading or false information
Contains abusive or derogatory content
Contains spam, fake content or potential malware

Block Member?

Please confirm you want to block this member.

You will no longer be able to:

  • See blocked member's posts
  • Mention this member in posts
  • Invite this member to groups
  • Message this member
  • Add this member as a connection

Please note: This action will also remove this member from your connections and send a report to the site admin. Please allow a few minutes for this process to complete.

Report

You have already reported this .
error: Alert: Content selection is disabled!!