Topic Content:
- Graphs of Quadratic Functions
The expression x2 + bx + c is called a quadratic function of x, where a, b and c are constants. When a quadratic function y = x2 + bx + c is plotted, its graph gives a smooth curve called a parabola.
Consider \( \scriptsize y = x^2 + bx + c\)
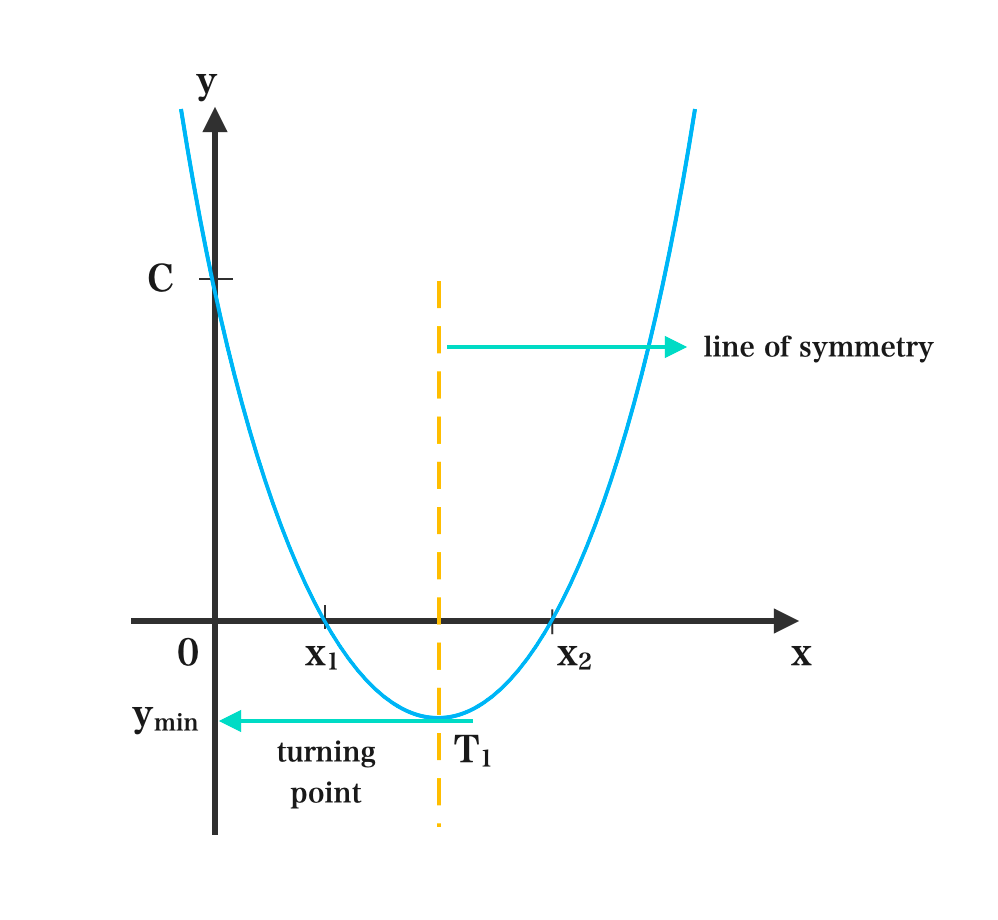
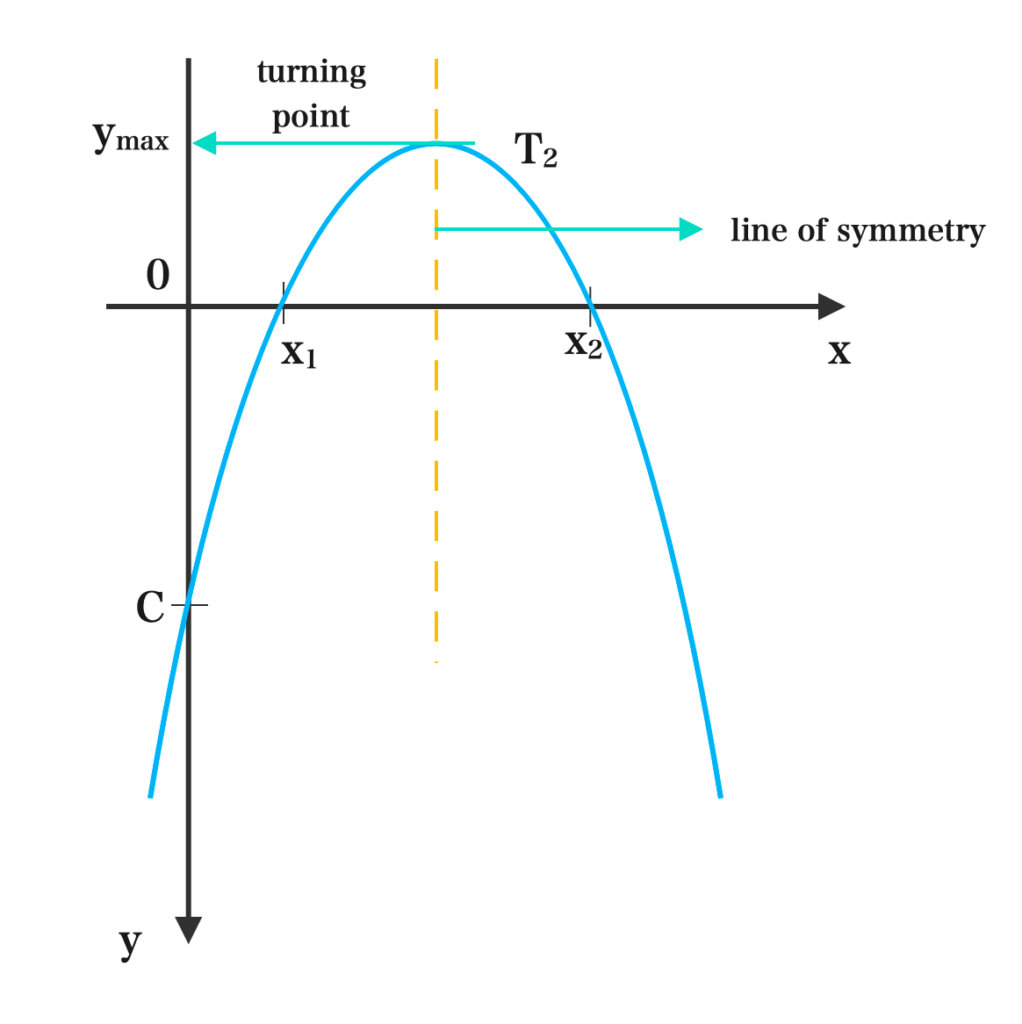
Also, we can have Consider \( \scriptsize y = -ax^2 + bx + c\)
Hint: The highest power of x is 2 i.e. a second degree function
- The points T1 and T2 are the turning points i.e. where the curve changes direction (inflexion point)
- When a is positive, we have a minimum curve with shape and the minimum value of the function ymin is at the turning point T1 and the value of x where it occurs gives the equation of the line of symmetryA line of symmetry is the line that divides a shape or an object into two equal and symmetrical parts. More.
- When a is negative, we have a maximum curve shape and the maximum value of the function ymax is at the turning point T2 and the value of x where it occurs gives the equation of the line of symmetry.
- The line of symmetry or the axis of symmetry divides the curve into two equal parts.
Example 7.1.1:
Plot the curve of y = x2 + x – 6 for values of x from -4 to 3
(a) Use the curve to find :
(i) the values of x when y = 2.8
(ii) the value of y when x = 1.4
(iii) the minimum value of the function and the value of x
(b) Draw the axis of symmetry of the curve and write down its equation
Solution:
You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!
Click on the button "Subscribe Now" below for Full Access!
Subscribe Now
Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!



Responses