Condition of Equilibrium Under the Action of Non-Parallel Coplanar Forces

The conditions of equilibrium under the action of non-parallel coplanar forces are:

1. Forces: The vector sum of all the forces acting on a body must be zero i.e. 

(i) The algebraic sum of the horizontal components must be zero i.e. ∑F_x = 0

(ii) The algebraic sum of the vertical components of the forces must be zero i.e.  ∑F_y = 0

2. Moments:  The algebraic sum of the moments of all the forces about any axis perpendicular to the plane of the forces must be zero.

Example 5.2.1:

In the diagram below an object of mass 500 kg is kept in equilibrium by three cables. Find the tension in each of the three cables. (g = 9.8 ms^-2)

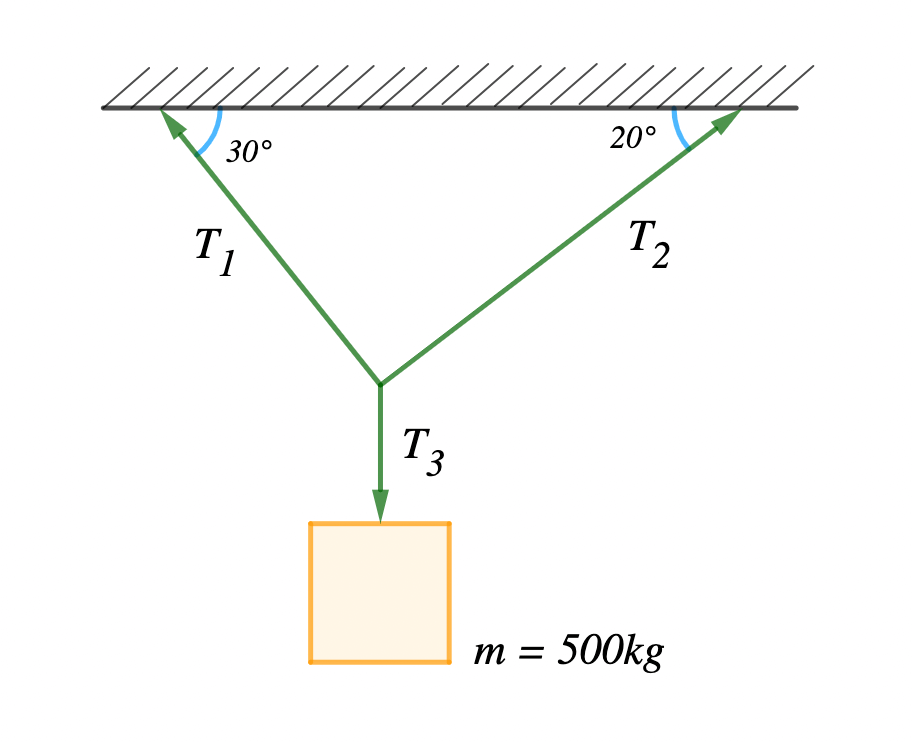
Solution:

Tension in cable 3 can be found easily

T₃ = mg

∴ T₃ = 500 × 9.8 = 4900 N (in the negative direction)

To find T₁ and T₂, since the object is in equilibrium ∑F_x = 0 and ∑F_y = 0

The horizontal component of T₁ = T_1X

The vertical component of T₁ = T_1Y

The horizontal component of T₂ = T_2X

The vertical component of T₂ = T_2Y

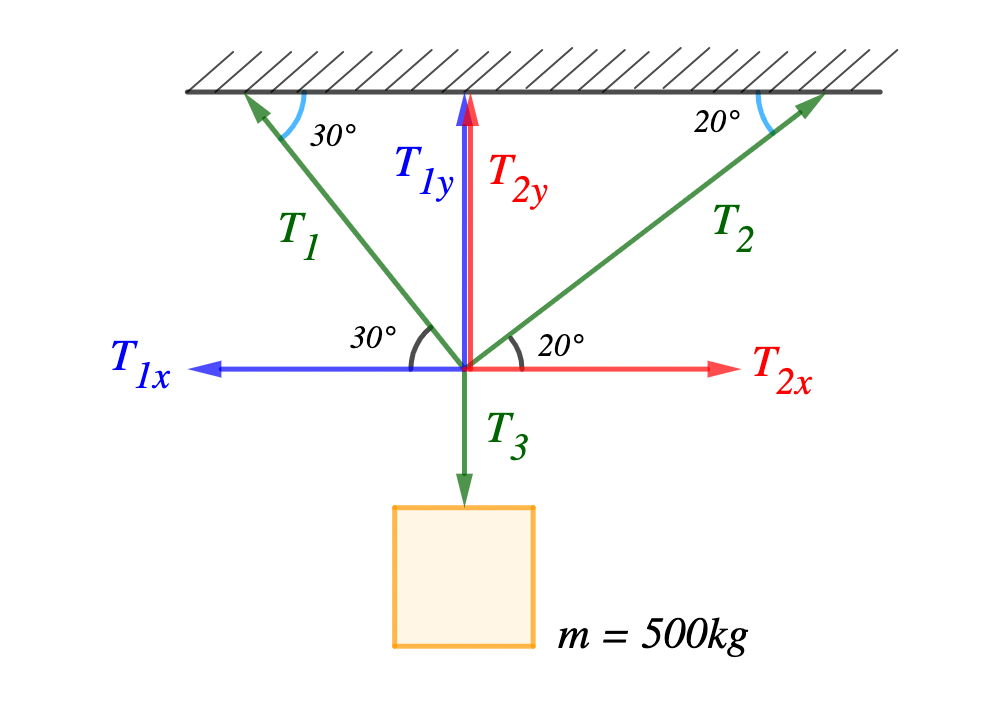
The horizontal component T_1x = T₁ cos 30º (Note: this is moving in the negative direction)