Time of Flight

If an object is projected with a velocity, U, and at an angle of inclination θ, with the horizontal from which it was projected, the vertical component of the velocity U_y, is U sin θ, while the horizontal component U_x, is U cos θ.

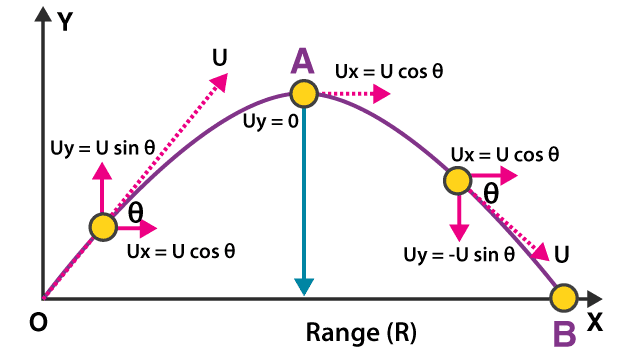
Initial horizontal component: U_x = U cos θ

Initial vertical component: U_y = U sin θ

Let us consider when the object is moving up in the y direction

When the object is moving up in the y direction, the acceleration = -g, because gravity is acting downwards.

The body moves along a parabolic path, reaches a maximum height and returns back down to the ground. When it reaches the ground again its vertical displacement is 0.

∴ as it hits the ground, y = 0

Using: \( \scriptsize s = ut \: + \: \normalsize \frac{1}{2} \scriptsize at^2 \)

s = y = 0

U = U_y = U sin θ

a = -g

T = t

We can use these values to calculate the time (T) it takes to finally hit the ground.

i.e. Time of flight, T = t

let’s substitute all the values into the equation: \( \scriptsize s = ut \: + \: \normalsize \frac{1}{2} \scriptsize at^2 \)

⇒ \( \scriptsize 0 = Usin \theta (T)\: – \: \normalsize \frac{1}{2} \scriptsize gT^2 \)

T = 0

OR

⇒ \( \scriptsize Usin \theta (T) = \normalsize \frac{1}{2} \scriptsize gT^2 \)

⇒ \( \scriptsize Usin \theta = \normalsize \frac{gT^2}{2T}\)

⇒ \( \scriptsize Usin \theta = \normalsize \frac{g\not{T}^2}{2\not{T}}\)

⇒ \( \scriptsize Usin \theta = \normalsize \frac{gT}{2}\)

⇒ \( \frac{gT}{2} = \scriptsize Usin \theta \)

⇒ \( \scriptsize T = \normalsize \frac{2Usin \theta}{g} \)

Alternative Method:

A second method is to consider the vertical velocity at the maximum height.

At the maximum height, the final vertical velocity of the projectile is 0, v = 0

using: v = U – gt

0 = U sin θ – gt