Topic Content:
- Components of a Vector
A vector, F, generally has two components, namely the vertical component of a vector Fy, and the horizontal component of a vector, Fx.
F = (Fx, Fy)
The component of a vector is the effective value of the vector in a particular direction.
The horizontal component of a vector F is the effective value of the vector in the horizontal direction (Fx)
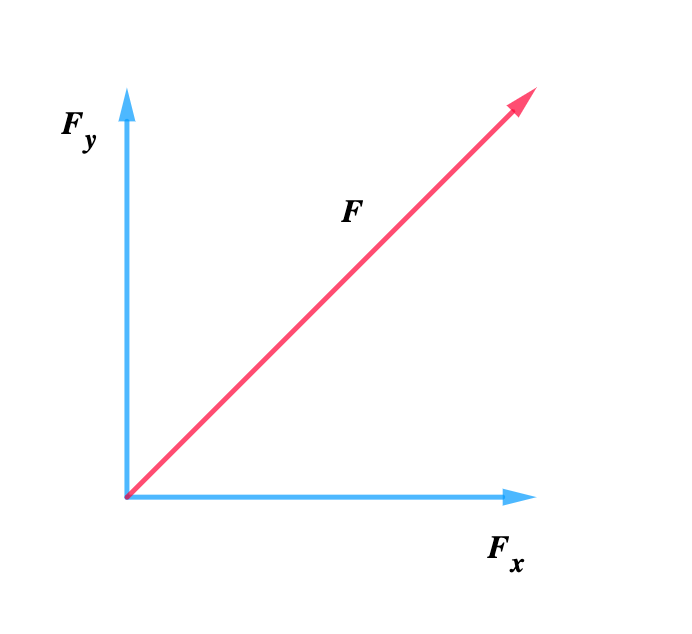
Use SOH CAH TOA to calculate the horizontal component Fx
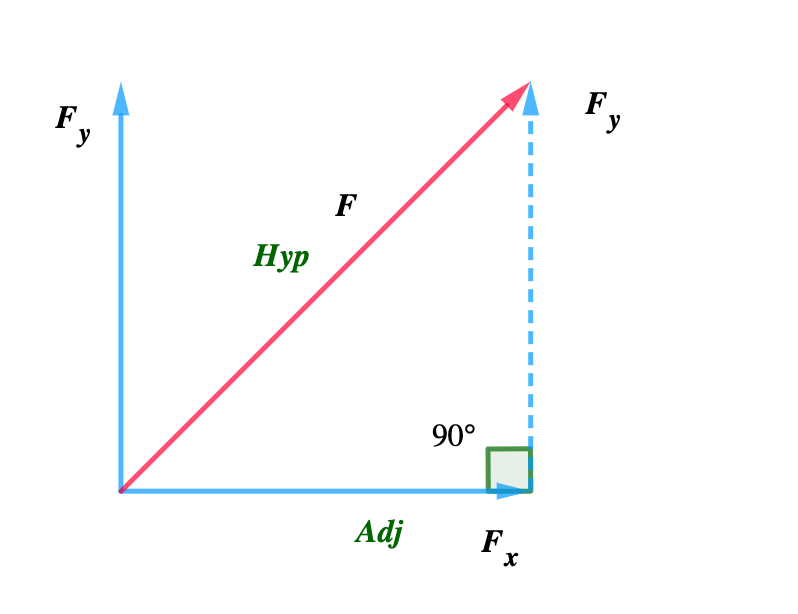
Fx = Adjacent, F = Hypotenuse, Therefore, we use CAH
Cos θ = \( \frac{Adj}{Hyp} \)
Cos θ = \( \frac{F_x}{F} \)
Fx = F Cos θ
You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!
Click on the button "Subscribe Now" below for Full Access!
Subscribe Now
Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!



Responses