Topic Content:
- Parallelogram Law of Vectors
- Derivation of the Law
- Direction of the Resultant Vector
This is used when two vectors are inclined at an angle to each other and it states that:
If two forces acting at a point are represented in magnitude and direction by the sides of the parallelogram drawn from that point, their resultant is represented in magnitude and direction by the diagonal of the parallelogram drawn from that point.
Derivation of the Law:
Let θ be the angle between B and D and R be the resultant vector. Then, according to parallelogram law of vector addition, diagonal OE represents the resultant of B and D.
So, we have
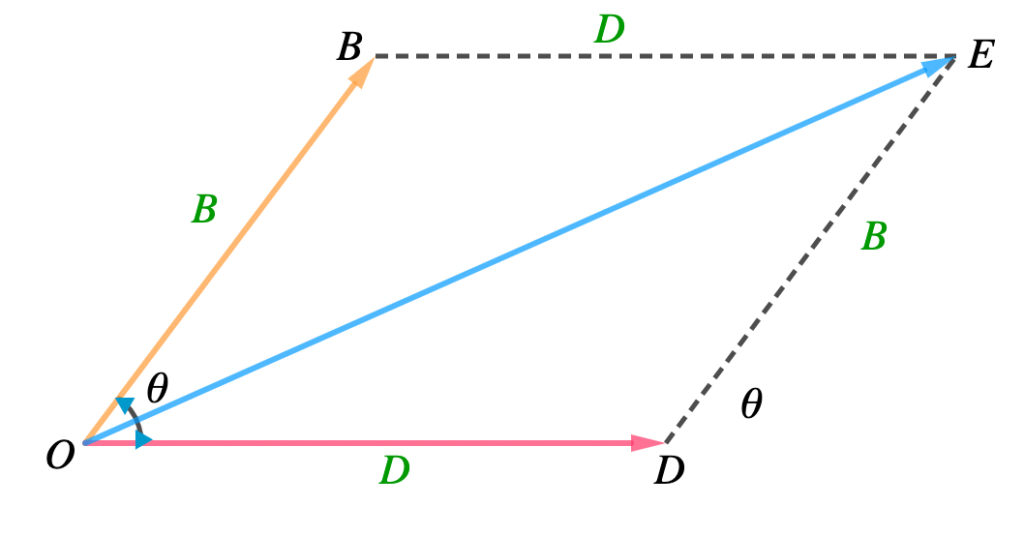
R = B + D
Now, expand O to F and draw EF perpendicular to OF.
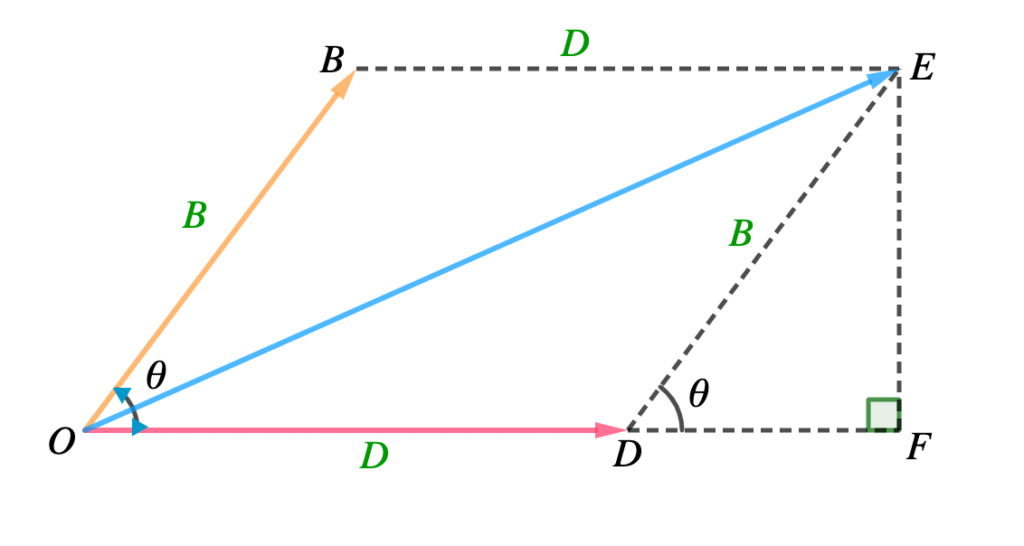
From ΔOFE,
OE2 = OF2 + EF2
But OF = OD + DF
∴ OE2 = (OD + DF)2 + EF2 ……..(i)
In ΔDEF,
You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!
Click on the button "Subscribe Now" below for Full Access!
Subscribe Now
Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!



How did we get 2DB cosO
(D + Bcosθ)^2
(D + Bcosθ)(D + Bcosθ)
open the brackets
D^2 + DBcosθ + DBcosθ + B^2cos^2θ
D^2 + 2DBcosθ + B^2cos^2θ
Splendid