Topic Content:
- Horizontal Oscillations of a Spring-Mass System
Consider a system containing a spring with a block of mass m attached to it on a smooth horizontal surface (frictionless surface) as shown below. The spring constant = k.
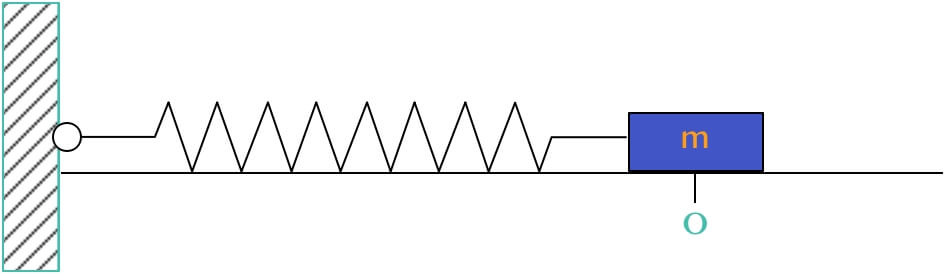
At this point, the block is at its central or equilibrium position, O.
If the mass is pulled towards the right, through a small displacement x from its equilibrium position, and then released, it will oscillate back and forth its equilibrium position, O.
You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!
Click on the button "Subscribe Now" below for Full Access!
Subscribe Now
Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!



Thank you ❣️