For a Simple Pendulum

Below we show that the motion of the bob of a simple pendulum is simple harmonic.

If a bob of mass, m, of a simple pendulum, is slightly displaced through a small angle and allowed to oscillate about O.

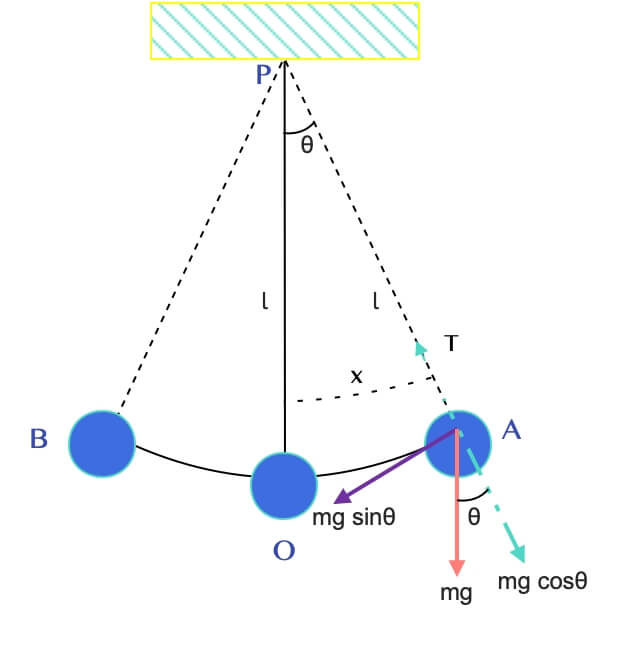
Suppose it is at A, at any instance in time during oscillations and θ is the angle POA, subtended by the string with the vertical.

mg is the force acting on the bob at point A in a vertically downward direction.

At A, the bob is at its extreme position. its velocity is zero, and its component mg cos θ is balanced by the tension in the string which is clear from Fig. 2 below.

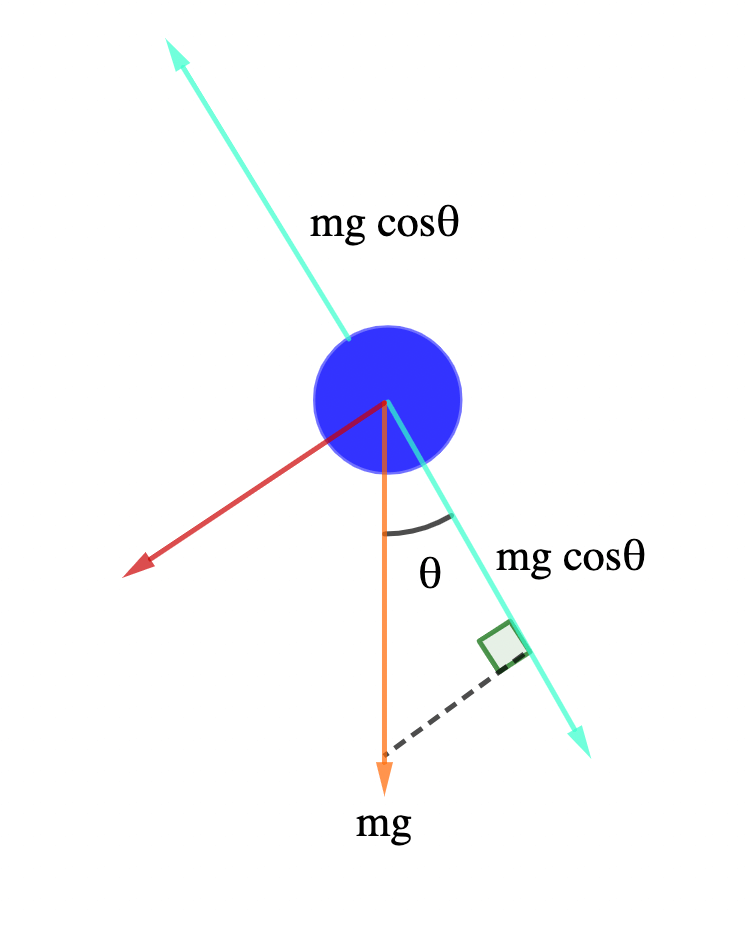
Hence the equation becomes: T − mgcosθ = 0

The force that tends to move it towards the centre O, in the direction opposite to increasing θ = -mg sinθ