Calculating Distance Along Parallels of Latitude

Considering right angle triangle LMO

Cos θ = \( \frac {r}{R} \)

i.e. r = R Cos θ

---

Example 1:

Find the distance between two points A(50^oN, 94^oW) and B(50^oN, 86^oE):

(i) Along the parallel of Latitude
(ii) Along a great circle

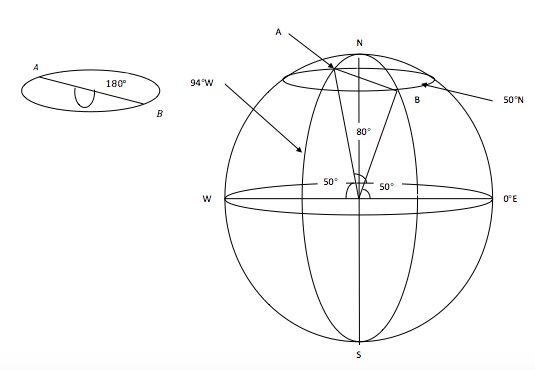
Solution:

(i) Angular difference = 94^o + 86^o = 180^o

i.e \( \scriptsize \bar{AB} = \normalsize \frac{180}{360}\scriptsize \; \times \; \scriptsize 2 \; \times \; \normalsize \frac{22}{7} \scriptsize \; \times \; 6400 \; \times \; cos50\)

= \( \frac{1}{2} \; \times \; \frac{44}{7} \scriptsize \; \times \; 6400 \; \times \; 0.6428\)

i.e \( \scriptsize \bar{AB} = 12,929.213 \)

i.e \( \scriptsize \bar{AB} = 13,000km \;(nearest\;kilometre) \)

(ii) Angular difference = 180^o – (50 + 50)^o

= 180^o – 100^o

= 80^o

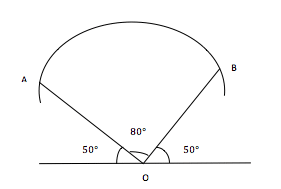
i.e \( \scriptsize \bar{AB} = \normalsize \frac{80}{360}\scriptsize \; \times \; \scriptsize 2 \; \times \; \normalsize \frac{22}{7} \scriptsize \; \times \; 6400 \)

= 8,939.6

i.e. \( \scriptsize \bar{AB} \) = 8,940Km (nearest Kilometre).

(Recall that it is clear that distance along a great circle is shorter i.e. 8,940Km < 13,000Km.

Example 2

Two points A and B are 800Km apart on the same Latitude with 20^o angular difference of longitude. Calculate:

(i) The Latitude
(ii) The speed of an aeroplane that travelled from A to B in 2hours
(iii) The speed of the point B due to the rotation of the earth. (Take \(\scriptsize \pi = \normalsize \frac{22}{7}\) and R = 6,400Km.)

Solution:

\( \scriptsize \bar{AB} = \normalsize \frac{20}{360} \scriptsize\; \times \; \scriptsize 2 \; \times \; \normalsize \frac{22}{7} \scriptsize \; \times \; 6400 \; \times \; cos θ\)

\( \scriptsize \bar{AB} = \normalsize \frac{1}{18}\scriptsize \; \times \; \normalsize \frac{44}{7} \scriptsize \; \times \; 6400 \; \times \; cos θ\)

\( \scriptsize 800 = \normalsize \frac{1}{18} \scriptsize \; \times \; \normalsize \frac{44}{7} \scriptsize \; \times \; 6400 \; \times \; cos θ\)

cos θ = \( \frac{18 \; \times \; 800 \; \times \; 7}{44 \; \times \; 6400} \)

θ = cos^-1(0.3580)        

θ = 69°

Let θ Latitude = θ° N       

∴   θ = 69° N

(ii) Speed = \( \frac{Distance}{time} \)

Time = 2hours, Distance = 800

i.e.     Speed(s) = \( \frac{800}{2} \)

Therefore, Speed = 400Km/h

(iii) Circumference of Latitude 69^o = 2 πr

Where r= RCos θ

i.e. Distance = \( \scriptsize 2 \; \times \; \normalsize \frac{22}{7} \scriptsize \; \times \; 6400 \; \times \; cos 69\) 

= 14,417Km

Therefore, Speed = \( \frac{Distance}{time} = \frac{14,417}{2} \)

= 7,208 Km/h.

Example 3

A plane leaves an airport X, 20.6^oE and 36.8^oN and flies due South along the same longitude for 8hours at the rate of 1000Km/h to another airport Y, 20.6^oE, and θ°. The plane then flies west to another airport Z for 8hours at the same speed.

Calculate, to the nearest degree:

(i) The value of
(ii) The longitude of Z

(Take π = \( \frac{22}{7} \) and R = 6,400Km.)

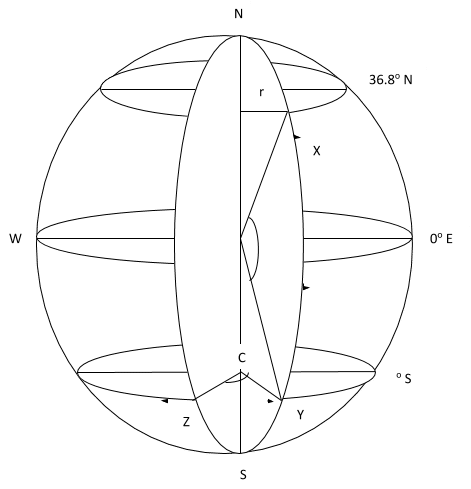
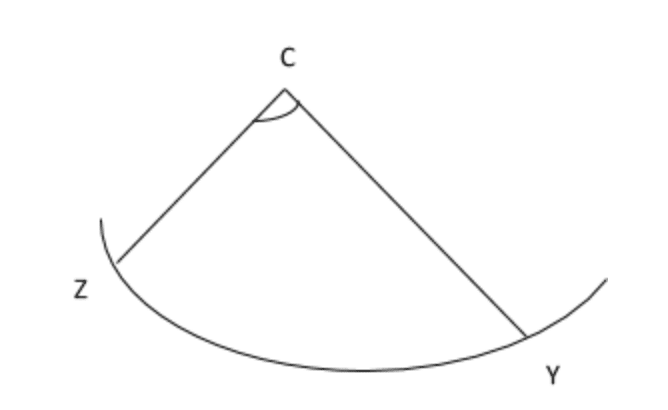
(i) Distance \( \scriptsize \bar{XY}\) = Speed  x  time

= 1000 x 8

= 8,000Km

i.e.  \( \scriptsize \bar{XY} = 8000 = \frac{θ}{360} \scriptsize \; \times \; \scriptsize 2 \; \times \; \normalsize \frac{22}{7} \scriptsize \; \times \; 6400 \)

i.e.      8000 = θ × 117.46032

i.e.     θ = 71.5909

θ = 72° nearest degree.

Angular difference = θ° S + 36.8°N

72 = θ + 36.8

θ = 35.2°

θ = 35°S nearest degrees.

(ii) \( \scriptsize \bar{ZY}\) = Speed  x  time

\( \scriptsize \bar{ZY}\) = 1000 x 8

i.e.  \( \scriptsize \bar{ZY}\) = 8,000Km

i.e.    \( \scriptsize \bar{ZY} = 8000 = \frac{θ}{360} \scriptsize \; \times \; \scriptsize 2 \; \times \; \normalsize \frac{22}{7} \scriptsize \; \times \; 6400 \; \times \; cos 35.2 \)

i.e.      8000 = θ × 91.312699

i.e.  θ = 87.6110335

i.e. Angular difference = 20.6^oE + θ°W

i.e. 87.611 = 20.6 + θ°W

i.e. θ°W = 67.011°W

Example 4:

A and B are two points on latitude 55^oS and their longitudes 23^oW and 33^oE respectively. Calculate the distance between A and B along:

(i) A great circle
(ii) The parallel of Latitude

(Take π = \( \frac{22}{7} \) and R = 6,400Km.)

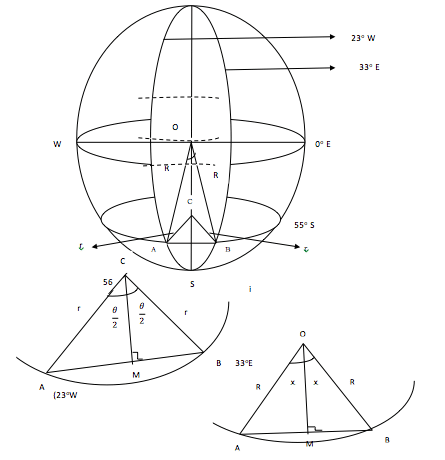
:- \( \scriptsize \bar{AM} = r sin \normalsize \frac {θ}{2}\)   

\(\scriptsize \bar{AM} = Rcos(Latitude) sin \normalsize \frac{\theta}{2} \) ………….….(a) 

\( \scriptsize \bar{AM} = R \)

i.e.   \( \scriptsize \bar{AM} = R sin x\)         ………………… (b) 

Equate equation (a) and (b)

R cos (latitude) \( \scriptsize sin \normalsize \frac {θ}{2}\scriptsize = R sin x \)

Therefore \( \scriptsize sin x = cos \; (latitude) \; sin \normalsize \frac {θ}{2} \)

i.e.    sin x   = Cos 55 Sin 28

i.e. x = sin ^-1 (0.5736×0.4695)  

= sin ^-1 (0.2693 )   

x = 15.6219

2x = 31.24° =31°

Therefore, \( \scriptsize \bar{AB} \) along a great circle = \( \frac{2x}{360} \; \times \; \scriptsize 2 \pi r \)

i.e \( \scriptsize \bar{AB}= \normalsize \frac{31.24}{360}\scriptsize \; \times \; \scriptsize 2 \; \times \; \normalsize \frac{22}{7} \scriptsize \; \times \; 6400 \)

i.e \( \scriptsize \bar{AB} \) = 3,491.38

i.e \( \scriptsize \bar{AB} \) = 3,491 km

(b) \( \scriptsize \bar{AB} \) along parallel of Latitude = \( \frac{θ}{360}\scriptsize \; \times \; \scriptsize 2 \pi R cos \; (latitude) \)

 i.e \( \scriptsize \bar{AB} =\normalsize \frac{56}{360}\scriptsize \; \times \; \scriptsize 2 \; \times \; \normalsize \frac{22}{7} \scriptsize \; \times \; 6400 \; \times \; cos 55 \)

= 3,589.31

i.e. \( \scriptsize \bar{AB} \) = 3,589Km.

Example 5

The position of P is (60^oS, 60^oW) and that of Q is (60^oS, 32^oE). Calculate the distance between P and Q along:

(i) The parallel of Latitude
(ii) A great circle

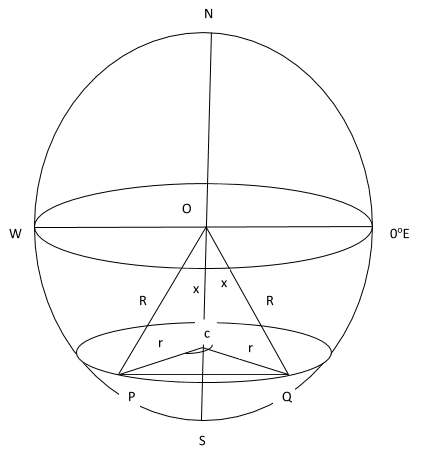
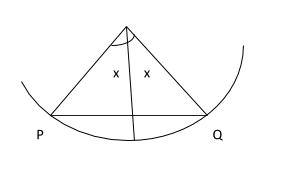
(i) \( \scriptsize \bar{PQ} = \normalsize \frac{θ}{360}\scriptsize \; \times \; \scriptsize 2 \pi R cos \; (latitude) \)

 i.e \( \scriptsize \bar{PQ} = \normalsize \frac{θ}{360} \scriptsize \; \times \; 2 \; \times \; \normalsize \frac{22}{7} \scriptsize \; \times \; 6400 \; \times \; cos 60 \)

\( \scriptsize \bar{PQ} \) = 5,140.3174603

\( \scriptsize \bar{PQ} \) = 5,140Km

(ii)Sin x = Cos 60 Sin46

= 0.5000 x 0.7193

Sin x = 0.3600

x = Sin^-1(0.3600)

x = 21.1^o

2x = 42.2^o

2x = 42^o

\( \scriptsize \bar{PQ} = \normalsize \frac{2x}{360}\scriptsize \; \times \; \scriptsize 2 \pi R \)

i.e \( \scriptsize \bar{PQ}= \normalsize \frac{42}{360}\scriptsize \; \times \; \scriptsize 2 \; \times \; \normalsize \frac{22}{7} \scriptsize \; \times \; 6400 \)

= 4,693.333

PQ = 4,693Km.