Use of Surds in Trigonometric Ratios

Recall the following trigonometric ratios of special angles 

Angle 45°	Angle 60°	Angle 30°
Sin 45° = \( \frac{1}{\sqrt{2}} \)	Sin 60° = \( \frac{\sqrt{3}}{2}\)	Sin 30° = \( \frac{1}{2} \)
Cos 45° = \( \frac{1}{\sqrt{2}} \)	Cos 60° = \( \frac{1}{2} \)	Cos 30° = \( \frac{\sqrt{3}}{2}\)
Tan 45° = 1	Tan 60° = \( \scriptsize \sqrt{3} \)	Tan 30° = \( \frac{1}{\sqrt{3}} \)

Example 1:

The diagonal of a rectangle is 4cm long and makes an angle of 60° with one side. What is the length, in cm, of the longest side of the rectangle?

Solution:

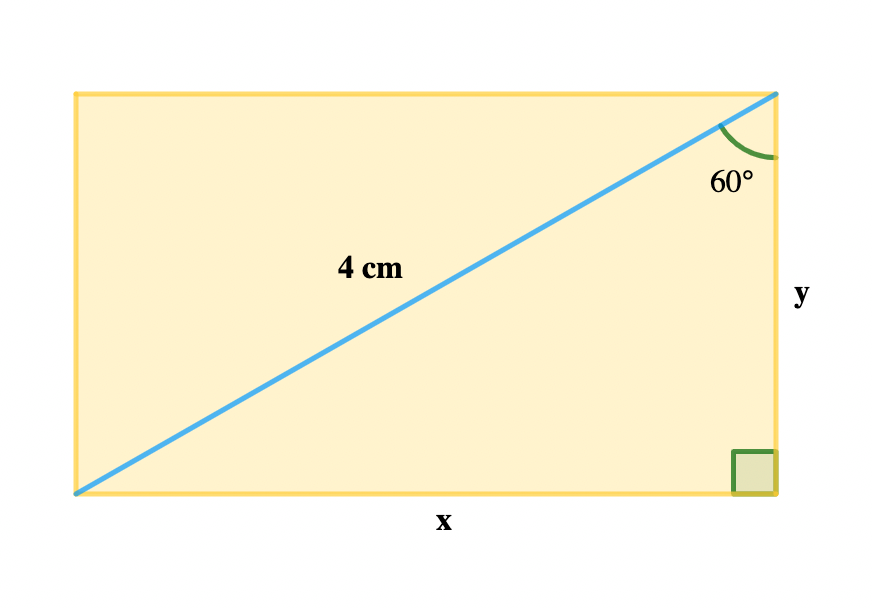
Sin 60° = \(\frac {opp}{hyp} = \frac{x}{4}\)

= \(\frac {\sqrt{3}}{2} = \frac{x}{4}\)

\( \scriptsize 2x = 4 \sqrt {3}\)

\( \therefore \scriptsize x = \normalsize \frac{4 \sqrt {3}}{2} \\ \scriptsize = 2 \sqrt {3}\)

Example 2:

From the top of a vertical mast 150m high, two huts are on the same ground level are observed, one due east and the other due west of the mast. Their angles of depression are 60° and 45° respectively. Find the distance between the huts.

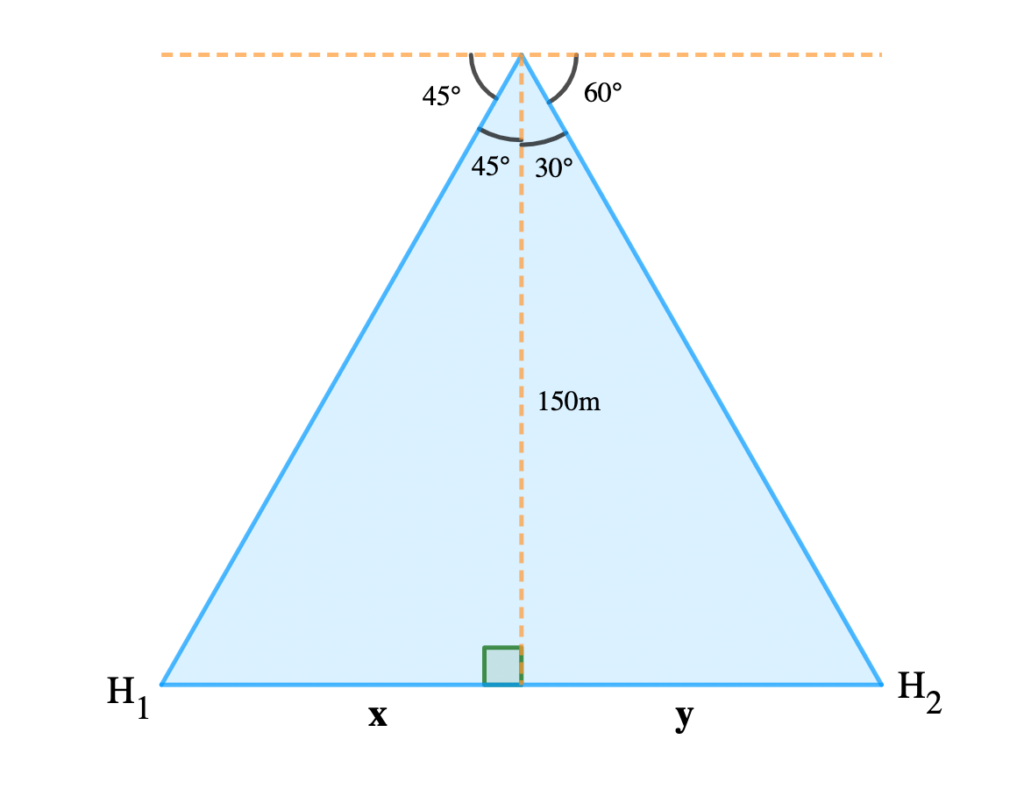
Distance between the huts =  |H₁H₂| = x + y

Tan 45° = \( \frac{x}{150} \)

x = 150 × tan45°

tan 45° = 1

∴ x = 150 × tan45°

x = 150m

tan 30° = \( \frac{x}{150} \)

y = 150 × Tan 30°

y = \( \scriptsize 150 \: \times \: \normalsize \frac{1}{\sqrt{3}} \)

= \( \frac {150 }{\sqrt{3}} \: \times \: \frac{\sqrt{3}}{\sqrt{3}} \)

= \( \frac {150 \sqrt{3} }{3} \scriptsize = 50 \sqrt{3}\)

|H₁H₂| = \( \scriptsize 150\: + \: 50 \sqrt{3}\)

= \( \scriptsize 50 \left (3 + \sqrt{3}\right) m\)