Tangent & Normal

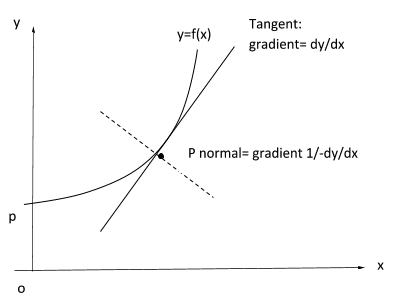
For a curve given by y = f(x), \( \frac{dy}{dx} \) is the gradient function. If given the coordinates of a point as on the curve, The value of \( \frac{dy}{dx} \) and the equation of the tangent at the point can be found.

Note: if two lines with gradients m₁, m₂ are perpendicular, then m₁, m₂ = -1

Hence the gradient of the line perpendicular to the tangent, the normal to the curve is \( \scriptsize m_2 = \normalsize \frac{-1}{m} \)

m₂ = \( \frac {-1}{\frac{dy}{dx}} \)

Examples:

1. Find the equation of the tangent and normal to the curve y = (1 – x)(2 + x), at the point where x = 2.

Solution:

y = (1 – x)(2 + x)

y = 2 – x – x²

\( \frac{dy}{dx} \) = -1 -2x

x = 2

y = 2 – 2 – (2²)

y = -4

Gradient of the tangent at the point (2, -4)

\( \frac {dy}{dx} \scriptsize = -1 \; – \; 2x \\ \scriptsize = \; -1 \; – \; 2(2) \\ \scriptsize = 5 \)

y + 4 = -5(x – 2)

So its equation is y + 5x = 6

Gradient of the normal at the point = \( \frac{1}{5} \) and its equation is

y + 4 = \( \frac {1}{5} \scriptsize(x \; – \; 2) \\ \scriptsize 5y = x \; – \; 22\)