Applications of Integration

Areas under curves

Consider the area A of the figure bounded by the curve y = f(x) , the x – axis and the y vertical lines through x = a and x = b and (where b > a)

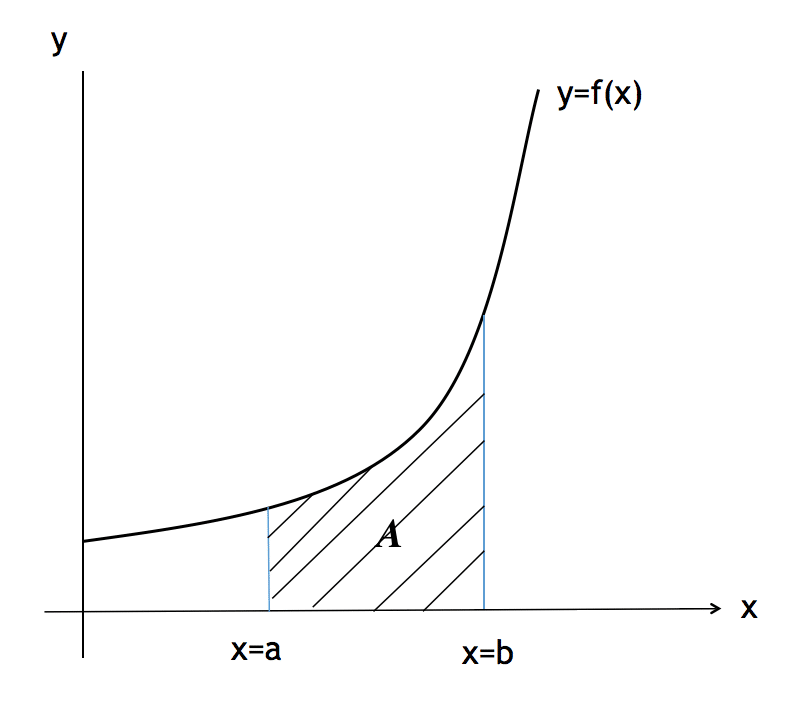
If x = b then \(\scriptsize A_b = \int\limits_{x=b} y dx \)(the value of the integral and hence the area up to b )

and if x = a then\(\scriptsize A_a = \int\limits_{x=a} y dx \) (the value of the integral and hence the area up to a ).

Since b > a, the difference in these two areas \(\scriptsize ( A_b – A_a) \) gives the required area A.

A = \(\scriptsize \int\limits_{x=b} y dx\; – \; \int\limits_{x=a} y dx \)

, this is called definite integral of f(x) with respect to x, between the limits a (the lower limit) and b (the upper limit). It is a function of a and b.

The arbitraryAn arbitrary rule, action or decision often seems unfair because it is not based on any principle, plan or system. An arbitrary legal judgment is a decision made at the discretion... More constants disappear in subtraction.

Example: 

Find the area bounded by the curve y = 3x²+ 6x + 8 , the x-axis and ordinate x = 1 and x = 3 .

Solution: 

A = \( \scriptsize \int_{1}^{3} ydx = \int_{1}^{3} \left ( 3x^2 + 6x + 8 \right) dx \)

A = \( \left[ \frac{3x^3}{3} + \frac{6x^2}{2} + \scriptsize 8x \right]_1^3\)

= \( \left[\scriptsize x^3 + 3x^2 + 8x \right]_1^3\)

A = \( \left[\scriptsize (3)^3 + 3(3)^2 + 8(3) \right] \; – \; \left[\scriptsize (1)^3 + 3(1)^2 + 8(1) \right]\)

A = 78 – 12

A = 66 units²

Volumes of Revolution

V = \( \scriptsize \int_{a}^{b}\pi^2 y^2 dx\)

Where y = f(x)  and V is the volume of solid generated when the curve y = f(x) is rotated completely around the x axis between limits x = a  and x = b .

Similarly, if a portion of the curve  y = f(x) between the limits y = a   and y = b, is rotated completely around the  axis, the volume of the solid generated will be given by

V = \( \scriptsize \int_{a}^{b}\pi^2 x^2 dy\)

Example: 

1. The part of the curve y = x^3  from (1, 1)  to (2, 8)  is rotated completely around the y axis. Find the volume of the solid generated.

Solution:

We shall express the integrand in terms of y, as we are integrating with respect to y.

V = \( \scriptsize \int_{a}^{b}\pi^2 x^2 dy\)

y = x³

∴ x = \( \scriptsize \sqrt [3]{y} \)

x = \( \scriptsize y ^{\frac{1}{3}} \)

Then x² = \( \scriptsize \left( y ^{\frac{1}{3}} \right)^2 \\ \scriptsize = y ^{\frac{2}{3}} \)

Note, the limits of y corresponding to x = 1 and x = 2 are y = 1  and y = 8.  

V = \( \scriptsize \int_{1}^{8}\pi y ^{\frac{2}{3}} dy\)

= \( \scriptsize \pi \left [ \normalsize \frac{y ^{\frac{2}{3}\; +\; 1}}{\frac{2}{3} \; + \; 1} \right]_1^8 \)

= \( \scriptsize \pi \left [\normalsize \frac{3}{5} \scriptsize y ^{\frac{5}{3}} \right]_1^8 \)

V = \( \scriptsize \pi \left [ \frac{3}{5} \scriptsize (8) ^{\frac{5}{3}} \right] \; – \; \scriptsize \pi \left [ \frac{3}{5} \scriptsize (1) ^{\frac{5}{3}} \right] \)

V = \( \scriptsize \pi \left [ \frac{3}{5} \scriptsize (\sqrt [3]{8}^5) \right] \; – \; \scriptsize \pi \left [ \frac{3}{5} \scriptsize (1) ^{\frac{5}{3}} \right] \)

V = \( \scriptsize \pi \left [ \frac{3}{5} \; \times \; \scriptsize (2^5) \right] \; – \; \scriptsize \pi \left [ \frac{3}{5} \; \times \; 1 \right] \)

V = \( \scriptsize \pi \left [ \frac{3}{5} \; \times \; \scriptsize 32 \right] \; – \; \scriptsize \pi \left [ \frac{3}{5} \; \times \; 1 \right] \)

V = \( \frac {96\pi}{5} \; – \; \frac {3\pi}{5} \)

V = \( \frac {93}{5} \scriptsize \pi\)

Example

2. Find the volume generated by rotating the curve y = x + 1 from x = 1  to  x = 2 completely round the x axis.

Solution:

V = \( \scriptsize \int_{a}^{b}\pi^2 y^2 dx\)

a = 1, b = 2, y = x + 1

∴y² = (x + 1)^²

V = \( \scriptsize \pi \left [\normalsize\frac{(x \; + \; 3)^3}{3} \right]_1^2 \)

∴V = \( \frac {\pi}{3}\scriptsize \left [ ( x \; + \; 1)^3 \right]_1^2 \)

V = \( \frac {\pi}{3} \scriptsize (3)^3 \; – \; \frac {\pi}{3} \scriptsize (2)^3 \\ = \frac{27 \pi}{3} \; – \; \frac{8 \pi}{3} \\ = \frac{27 \pi \; – \; 8 \pi}{3} \)

V = \( \frac{19 \pi}{3} \scriptsize unit \; cube \)