A French scientist, Charles Coulomb investigated the nature and magnitude of force between charges and came out with his findings known as Coulomb’s law.
Coulomb’s law states that the force [F] of attraction or repulsion between two charges is directly proportional to the product of their charges Q1 and Q2 and inversely proportional to square of the distance between them.
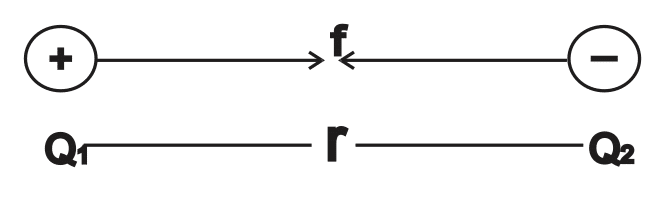
F = \( \scriptsize k \normalsize \frac{Q_1 Q_2}{r^2}\)
Where k = constant of proportionality
k = \( \frac{1}{4 \pi \varepsilon_0} \scriptsize = 9.0 \: \times \: 10^9 Nm^2 C^{-2}\)
\( \scriptsize \varepsilon_0 \)= permittivity of air or free space = 8.85 x 10-12 Fm-1
Materials with high permittivity allow current to pass through them
F = \( \frac{1}{4 \pi \varepsilon_0} \frac{Q_1 Q_2}{r^2} \)
Example
Calculate the force of attraction between two protons of charge 1.6 x 10 -19c each if the distance between them is 5.3 x 10 -11m.
(Take \( \frac{1}{4 \pi \varepsilon_0} \) = 9 x 109 Nm2 C-2 )
Solution
F = \( \frac{1}{4 \pi \varepsilon_0} \frac{Q_1 Q_2}{r^2} \)
Q1 = Q2 = Q
F = \( \frac{1}{4 \pi \varepsilon_0} \frac{Q . Q}{r^2} \)
= \( \frac{1}{4 \pi \varepsilon_0} \frac{Q^2}{r^2} \)
F = \( \scriptsize 9 \times 10^9 \normalsize \frac {\left (1.6 \times 10^{-19} \right)^2}{\left (5.3 \times 10^{-11} \right)^2}\)
= 8.2 x 10 -16 N



Responses