The a.c generator consists of:
- an armature- a rectangular coil consisting of a large number of an insulated wire wound on a laminated soft iron core
- a magnetic field- created by the curved poles of a horse shoe magnet or an electromagnet
- two copper slip rings R1, R2– to which ends of rectangular coils are connected and which rotate with the armature
- two stationary carbon brushes : which are made to press lightly against the slip rings
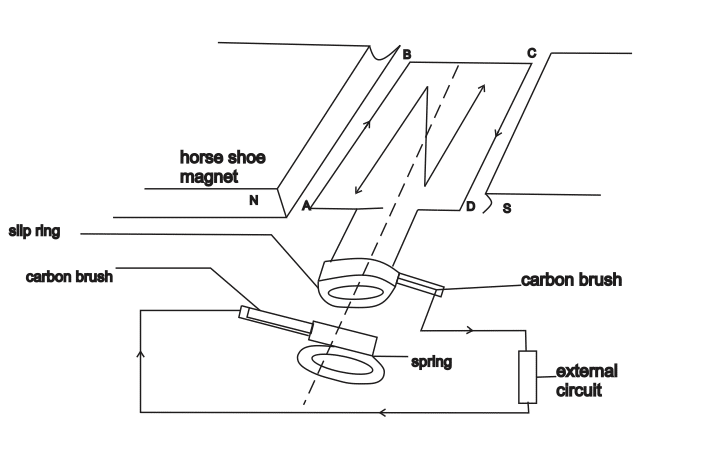
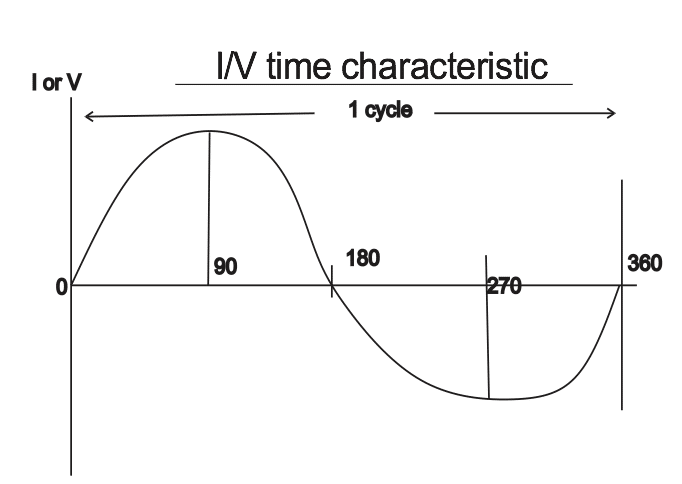
An alternating voltage whose waveform is obtained above at the terminals by means of carbon brushes and slip rings
If the coil of area A rotates in magnetic field of strength B. Let the normal to the coil make an angle θ with the field as shown,
Flux θ through the coil is given by φ = ABCosθ ________(1)
If there are N number of turns in the coil, then, φ = NABcosθ _________(2)
If the coil turns with a steady angular velocity ω is given by
ω = \( \frac{dθ}{dt} \) _________(3)
the induced e.m.f is given by
E = \( \frac{- dθ}{dt} \) _________(4)
The above equation follows from Faraday’s and Lenz’s laws
E = \( \frac{- dθ}{dt} = \frac{- d}{dt} \scriptsize (NABcosθ) \)
E = \( \scriptsize – NAB \normalsize \frac{ d}{dt} \scriptsize (cosθ) \)
E = \( \scriptsize NAB sinθ \normalsize \frac{ dθ}{dt} \) _______(5)
From equation (3) ω = \( \frac{dθ}{dt} \)
∴ E = NABω sinθ __________(6), if θ = 90 , then equation 6 becomes
E = NABω = EO ___________(7)
where EO is the maximum induced e.m.f which occurs when the coil is parallel to the field direction.
E = EOsinθ, but ω = \( \frac{dθ}{dt} \), θ = ωt
E = EOsinω t ______________(8)
Alternating current a.c is a current which changes continually in direction while passing through a conductor
Measurement of A.C
An a.c can be measured by:
Hot-wire ammeter- using the heating effect of current
Moving iron ammeter- using the magnetic field of current
Moving coil galvanometer to which a rectifier is attached to convert a.c to d.c



Responses