Half Life

Half-life of a radioactive element is the time taken for half of the atoms initially present in the element to decay

Stable elements have long half-life while elements with short half -life are unstable

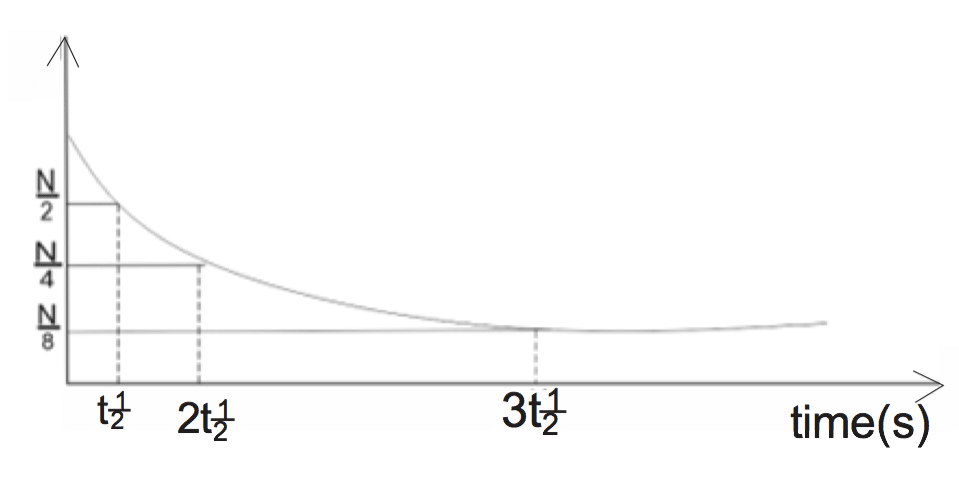
If N is the number of atoms present initially, half of N = (\( \frac{N}{2} \)) will decay at T\( \frac{1}{2} \) if the half-life of the atom is 10 seconds, in another 10 seconds, it will decay to (\( \frac{N}{4} \)), etc.The rate of decay of the radioactive element is directly proportional to the number of atoms of the material present. The unit of decay is Becquerel (B_q)

Rate of decay \( \scriptsize \propto \) number of atoms initially present

\( \frac{dn}{dt} \scriptsize \propto N \)

or

N = \( \scriptsize -\lambda \normalsize \frac{dn}{dt} \)

The constant λ is the disintegration or decay constant of the radioactive element 

Decay constant (λ) is the ratio of number of atoms disintegrating per second to the number of atoms in the source at that time.

Also,

N = \( \scriptsize N_0 e^{-\lambda t} \) __________(1)

N₀ – number of atoms present at time t = 0

N – number of atoms present at time t 

For half -life, let N= \( \frac{1}{2} \scriptsize N_0 \)No and substitute in equation 1

\( \frac {N_0}{2} \scriptsize = e^{-\lambda t} \)

\( \frac {1}{2} \scriptsize = e^{-\lambda t} \)

Taking natural logarithm of both sides,

\(\scriptsize \log e \frac {1}{2} \scriptsize = -\lambda t \)

Since \(\scriptsize \log e \normalsize \frac {1}{2} \) = log_e1 – log_e2 = 0 – log_e2

= – 0.693

∴ -0.693 = \(\scriptsize \lambda t_{\frac{1}{2}} \)

t = \(– \frac {0.693}{\lambda} \)

Example

The half-life of a radioactive element is 4 seconds. If there are 20,000 atoms initially present, calculate the

(i) decay constant of the element

(ii) the number of atoms remaining after 8 seconds

(iii) fraction of the atom that decayed after 8 seconds

Solution

\( t_{\frac{1}{2}}\; = \; – \frac {0.693}{\lambda}\)

\( \scriptsize \lambda \; = \; -\frac {0.693}{t_{\frac{1}{2}}}\)

=\( -\frac {0.693}{4}\)

= 0.173secs

(ii) At t₀ = 4

\( \frac {N}{2} = \frac {20000}{2}\)

= 10000 atoms

(ii) At t₀ = 8

\( \frac {N}{4} = \frac {20000}{4}\)

= 2500 atoms

The number of atoms that decayed is 20000 – 2500

=17500