Resistance | Capacitance | Inductance in an A.C Circuit

Resistance in an A.C Circuit

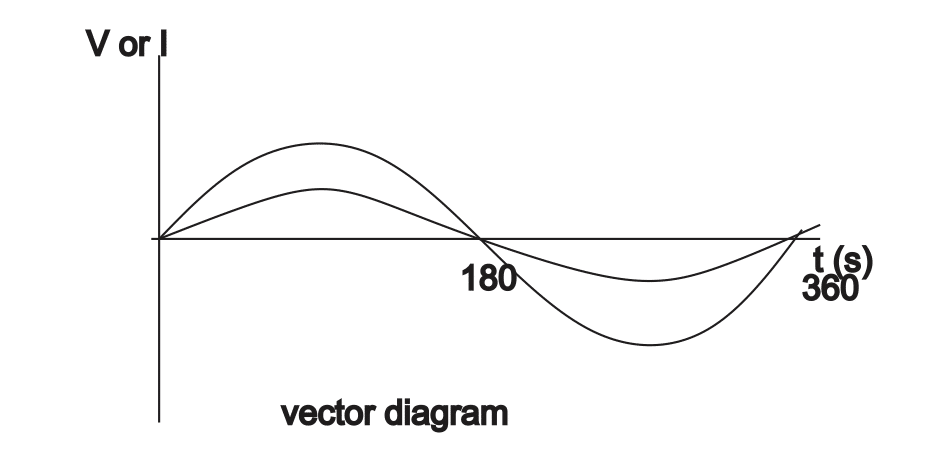
The a.c current and voltage flowing through a resistor are in phase, they attain a maximum and minimum values at the same time. The value of current is I = I₀Sinωt, the voltage, V = V₀Sinωt

from Ohm’s law, V = IR, I = \( \frac{V}{R} \)  

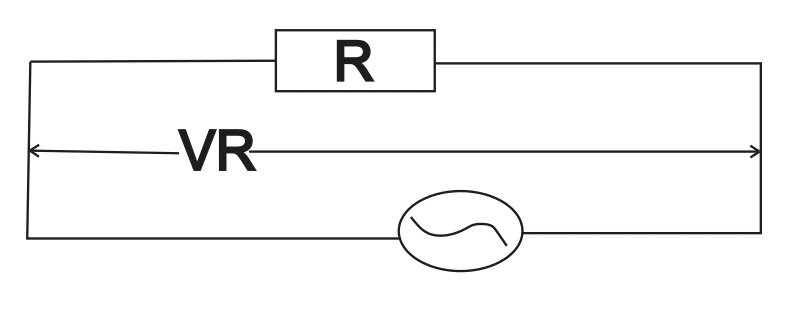
If V = V₀Sinωt.

R =\( \frac {V_o Sin \omega t}{I_o Sin \omega t}= \frac{Vrms}{Irms} \) 

R = \( \frac {V_o }{I_o }= \frac{Vrms}{Irms} \)

Irms =  \(\frac{Vrms}{R} \)

---

Capacitance in an A.C Circuit

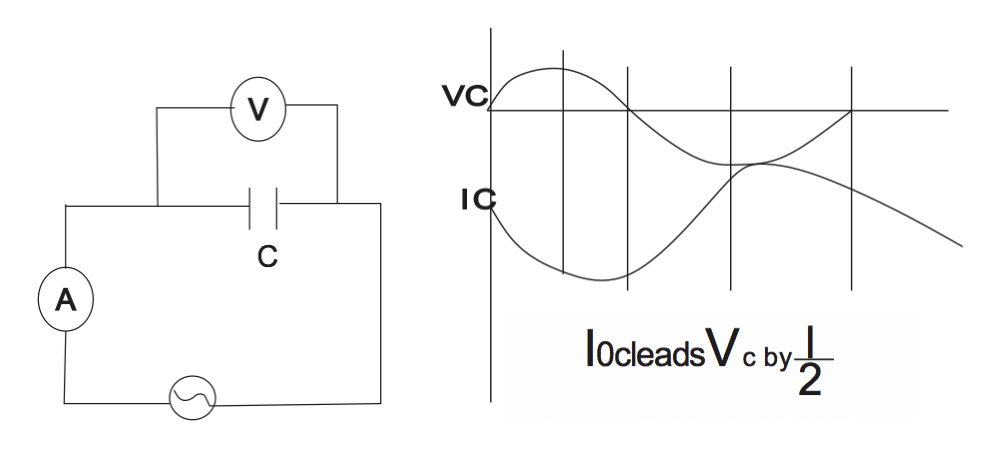
The voltage (V) and current (I) are out of phase, the current lead the voltage by \( \frac {pi}{2 }\)  or 90⁰ or voltage lags the current by \( \frac {pi}{2 }\)

If capacitor oppose flow of current, hence the opposition offered by a capacitor to flow of an a.c is known as capacitive reactance, Xc

Xc = \( \frac {1}{2 \pi f c} \ \frac{1}{\omega c}\) 

V = IXc

The unit of Xc is ohms.

Xc = capacitive reactance, c = capacitance of capacitor in Farad

f = frequency of the source in Hertz (Hz).

---

Inductance in A.C Current

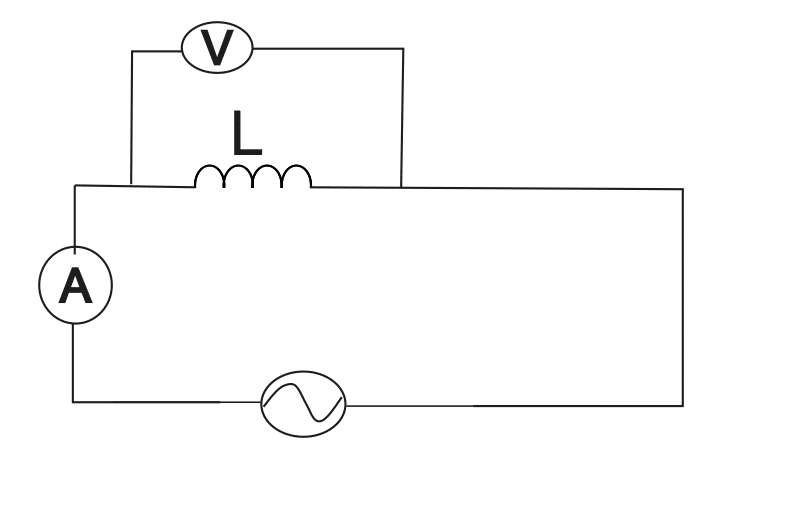
Inductive reactance is the opposition to the flow of an a.c current offered by an inductor.

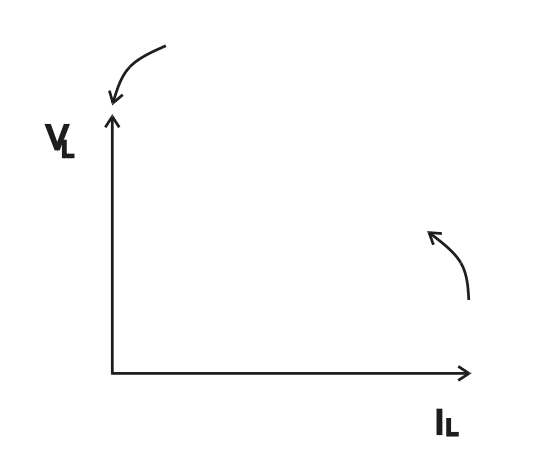
V_L leads I_L by \( \frac {\pi}{2 } \scriptsize \; or \; 90^{\circ}\)

X_L= if V = V_Osinωt, I = I_O \( \left( \scriptsize sin\omega t – \normalsize \frac {\pi}{2 } \right) \)

Since an inductor opposes the flow of current, the inductive reactance is

X_L, then V =IX_L

X_L= 2πfL = ωL

The unit of L is henry (H). The unit X_L is (Ω).

A reactance is the opposition to the flow of a.c offered by a capacitor or an inductor or both.

Examples

1. An inductor of 0.7H is connected to an A.C Source of 220V. Calculate 

(i) Inductive reactance

(ii) current flowing through the circuit

(iii) energyEnergy is the ability to do work. Energy exists in several forms such as heat, kinetic or mechanical energy, light, potential energy, and electrical energy. Units of Energy: The SI unit... More dissipated in the inductor (f =  \( \frac {100}{\pi} \) Hz)

Solution 

(i) X_L= 2πfL

= \(\scriptsize 2 \pi \; \times \; \normalsize \frac {100}{\pi} \; \times \; 0.7 \)

= 140Ω

(ii) V = I x L

I = \( \frac {V}{XL} = \frac {220}{140} \)

I = 1.57A

(iii) W = \( \frac {1}{2} \scriptsize LI^2 \)

=  \( \frac {1}{2} \scriptsize \times 0.7 \times 1.57^2 \) 

= 0.86J

2. A 2 F capacitor is connected directly across a 150Vrms, 60Hz a.c source. Find (i) r.m.s value of the current (ii) peak value of the current

Solution 

X_C = \( \frac {1}{2 \pi f c}  =\frac {1}{2 \pi \; \times \; 60 \; \times \; 2 \times 10^{-6}f c}  \)  

X_C = 1324.4Ω

V = I x C

I_rms= \( \frac {V_{rms}}{x_c}  = \frac {150}{1324.4} \)  

I_rms = 0.11A

I_rms =  \( \frac {I_0}{\sqrt{2}} \)

I_O = I_rms x √2

= 0.11 x 0.707

=0.160A