The Transformer
A transformer is an electric device for changing the size of an a.c voltage. It increases or decreases the e.m.f of an alternating circuit.
Structure
A transformer has two coils a primary coil and the secondary coil each wound on a laminated soft iron core magnetically linked to the two coils.
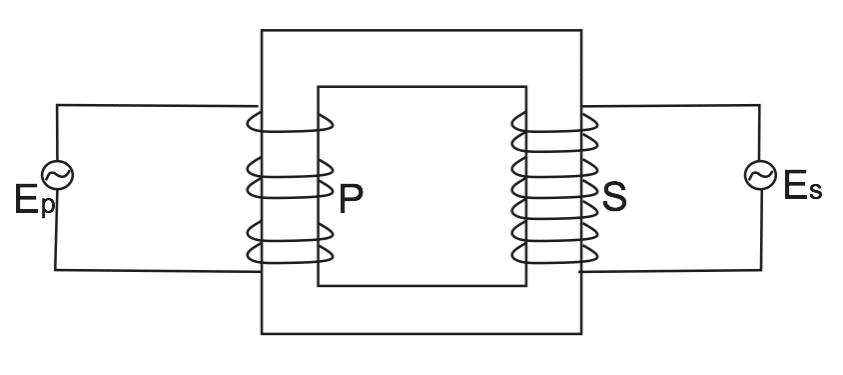
The soft iron core acts to increase and concentrate magnetic flux within the core. It is also laminated to reduce loss of energyEnergy is the ability to do work. Energy exists in several forms such as heat, kinetic or mechanical energy, light, potential energy, and electrical energy. Units of Energy: The SI unit... More in the form of heat due to eddy current induced in the core
The primary coil is connected to the a.c source to be step up or step down while the secondary coil is connected to the load
When an a.c or an e.m.f (EP) is applied at the terminal of primary coil (P), an alternating magnetic flux is produced in the iron core which links the secondary coil (S), an alternating e.m.f (Es) of the same frequency as that in EP is induced in the secondary coil by mutual inductance.
Mutual inductance is the ability of a coil to induce current or voltage in another coil by changing the current flowing through it.
The total flux linking the two coils is proportional to their number of turns, NP is the number of turns in the primary coil and NS number of turns in the secondary coil.
The induced e.m.f in the secondary coils (ES) depends on the e.m.f in the primary coil and on the ratio of the number of each turn in each coil
\( \frac{E_s}{E_p} = \frac{N_s}{N_p} \)For ideal transformer with 100 efficiency, power developed in the secondary coil is equal to the power developed in the primary coil. From conservation of energy,
\( \scriptsize E_s \; \times \; I_s \; =E_p \; \times \; I_p \)But \( \frac{E_s}{E_p} = \frac{N_s}{N_p} \)
∴ \( \frac{E_s}{E_p} = \frac{N_s}{N_p} = \frac{I_p}{I_s} \)
Examples
A transformer is required to give 120v from a 240v mains supply. If the primary has 5500 turns, how many turns has the secondary?
Solution
Es = 12OV, Ep = 24OV, Ns = 5500, Ns = ?
\( \frac{E_s}{E_p} = \frac{N_s}{N_p} = \frac{I_p}{I_s} \)Ns = \( \frac{E_s \times N_p}{E_p}\)
Ns = \( \frac{120 \times 5500}{240}\)
Ns = 2750 turns
Efficiency of a transformer is
E = \( \frac{output \; power }{input \; power}\scriptsize \; \times \; 100 \% \)
E = \( \frac{power \; in \; the \; secondary \; coil}{power \; in \; the \; primary \; coil}\scriptsize \; \times \;100 \% \)
= \( \frac{I_s V_s}{I_p V_p}\scriptsize \; \times \; 100 \% \)
\(\scriptsize I_s V_s = I_p V_p\) \(\)


Responses