Back to Course

WAEC: MATHEMATICS

0% Complete
0/0 Steps

Quizzes




  • Kofa Study
Quiz 14 of 16

2015 Mathematics WAEC Theory Past Questions

WAEC: MATHEMATICS 2015 Mathematics WAEC Theory Past Questions

Responses

Your email address will not be published. Required fields are marked *

Question 1a

(a) Without using Mathematical tables or calculators, simplify:

\( \scriptsize 3 \frac{4}{9} \: \div \: \left( 5 \frac{1}{3}   \: – \: 2 \frac{3}{4} \right) \: + \: 5 \frac{9}{10}  \)

Solution: Step 1:  Use BODMAS, the brackets should be solved first. Change the mixed numbers to improper fractions to make it easier.

\( \scriptsize 3 \frac{4}{9} \: \div \: \left(\normalsize \frac{16}{3}   \: – \:  \frac{11}{4} \right) \scriptsize \: + \: 5 \frac{9}{10}  \) \( \scriptsize 3 \frac{4}{9} \: \div \: \left(\normalsize \frac{64 \: – \: 33}{12}   \right) \scriptsize \: + \: 5 \frac{9}{10}  \) \( \scriptsize 3 \frac{4}{9} \: \div \: \left(\normalsize \frac{31}{12}   \right)\scriptsize  \: + \: 5 \frac{9}{10}  \)

Step 2: We take “D” – division next, change the mixed numbers to improper fractions

= \( \left( \frac{13}{9} \: \div \:  \frac{31}{12}   \right)   \: + \: \frac{59}{10}  \)

= \(  \left( \frac{13}{9} \: \times \:  \frac{12}{31}   \right)  \: + \: \frac{59}{10}  \)

= \(  \left( \frac{12}{9}   \right)   \: + \: \frac{59}{10}  \)

= \(  \frac{4}{3}     \: + \: \frac{59}{10}  \)

= \(  \frac{40 \: + \: 177}{30}     \)

= \(  \frac{217}{30}     \)

= \(  \scriptsize 7 \frac{7}{30}    \)

Question 1b

(b) A number is selected at random from each of the sets {2, 3, 4} and {1, 3, 5}. Find the probability that the sum of the two numbers is greater than 3 and less than 7.

Solution:

Step 1: Set out the table for the addition of the numbers as shown below

+

2

3

4

1

3

4

5

3

5

6

7

5

7

8

9

Step 2: Let E be the event that the sum is greater than 3 and less than 7

E = {4, 5, 5, 6}

Step 3: The sample space is 9

Probability(E) = \( \frac{4}{9} \)

Question 2a

(a) Solve the inequality

\( \scriptsize 4 \: + \: \normalsize \frac{3}{4} \scriptsize(x \: + \: 2) \leq \normalsize \frac{3}{8}  \scriptsize x \: + \: 1 \)

Solution: Step 1: Multiply through by 8

\( \scriptsize 4 \: \times \: 8 \: + \: \normalsize \frac{3}{4} \scriptsize(x \: + \: 2)  \: \times \: 8\leq \normalsize \frac{3}{8}  \scriptsize x \: \times \: 8 \: + \: 1 \: \times \: 8 \)

Step 2: Simplifying further we have

\( \scriptsize 32 \: + \: 6(x \: + \: 2) \leq 3x \: + \: 8 \) \( \scriptsize 32 \: + \: 6x \: + \: 12 \leq 3x \: + \: 8 \) \( \scriptsize  6x \: – \: 3x \: + \: 44 \leq  8 \) \( \scriptsize  3x \leq  8 \: – \: 44 \) \( \scriptsize  3x \leq \:  -36 \) \( \scriptsize  3x \leq \:  \normalsize \frac{-36}{3} \) \( \scriptsize  x \leq \:  -12 \)

Question 2b

(b) The diagram shows a rectangle PQRS from which a square of side x cm has been cut. If the area of the shaded portion is 484cm2, find the values of x.

Solution:

Step 1: Area of the shaded portion = Area of rectangle

PQRS – Area of the square

Step 2: Area of rectangle PQRS

= 20 x (20 + x)

= 20 (20 + x) cm2

Area of square = \( \scriptsize x \: \times \: x = x cm^2 \)

Area of the shaded portion = 20 (20 + x) – x2

Step 3: But the area of the shaded portion is given as 484cm2

484 = 20(20 + x) – x2

Step 4: Now solve the quadratic equation to determine the values of x

484 = 400 + 20x – x2

x2 – 20x + 84 = 0

x2 – 14x – 6x + 84 = 0

x(x – 14) – 6 (x – 14) = 0

(x – 14) (x – 6) = 0

  x = 14 or 6

Question 3a

The ratio of the interior angle to the exterior angle of a regular polygon is 5:2. Find the number of sides of the polygon.

Solution:

Step 1: Let x be the size of one exterior angle of the polygon, then we have the given ratio written as 

\( \frac{5}{2} \scriptsize x: x \)

Step 2: But \( \frac{5}{2} \scriptsize x \: + \:  x  = 180^o\)

[The sum of the interior and exterior angles of a polygon]

\( \frac{5}{2} \scriptsize x \: + \:  x  = 180^o\)

\( \frac{7}{2} \scriptsize x  = 180^o\)

7x = 3600

x = \( \frac{360}{7} \)

Step 3:  The number of sides of an n-sided polygon is given by

 n = \( \frac{360^o}{the \: size \: of \: its \: exterior \: angle} \)

 n = \( \frac{360^o}{1} \: \div \: \frac{360^o}{7} \)

 n = \( \frac{360^o}{1} \: \times \: \frac{7}{360^o} \)

 n = 7

The polygon has 7 sides.

Question 3b

The diagram shows a circle PQRS with centre O, <UQR = 680, <TPS = 740 and <QSR = 400 . Calculate the value of <PRS.

Solution

Step 1:

\( \scriptsize \hat{PSR} = 68^o \)

[Interior angle of a cyclic quadrilateral = opposite exterior angle]

Hence \( \scriptsize \hat{PSQ} = 68^o \: – \: 40^o \)

Hence \( \scriptsize \hat{PSQ} = 28^o  \)

Step 2:

\( \scriptsize \hat{QRP} = \hat{PSQ} = 28^o \)

[Angles in the same segment]

\( \scriptsize \hat{QRP} = 28^o \)

Step 3:

\( \scriptsize \hat{QRS} = \hat{PSQ} = 74^o \)

But

\( \scriptsize \hat{QRS} = \hat{QRP} \: + \: \hat{PRS}  \) \( \scriptsize  \hat{PRS} = 74^o  \: – \: 28^o \) \( \scriptsize  \hat{PRS} =46^o \)

Question 4a

By how much is the sum of \( \scriptsize 3 \frac{1}{2} \) and \( \scriptsize 2 \frac{1}{5} \) less than 7

Step 1:

Determine the sum of \( \scriptsize 3 \frac{1}{2} \) and \( \scriptsize 2 \frac{1}{5} \)

⇒ \( \scriptsize 3 \frac{1}{2} \: + \:  \scriptsize 2 \frac{1}{5} \)

= \( \frac{11}{3} \: + \:  \frac{11}{5} \)

= \(  \frac{55 \: + \: 33}{15}  \)

= \(  \frac{88}{15}  \)

Step 2: Find the difference between 7 and \(  \frac{88}{15}  \)

\( \frac{7}{1} \: – \:  \frac{88}{15}  \)

\(  \frac{105 \: -\: 88}{15}  \)

\(  \frac{17}{15}  \)

= \(\scriptsize 1 \frac{2}{15}  \)

Question 4b

(b) The height, hm, of a clock above sea level is given by h = 6 + 4Cos (15P)°; 0< p < 6

Find:

(i) The value of h when p = 4

(ii) Correct to two significant figures, the value of p when h = 9m

Solution

Step 1: h = 6 + 4Cos (15p)0

(i) Substitute p = 4

h = 6 + 4Cos (15 x 4)0

h = 6 + 4Cos600

h = 6 + (4 x 0.5)

h = 6 + 2

h = 6m

Step 2: Substitute h = 9m into h = 6 + 4Cos (15p)0

  9 = 6 + 4 Cos (15p)0

9 – 6 = 4 Cos (15p)0

3 = 4 Cos (15p)0

Cos (15p)0 = \(  \frac{3}{4} \)

Cos (15p)0 = 0.75

15p0 = Cos-1 (0.75)

15p0 = 41.40

p0 = \(  \frac{41.40}{15} \)

p0 =2.760

p0 =2.8

Question 5

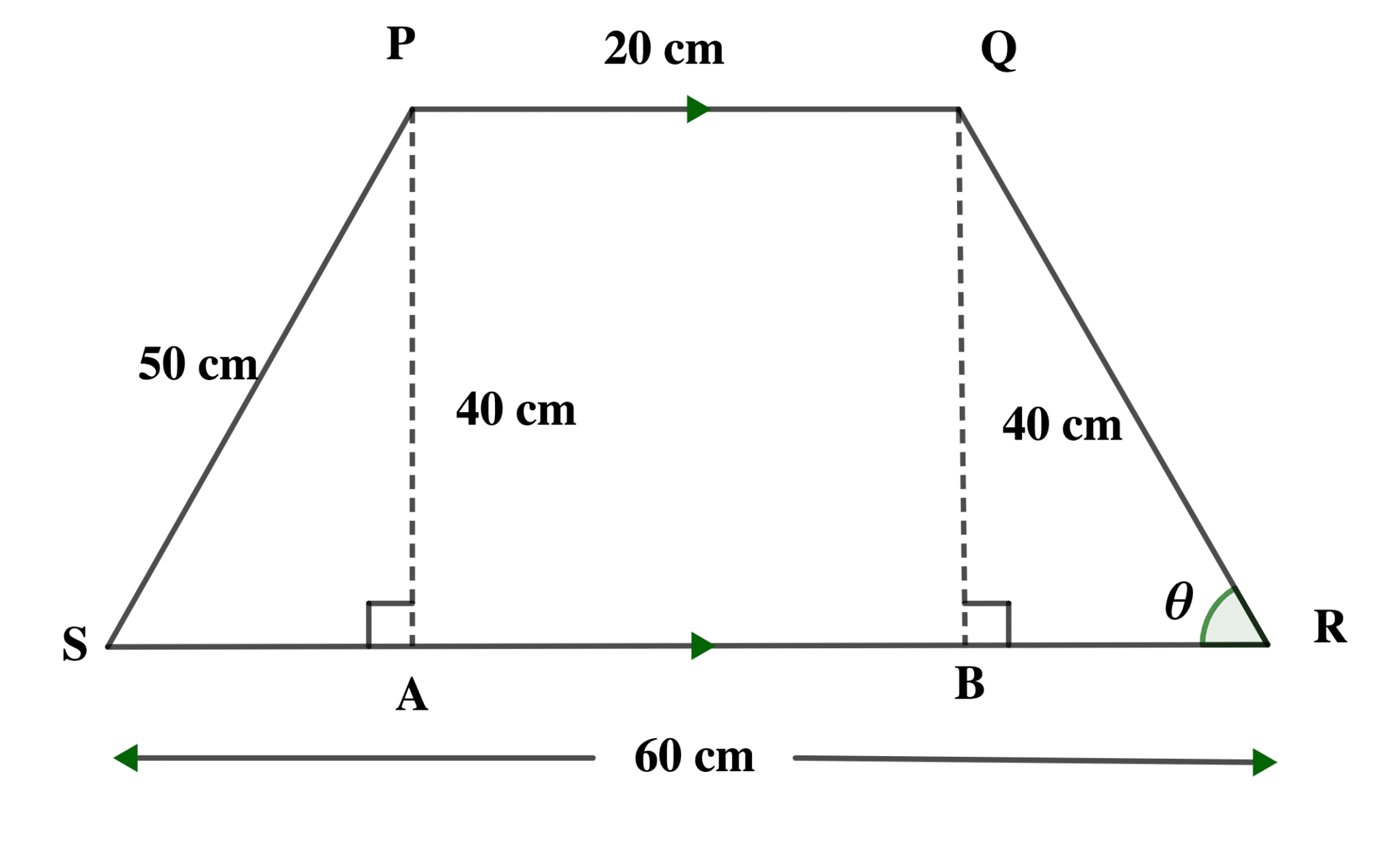
 A trapezium PQRS is such that PQ//RS and the perpendicular from P to RS is 40cm. If |PQ| = 20cm, |SP| = 50cm and |SR| = 60cm. calculate, correct to 2 significant figures, the:

(a) Area of the trapezium

Solution

Step 1: We first sketch the diagram

Step 2: State the formula for the area of a trapezium

Area = \( \frac{1}{2} \scriptsize (a \: + \: b) h \)

Area = \( \frac{1}{2} \scriptsize (20 \: + \: 60) 40 \)

= \( \frac{1}{2} \scriptsize 80 \: \times \:  40 \)

= 1600cm2

(b) <QRS

Solution

Step 1: Consider  PAS

|SA|2 = 502 – 402

|SA|2 = 2500 – 1600

|SA|2 = 900

|SA| = √900

|SA|= 30cm

Step 2: From the diagram

|BR| = 60 – 30 – 20

|BR| = 10cm

Step 3: Consider  QBR

i.e.

Let < QRS =  θ

tan θ = \( \frac{40}{10} \)

tan θ = 4

θ = tan-1 (4)

θ  = 75.96

θ =  760

Question 6a

(a). (i) Illustrate the following statement in a Venn diagram; All good literature students in a school are in the General Arts class.

(ii) Use the diagram to determine whether or not the following are valid conclusions from the given statement.

(1) Vivian is in the General Arts class, therefore, she is a good literature student.

(2). Audu is not a good Literature student therefore he is not in the General Arts class.

(3) Kweku is not in the General Arts class therefore he is not a good Literature student.

 

a(i) Solution

Step 1: Let; A and B represents

A = {all good literature students in the school}

B = {all students in the General Arts class}

Step 2: The Venn diagram representing the statement “All good literature students in a school are in the General Arts class” is shown below.

Where u = the students in the school

6a. (ii)

1 – Invalid statement {This is an invalid statement because there are some students in the General Arts class who are not good literature students}.

2 – Invalid statement. [This is also an invalid statement because it is not only good literature students that are in the General Arts class]

3 – This is a valid statement [This is because all good literature students are in the General Arts class]

Question 6b

(b). The cost (c) of producing n bricks is the sum of a fixed amount, h, and a variable amount y, where y varies directly as n. If it costs GH¢ 950.00 to produce 600 bricks and GH¢ 1,030.00 to produce 1000 bricks.

(i) Find the relationship between c, h, and n ;

(ii) Calculate the cost of producing 500 bricks.

6 b (i)

Step 1: Transforming this word problem into a mathematical statement we have

\( \scriptsize y \propto n \)

y = n k (where k = constant)

Step 2: Furthermore,

c = h + y ………….. (*)

Substituting y = n k in equation (*)

  c = h + n k

Step 3: if c = 950, n = 600

  950 = h + 600k ………………. (1)

Similarly if c = 1,030, n = 1000

  1,030 = h + 1000k ……………. (2)

Step 4: Solving equations (1) and (2) simultaneously (subtract (2) from (1)

950 = h + 600k

1,030 = h + 1000k

 -80 = – 400k

k = \( \frac{-80}{-400} \)

k = \( \frac{1}{5} \)

Step 5: Substitute k = \( \frac{1}{5} \)

into equation (1)

950 = h + 600 x \( \frac{1}{5} \)

950 = h + 120

  h = 950 – 120

  h = 830

Hence the relationship between c, h and n is

\( \scriptsize c = 830 \: + \: \normalsize \frac{1}{5} \scriptsize n \)

6b (ii)

Step 1: \( \scriptsize c = 830 \: + \: \normalsize \frac{1}{5} \scriptsize n \)

If n = 500

\( \scriptsize c = 830 \: + \:  \left( \normalsize \frac{1}{5} \scriptsize \: \times \: 500 \right) \)

C = 830 + 100

C = GH¢ 930.00

Question 7

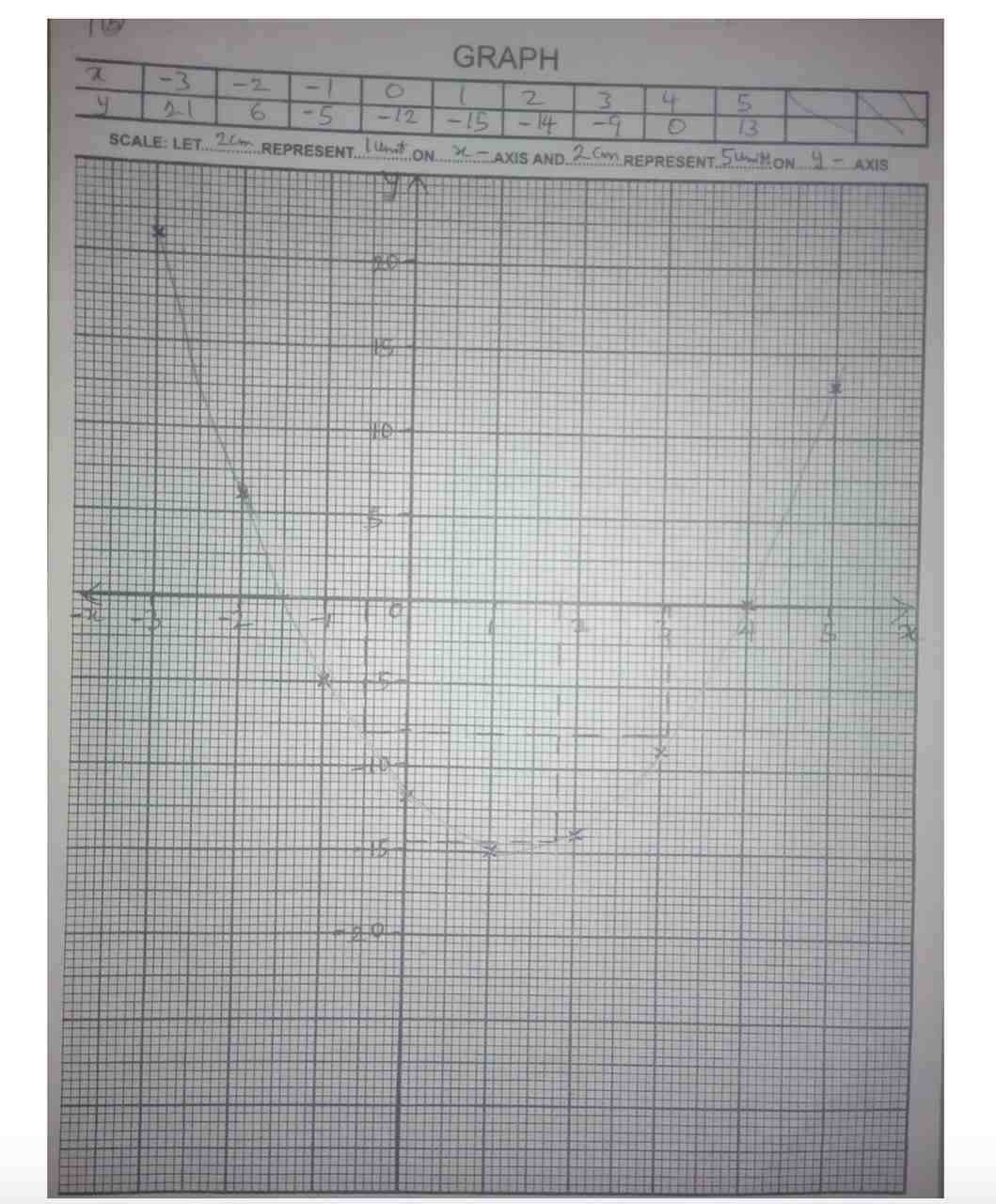
The table is for the relation y = px2 – 5x + q

x

-3

-2

-1

0

1

2

3

4

5

y

21

6

-12

0

13

(a) (i) use the table to find the values of p and q

(ii) Copy and complete the table

(b) Using scales of 2cm to 1 unit on the x-axis and 2cm to 5 units on the y –axis, draw the graph of the relation for \( \scriptsize -3 \leq x \leq 5 \)

(c) Use the graph to find x when

(i) y when x = 1.8

(ii) y = -8

Solution

a(i)

Step 1: from the table when x = -3, y = 21 substitute in

y  = p x2 – 5x + q

  21 = p(-3)2 – 5 (-3) + q

21 = 9p + 15 + q

6  = 9p + q

Step 2: Similarly when x = 4, y = 0, substitute this in the relation.

  0 = p (4)2 – 5(4) + q

0 = 16p – 20 + q

20 = 16p + q ………… (2)

Substitute p = 2 in equation (1)

  6 = 9(2) + q

6 – 18 = q

    q  = -12

  p = 2 and q = -12

The relation is

y = 2x2 – 5x – 12

Step 1: To copy and complete the table we set out the table as shown below

x

-3

-2

-1

0

1

2

3

4

5

2x2

18

8

2

0

2

8

18

32

50

-5x

15

10

5

0

-5

-10

-15

-20

-25

-12

-12

-12

-12

-12

-12

-12

-12

-12

-12

y

21

6

-5

-12

-15

-14

-9

0

13

7c. (i) y when x = 1.8 from the graph trace from where x = 1.8, to the graph then to the y – axis. From the graph y = -14.5

(ii) x when y = -8 from the graph, the values of x when y = -8 are x = -0.5 or 3.1

Question 8

(a). Using ruler and a pair of compasses only, construct a:

(i) Trapezium WXYZ such that |WX| = 8cm, |XY| = 5.5cm, |XZ| = 8.3cm, < WXY = 600 and WX||ZY

(ii)Rectangle PQYZ where P and Q are on WX.

(b) measure: (i) |QX| (ii) <XWZ

Solution

(a)(i) To construct the trapezium WXYZ

Step 1: Draw |WX| = 8cm

Step 2: Construct angle 600 at x to face side WT

Step 3: Draw an arc of radius 8.5cm to locate point Y

Step 4: Draw an arc of radius 8.3cm with centre X, to locate Z

Step 5: Join YZ and WZ to complete the trapezium WXYZ

Step 6: Draw the perpendiculars |PZ| and |QY| to pass through Z and Y respectively

Step 7: Measure (i) |QX|

(ii) <XWZ

8b. (i) |QX| = 3CM

(ii)  \( \scriptsize \hat{XWZ} \) = 770

Question 9

(a) The first term of an Arithmetic progression (AP) is -8, the ratio of the 7th term to the 9th term is 5:8, find the common difference of the A.P.

Solution

Step 1: State the formula for the nth term of an A.P

Tn = a + (n – 1) d

a  = -8 (given)

Step 2: Form expressions for the 7th and 9th terms.

  T7 = -8 + (7 – 1)d

T7 = -8 + 6d

Also T9 = -8 + (9 – 1)d

T9 = -8 + 8d

Step 3: But 7th: 9th term = 5: 8

(given)

  (-8 + 6d) : (-8 + 8d) = 5:8

\( \frac{-8 \: + \: 6d}{-8 \: + \: 8d} = \frac{5}{8} \)

8(-8 + 6d) = 5(-8 + 8d)

-64 + 48d = -40 + 40d

48d – 40d = -40 + 64

8d = 24

d = \( \frac{24}{8} \)

d = 3

Question 9b

A trader bought 30 baskets of pawpaw and 100 baskets of mangoes for N2450.00. She sold the pawpaw at a profit of 40% and the mangoes at a profit of 30%. If her profit on the entire transaction was 855.00, find the:

(i) cost price of a basket of pawpaw;

(ii) selling price of the 100 baskets of mangoes.

Step 1: Let the cost price of the 30 baskets of pawpaw = Nx

Then the cost price (C.P) of the 100 baskets of mangoes = N(2450 – x)

Step 2: Determine the profit made on each fruit

Profit made on pawpaw = \( \frac{4}{100} \scriptsize \: \times \: x = 0.4x \)

Profit made on mangoes = \( \frac{4}{100} \scriptsize \: \times \: (250 \: -\: x) = 0.3(250 \: -\: x) \)

Step 3: The entire profit made is N855 (given)

  855 = 0.4x + 0.3 (2450 – x)

855 = 0.4x + 735 – 0.3x

855 – 735 = 0.4x – 0.3x

120 = 0.1x

x = \( \frac{120}{0.1} \)

x = 1200 

(i) Hence the cost price of a basket of pawpaw = \( \frac{1200}{0.3} \)

= N40.00

(ii) Step 1: Profit made on the baskets of mangoes sold = 0.3 (2450 – x)

= 0.3 (2450 – 1200)

= 0.3 x 1250

= N375

Step 2: Therefore the selling price of the 100 baskets of mangoes = (N2450 – N1200) + N375

= N1250 + N375

= N1625

Question 10

(a) Without using mathematical tables or calculators, simplify:

\( \frac{2 tan 60^0 \: + \: cos30^o}{sin 60^o} \)

Step 1: Write the trigonometric ratios in surd form

\( \frac{2 tan 60^0 \: + \: cos30^o}{sin 60^o} = \frac{2 \sqrt{3} \: + \: \frac{\sqrt{3}}{2}}{\frac{\sqrt{3}}{2}} \)

= \( \frac{2 \sqrt{3}}{\frac{\sqrt{3}}{2}} \: + \: \frac{\frac{\sqrt{3}}{2}}{\frac{\sqrt{3}}{2}} \)

= \( \frac{2 \sqrt{3}}{1} \: \times \: \frac{2}{\sqrt {3}}  \scriptsize \: + \: 1\)

= 4 + 1

= 5

Question 10b

From an aeroplane in the air and at a horizontal difference of 1050m, the angles of depression of the top and base of a control tower at an instance are 36º and 41º respectively. Calculate, correct to the nearest meter, the:

(i) Height of the control tower

(ii) Shortest distance between the aeroplane and the base of the control tower.

Step 1: Sketch the diagram

Step 2: The height of the Tower is represented in the diagram by |BC| = |AE|

Step 3: Consider  ΔBAD

Tan 410 = \( \frac{AD}{1050} \)

AD = 1050 x Tan 410

|AD| = 912.75

Step 4: Consider  ΔCED

Tan 360 = \( \frac{DE}{EC} \)

Tan 360 = \( \frac{DE}{1050} \)

[EC = AB]

DE = 1050 x tan 360

DE = 762.86

Step 5: the height of the control tower BC = AE

|AE| = |AD| – |DE|

|AE| = 912.75 – 762.86

    = 149.89

= 150m (correct to the nearest metres)

(ii) The shortest distance between the aeroplane and the base of the tower is represented by |BD| in the diagram

From ΔBAD

Sin 410 = \( \frac{AD}{BD} \)

Sin 410 = \( \frac{912.75}{BD} \)

BD = \( \frac{912.75}{Sin 41^o} \)

|BD| = 1,391.26

|BD| = 1,391m (to the nearest meter)

Question 11a

Make m the subject of the relations

h = \( \frac{mt}{d(m \: + \: p)} \)

Solution

Step 1: Multiply both sides by d(m + p)

h x d (m + p) = \( \frac{mt}{d(m \: + \: p)} \: \times \: \frac{d(m \: + \: p)}{1}\)

Step 2: Simplifying this, we have

hd (m + p) = mt

hdm + hdp = mt

hdp = mt – hdm

hdp = m (t – hd)

m = \( \frac{hdp}{m(t \: -\: hd)} \)

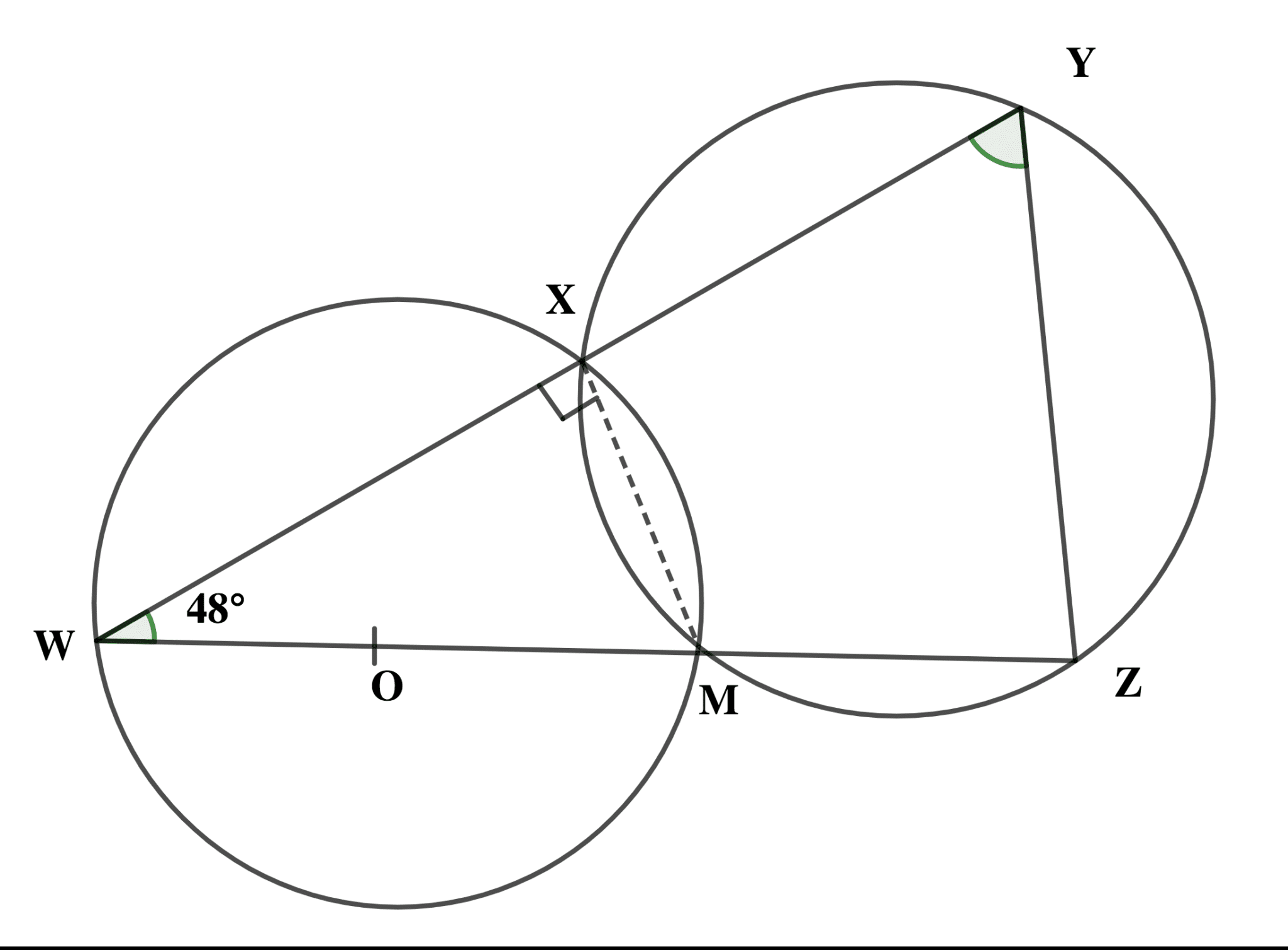
Question 11b

In the diagram, WY and WZ are straight lines, O is the centre of circle WXM  and <XWM = 480. Calculate the value of <WYZ.

 

Step 1: Produce x to m, or join x to m.

\(\scriptsize \hat{WXM} \) = 900 (angle in a semi circle)

Step 2:

\(\scriptsize \hat{XWM} \: +\:  \hat{WXM} \: +\:  \hat{WMX} = 180^o \)

(sum of angles in a triangle)

\(\scriptsize 48^o \: +\:  90^o \: +\:  \hat{WMX} = 180^o \) \(\scriptsize   \hat{WMX} = 180^o \: -\: 138^o \)

Step 3: But \(\scriptsize   \hat{XMZ} = 180^o \: -\:  \hat{WMX} \)

(sum of angles on a straight line)

\(\scriptsize   \hat{XMZ} = 180^o \: -\:  42^0 \) \(\scriptsize   \hat{XMZ} = 138^0 \)

Step 4: Hence \(\scriptsize   \hat{WYZ}  \: +\: \hat{XMZ}= 180^0 \)

(opposite angles of a cyclic quadrilateral)

\(\scriptsize  \hat{XMZ}= 180^0 \: – \:  130^0\) \(\scriptsize  \hat{XMZ}= 42^0\)

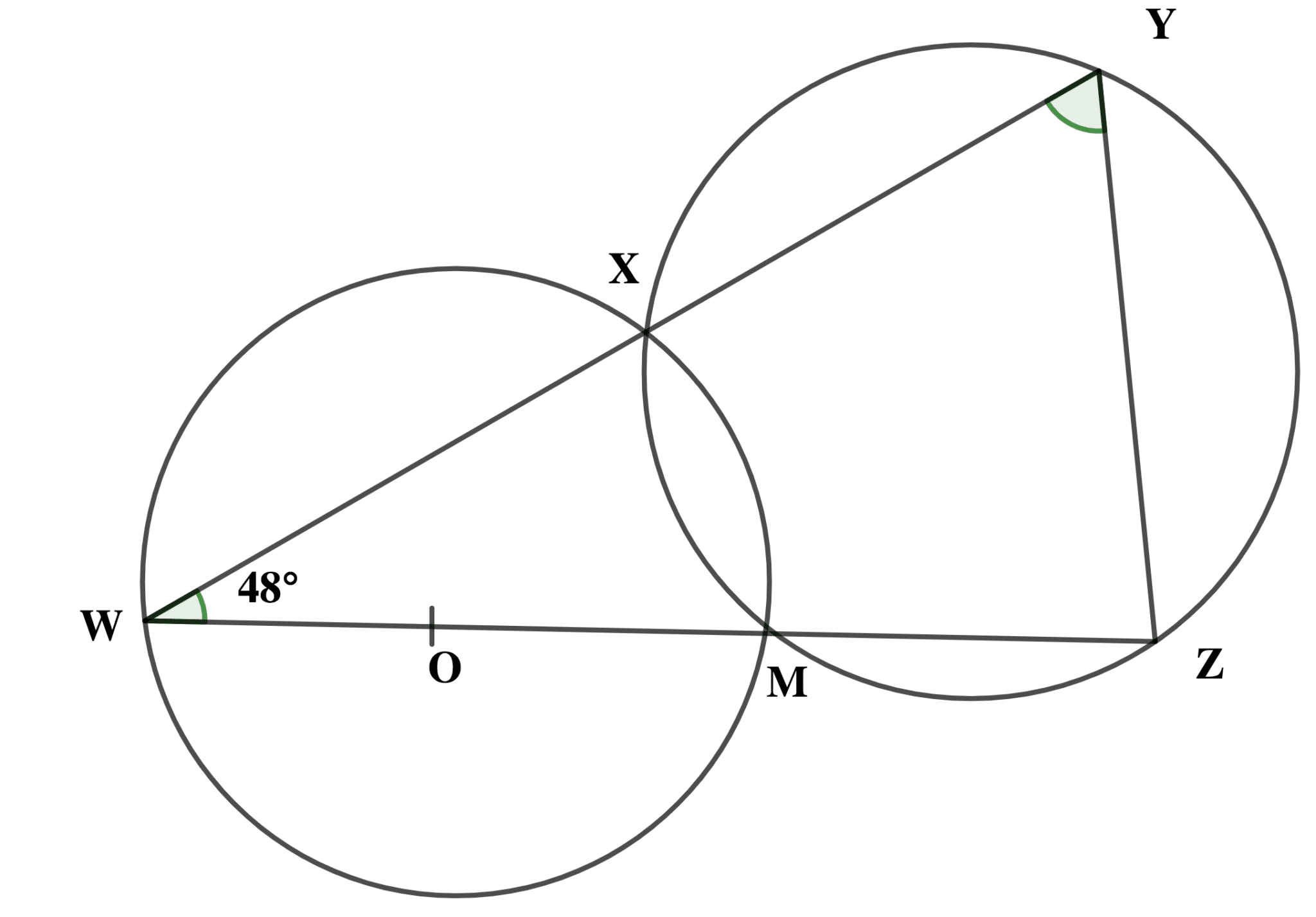
Question 11c

An operation is defined on the set X = {1,3,5,6} by  \( \scriptsize  m \bigotimes n  \)  = m + n + 2 (mod 7), where m, n EX

(i) Draw a table for the operation

(ii) Using the table, find the truth set of:

\( \scriptsize 3 \bigotimes n = 3  \)

\( \scriptsize n \bigotimes n = 3  \)

i) Step 1: We set out table for the operation

m \( \scriptsize \ast \) n = m + n + 2 (mod 7) on the set X = {1, 3, 5, 6} as shown below.

\( \scriptsize \bigotimes \) 1 3 5 6
1 4 6 1 2
3 6 1 3 4
5 1 3 5 5
6 2 4 6 0

iii. from the table

\( \scriptsize 3 \bigotimes n = 3 \),  the truth set of n from the table is {5}.

\( \scriptsize n \bigotimes n = 3 \) From the table the truth set of n is { }  or empty set.

Question 12

A water reservoir in the form of a cone mounted on a hemisphere is built such that the plane face of the hemisphere fits exactly to the base of the cone and the height of the cone is 6 times the radius of its base.

(a) Illustrate this information in a diagram

(b) If the volume of the reservoir is \( \scriptsize 333 \frac{1}{3} \pi m^3 \), calculate correct to the nearest whole number, the:

(i) Volume of the hemisphere:

(ii) Total surface area of the reservoir.

[Take π = \( \frac{22}{7} \) ]

Step 1: (i) the volume of the reservoir = \( \scriptsize 333 \frac{1}{3} \pi m^3 \) Given

But by formula, the volume = volume of the cone + volume of the hemisphere.

Step 2: Volume of cone = \(\frac{1}{3} \scriptsize \pi r^3 h \)

Volume of the hemisphere = \(\frac{1}{2} \: \times \: \frac{4}{3} \scriptsize \pi r^3 h \)

Volume of the hemisphere = \( \frac{2}{3} \scriptsize \pi r^3 h \)

\( \scriptsize 333 \frac{1}{3} \pi   =  \normalsize \frac{1}{3} \scriptsize \pi r^3 h\: + \:  \normalsize  \frac{2}{3} \scriptsize \pi r^3 h \)

\( \normalsize  \frac{1000}{3} \scriptsize \pi   =  \normalsize \frac{1}{3} \scriptsize \pi  \left (\scriptsize 2r^3 \: +\: r^2h \right )\)

Let the radius of the hemisphere be x m;

\(  \frac{1000}{3} =  \normalsize \frac{1}{3} \scriptsize  \left (\scriptsize 2x^3 \: +\: x^2(6x) \right )\)

\(  \scriptsize 1000 = 2x^3 \: +\: 6x^3 \)

\(  \scriptsize 1000 = 8x^3 \)

\(  \scriptsize x^3 = \normalsize \frac{1000}{8} \)

\(  \scriptsize x^3 = 125 \)

\(  \scriptsize x = \sqrt[3]{125}\)

\(  \scriptsize x = 5m\)

Step 3: The volume of the hemisphere is obtained from the formula

Volume = \( \frac{2}{3} \scriptsize \pi r^3 \)

Volume = \( \frac{2}{3} \: \times \: \frac{22}{7} \scriptsize \: \times \: 5^3 \)

= \( \frac{5500}{21} \)

= 261.90

= 262m (to the nearest whole number)

(iii) Step 1: Total surface area of the reservoir = curved surface area of the cone + surface area of the hemisphere

Total surface area = \( \scriptsize \pi r l \: + \: \normalsize \frac{1}{2} \scriptsize \: \times \: 4 \pi r^2 \)

Total surface area = \( \scriptsize \pi r l \: + \: 2 \pi r^2 \)

Step 2: To obtain the value of  l, we consider the triangle below

\( \scriptsize l^2 = 30^2 \: + \: 5^2 \) \( \scriptsize l^2 = 900 \: + \: 25 \) \( \scriptsize l^2 = 925 \) \( \scriptsize l = \sqrt{925} \) \( \scriptsize l = 30.41m \)

Step 4: Therefore;

T.S. = \( \frac{22}{7} \left [\scriptsize  (5 \: \times \: 3.041) \: + \: (2 \: \times \: 5^2)  \right ] \)

T.S. = \( \frac{22}{7} \left [\scriptsize   152.05 \: + \: 50  \right ] \)

T.S. = \( \frac{22}{7}  \: \times  \: \frac{202.05}{1}\)

T.S. = \( \frac{4445.1}{7}  \)

T.S. = 635.01

T.S. = 635m2 (nearest whole number)

Question 13

The table shows the marks scored by some candidates in an examination

Mark %

0-9

10-19

20-29

30-39

40-49

50-59

60-69

70-79

80-89

90-99

Frequency

7

11

17

20

29

34

30

25

21

6

(a) Construct a cumulative frequency table for the distribution and draw a cumulative frequency curve

(b) Use the curve to estimate, correct to one decimal place, the;

(i) Lowest mark for distinction if 5% of the candidates passed with distinction

(ii)Probability of selecting a candidate who scored at most 45%.

Solution

Step 1: We construct the cumulative frequency table as shown below:

Marks %

Frequency (F)

Cumulative frequency

Upper-class boundaries

0 – 9

7

7

9.5

10 – 19

11

18

19.5

20 – 29

17

35

29.5

30 – 39

20

55

39.5

40 – 49

29

84

49.5

50 – 59

34

118

59.5

60 – 69

30

148

69.5

70 – 79

25

173

79.5

80 – 89

21

194

89.5

90 – 99

6

200

99.5

Step 2: The cumulative frequency curve is constructed, using the vertical axis (y-axis) for the cumulative frequency and the horizontal axis (x-axis) for the upper-class boundaries.

13b. Step 1: If 5% of the candidate posed with distinction, then we obtain the number from the calculation below:

\( \frac{5}{100} \: \times \: \frac{200}{1} \)

= 5 x 2 = 10

That mean, just 10 candidates have distinction.

Step 2: To determine the lowest mark for distinction we carry out the computation as follows:

(200 – 10) = 190

Step 3: We then go to the cumulative frequency axis, locate where we have 190, then trace it to the graph

 =  87%.

13b. (ii) To determine the required probability

Step 1: We first find the number of candidates that scored at most 45%

Step 2: We can trace this out from the graph. From the x-axis to the graph, then to the y-axis. This is indicated on the graph with broken lines.

From the graph, the value is 70 (point labelled B)

Step 3: The probability = \( \frac{70}{200} \)

= 0.35

Report

Harassment or bullying behavior
Contains mature or sensitive content
Contains misleading or false information
Contains abusive or derogatory content
Contains spam, fake content or potential malware

Block Member?

Please confirm you want to block this member.

You will no longer be able to:

  • See blocked member's posts
  • Mention this member in posts
  • Invite this member to groups
  • Message this member
  • Add this member as a connection

Please note: This action will also remove this member from your connections and send a report to the site admin. Please allow a few minutes for this process to complete.

Report

You have already reported this .
error: Alert: Content selection is disabled!!