WAEC: MATHEMATICS
Quizzes
-
2021 Mathematics WAEC Objective Past Questions
-
2021 Mathematics WAEC Essay Past Questions
-
2020 Mathematics WAEC Objective Past Questions
-
2020 Mathematics WAEC Theory Past Questions
-
2019 Mathematics WAEC Objective Past Questions
-
2019 Mathematics WAEC Theory Past Questions
-
2018 Mathematics WAEC Objective Past Questions
-
2018 Mathematics WAEC Theory Past Questions
-
2017 Mathematics WAEC Objective Past Questions
-
2017 Mathematics WAEC Theory Past Questions
-
2016 Mathematics WAEC Objective Past Questions
-
2016 Mathematics WAEC Theory Past Questions
-
2015 Mathematics WAEC Objective Past Questions
-
2015 Mathematics WAEC Theory Past Questions
-
2014 Mathematics WAEC Objective Past Questions
-
2014 Mathematics WAEC Theory Past Questions
Quiz Summary
0 of 13 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 13 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 13
1. Question
(a) If (y−1)log104 = ylog1016, without using Mathematics tables or calculator, find the value of y.
(b) When I walk from my house at 4km/h, I will get to my office 30mins later than when I walk at 5km/h. Calculate the distance between my house and office.
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 2 of 13
2. Question
(a) Solve the equation: \( \normalsize \frac{2}{3} \scriptsize (3x \: -\:5) \: – \: \normalsize \frac{3}{5} \scriptsize (2x \: -\: 3) = 3 \)
(b) In the diagram, < STQ = m, < TUQ = 80°, < UPQ = r, < PQU = n and < RQT = 88°. Find the value of (m + n).
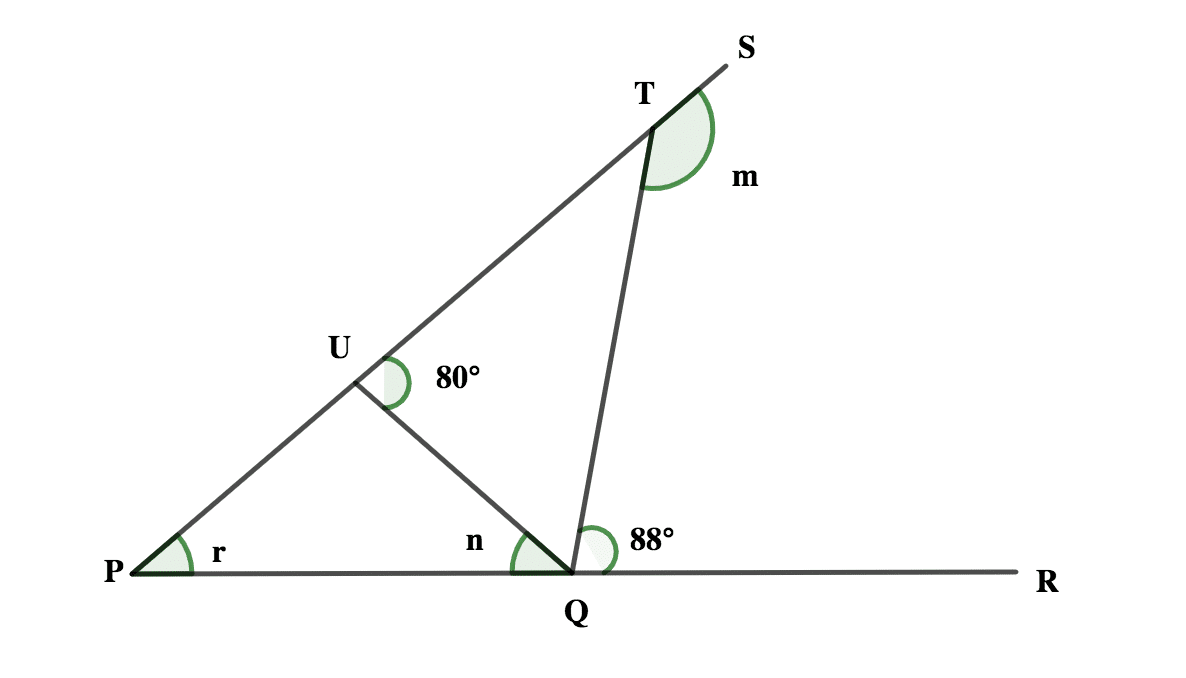
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 3 of 13
3. Question
(a) The angle of depression of a point P on the ground from the top T of a building is 23.6º. If the distance, from P to the foot of the building is 50m, calculate, correct to the nearest metre, the height of the building.
(b)In the diagram, PT||SU, QS||TR, |SR| = 6cm and |RU| = 10cm. If the area of ΔTRU = 45cm2, Calculate the area of trapezium QTUS.
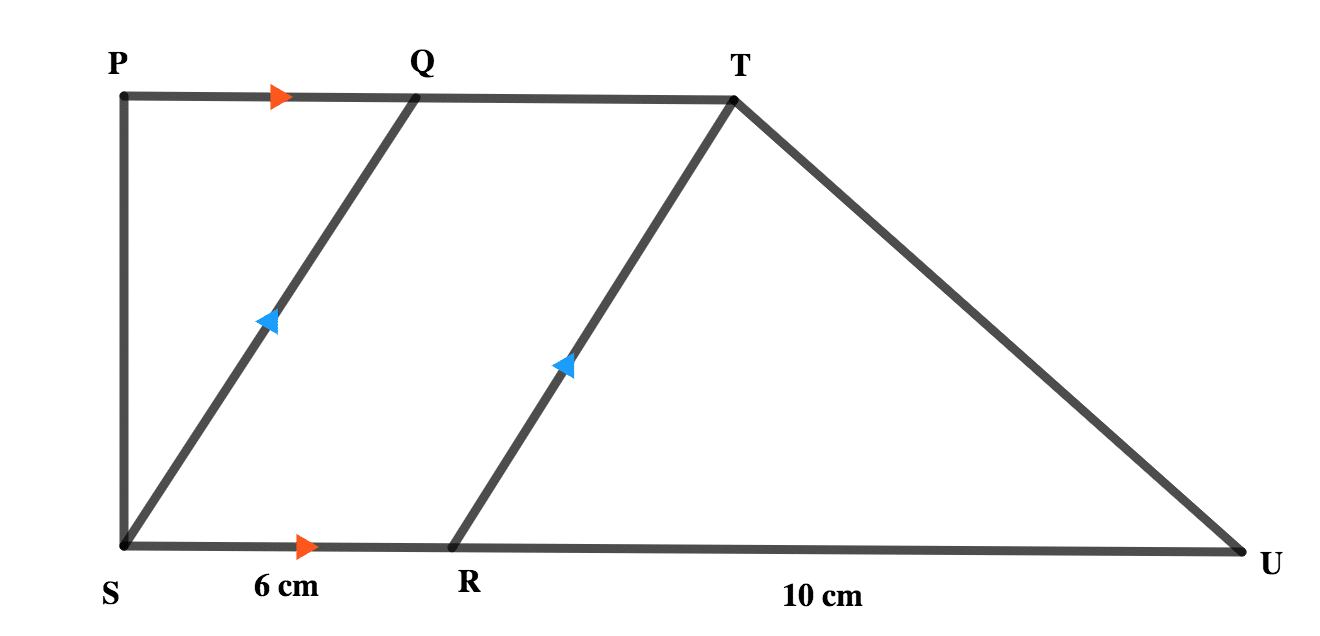
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 4 of 13
4. Question
If the sixth term of an Arithmetic Progression (A.P) is 37 and the sum of the first six terms is 147, find the
a. First term
b. Sum of the first fifteen terms
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 5 of 13
5. Question
Out of 120 customers in a shop 45 bought both bags and shoes. If all the customers bought either bags or shoes and 11 more customers bought shoes than bags:
a. Illustrate this information in a diagram
b. Find the number of customers who bought shoes:
c. Calculate the probability that a customer selected at random bought bags.
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 6 of 13
6. Question
a. A manufacturing company requires 3 hours of direct labour to process every N87.00 worth of raw materials. If the company uses N30,450.00 worth of raw materials, what amount should it budget for direct labour at N18.25 per hour?
b. An investor invested Nx in bank M at the rate of 6% simple interest per annum and Ny in bank N at the rate of 8% simple interest per annum. If a total of N8,000,000.00 was invested in two banks and the investor received a total of N2,320,000.00 as interest from the two banks after 4 years, calculate the
(i). Values of x and y
(ii) Interest paid by the second bank
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 7 of 13
7. Question
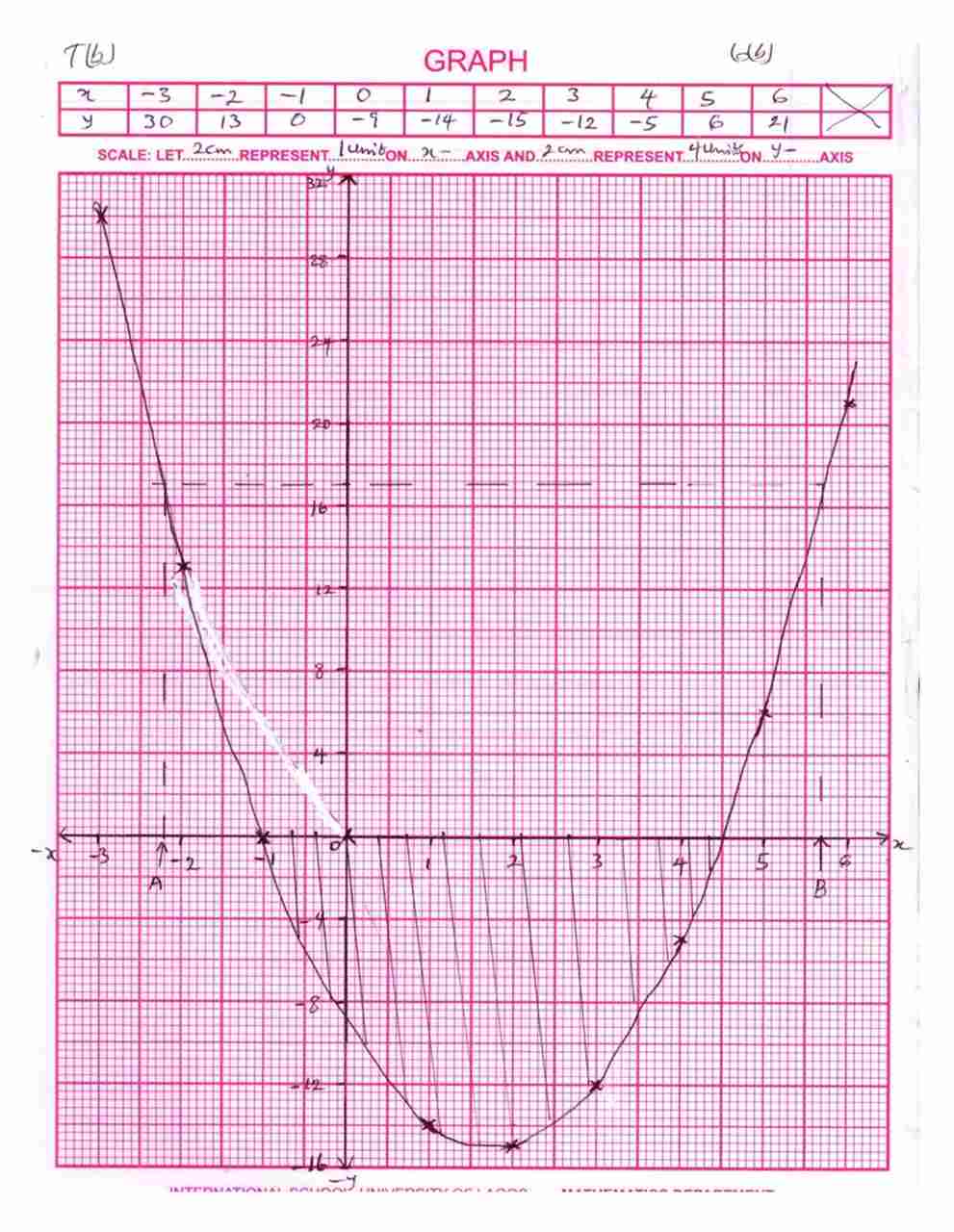
a. Copy and complete the table of values for the equation
y = 2x2 – 7x – 9 for -3 ≤ x ≤ 6
x
-3
-2
-1
0
1
2
3
4
5
6
y
13
-9
-14
-12
6
(b) Using scales of 2cm to 1 unit on the x-axis and 2cm to 4 units on the y – axis, draw the graphs of
y = 2x2 – 7x – 9 for -3 ≤ x ≤ 6
(c) Use the graph to estimate the
(i) roots of the equation 2x2 – 7x = 26
(ii) coordinates of the minimum point of y;
(iii) range of values for which 2x2 – 7x < 9.
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 8 of 13
8. Question
Marks 1 2 3 4 5 Number of students m+2 m-1 2m-3 m+5 3m-4 The table shows the distribution of marks scored by some students in a test.
(a) If the mean mark is \( \scriptsize 3\frac{6}{23} \), find the value of m
(b) Find the
i. Interquartile range
ii. Probability of selecting a student who scored at least 4 marks in the test.
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 9 of 13
9. Question
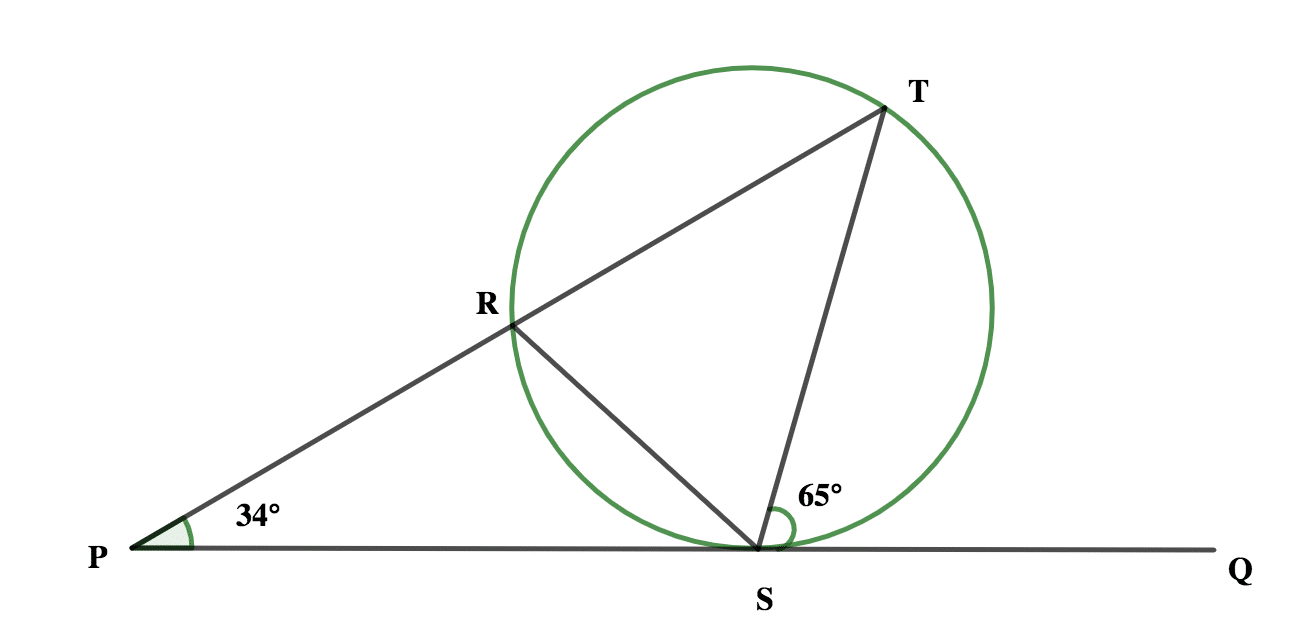
(a) PQ is a tangent to a circle RST at the point S. PRT is a Straight line, <TPS = 34º and <TSQ = 65º
(i) Illustrate the information in a diagram
(ii) Find the value of (a) <RTS (b) <SRP
(b) In the diagram, |VZ| = |YZ|, <YXZ = 200 and <ZVY = 520, calculate the size of <WYZ.

-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 10 of 13
10. Question
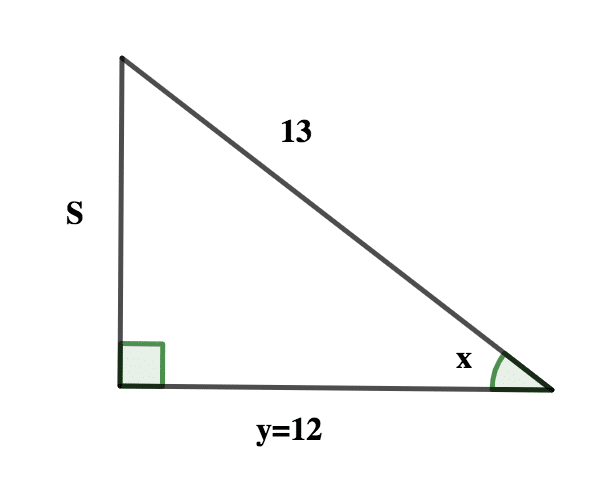
a. Given that Sin x = \( \frac{5}{13}\scriptsize, O^o < x < 90^o\)
Find \( \frac{cosx \: – \: 2 sinx}{2 tan x} \)
b. A ladder, LA, leans against a vertical pole at a point L which is 9.6meters above the ground. Another ladder, LB, 12 metres long, leans on the opposite side of the pole and at the same point L. If A and B are 10 metres apart and on the same straight line as the foot of the pole, calculate, correct to 2 significant figures, the;
(i) Length of ladder LA
(ii) angle which LA makes with the ground
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 11 of 13
11. Question
a. It takes 8 students two-thirds of an hour to fill 12 tanks with water. How many tanks of water will 4 students fill in one-third of an hour at the same rate?
b. A chord, 20cm long is 12cm from the centre of circle. Calculate, correct to one decimal place, the;
(i) Angle subtended by the chord at the centre of the circle;
(ii) Perimeter of the minor segment cut off by the chord. [Take π = 3.142]
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 12 of 13
12. Question
(a) Using completing the square method, solve, correct to 2 decimal places, the equation 3y2 – 5y + 2 = 0
(b) Given that
M = \( \scriptsize \begin{pmatrix}1& 2\\4& 3\end{pmatrix} \)
N = \( \scriptsize \begin{pmatrix}m& x\\n& y\end{pmatrix} \)
MN = \( \scriptsize \begin{pmatrix}2& 1\\3& 4\end{pmatrix} \)
Find the matrix N.
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 13 of 13
13. Question
(a) The operation (*) is defined on the set of real number, R, by
x (*) y = \( \frac{x \: +\: y}{2}\scriptsize ,\: x,\: y \: \epsilon \: R \)
(i) Evaluate \( \scriptsize 3 (\ast )\normalsize \frac{2}{5} \)
(ii) If \( \scriptsize 8(\ast )y = 8 \frac{1}{4}\)
find the value of y
(b)
In ΔABC,
\( \scriptsize \bar{AB} = \normalsize \binom{-4}{\:\:6} \)
\( \scriptsize \bar {AC} = \normalsize \binom{\:\:3}{-8} \)
If P is the midpoint of \( \scriptsize \bar{AB}\), express \( \scriptsize \bar{CP}\) as a column vector.
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -







Responses