WAEC: MATHEMATICS
Quizzes
-
2021 Mathematics WAEC Objective Past Questions
-
2021 Mathematics WAEC Essay Past Questions
-
2020 Mathematics WAEC Objective Past Questions
-
2020 Mathematics WAEC Theory Past Questions
-
2019 Mathematics WAEC Objective Past Questions
-
2019 Mathematics WAEC Theory Past Questions
-
2018 Mathematics WAEC Objective Past Questions
-
2018 Mathematics WAEC Theory Past Questions
-
2017 Mathematics WAEC Objective Past Questions
-
2017 Mathematics WAEC Theory Past Questions
-
2016 Mathematics WAEC Objective Past Questions
-
2016 Mathematics WAEC Theory Past Questions
-
2015 Mathematics WAEC Objective Past Questions
-
2015 Mathematics WAEC Theory Past Questions
-
2014 Mathematics WAEC Objective Past Questions
-
2014 Mathematics WAEC Theory Past Questions
Quiz Summary
0 of 13 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 13 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 13
1. Question
(a) If A = {multiples of 2}, B = {multiples of 3} and C = {factors of 6} are subsets of μ = {x: 1 ≤ x ≤ 10}, find \( \scriptsize A’ \cap B’ \cap C’ \)
(b) Tickets for a movie premiere cost $18.50 each while a bulk purchase price for 5 tickets is $80.00. If 4 gentlemen decide to get a fifth person to join them so that they can share the bulk purchase price equally, how much would each person save?
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 2 of 13
2. Question
(a) Given that P = \( \left ( \frac{rk}{Q} \: – \: ms\right)^{\frac{2}{3}} \)
(i) Make Q the subject of the relation;
(ii) Find, correct to two decimal places the value of Q when P = 3, m = 15, s = 0.2, k = 4 and r = 10
(b) Given that \( \frac{x \: + \: 2y}{5} \scriptsize = x \: – \: 2y \)
find x: y
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 3 of 13
3. Question
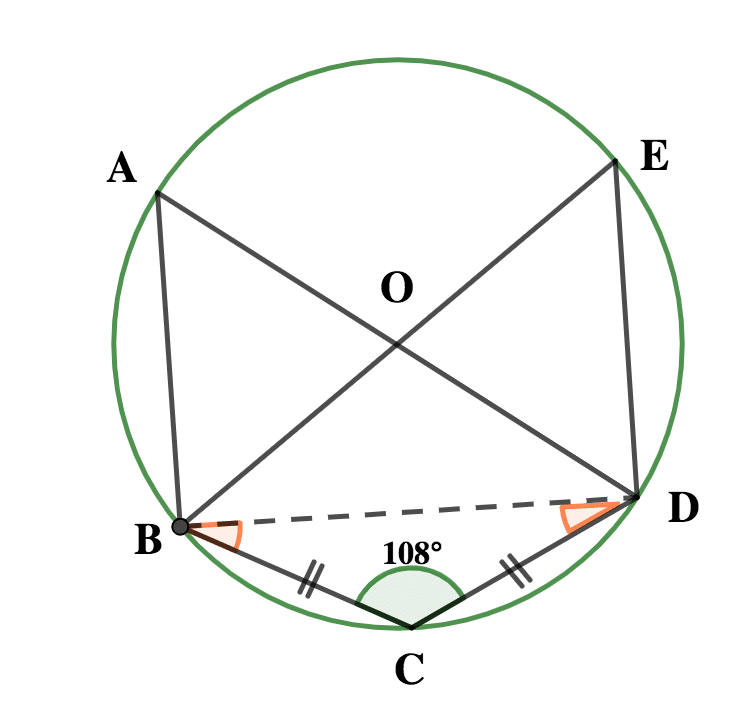
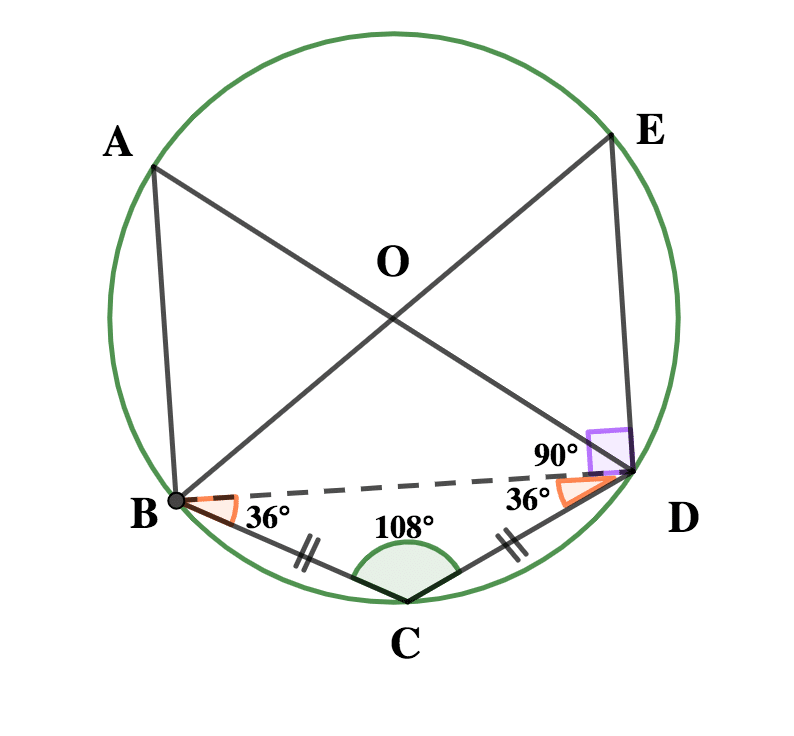
(a)
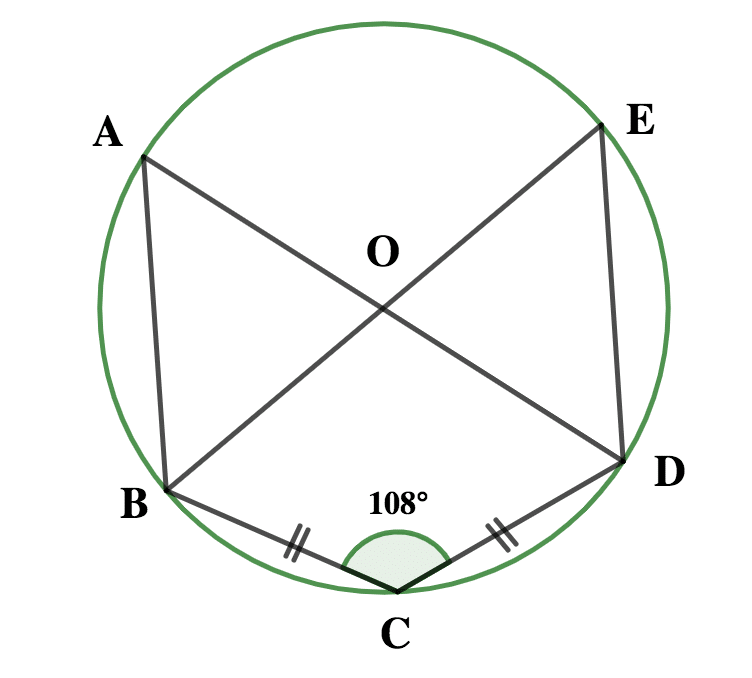
In the diagram, O is the centre of the circle ABCDE, \( \scriptsize \bar{|BC|} = \bar{|CD|} \) and ∠BCD = 108º. Find ∠CDE
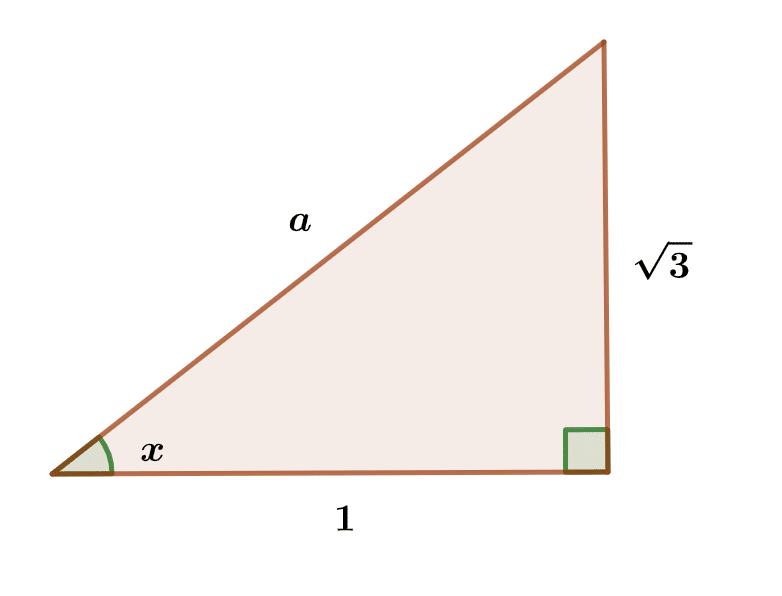
(b) Given that tan x = √3, \( \scriptsize \; \; \; \; 0^o \leq x \leq 90^o \)
Evaluate \( \frac{(cosx)^2 \: – \: sinx}{(sinx)^2 \: + \: cosx} \)
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 4 of 13
4. Question
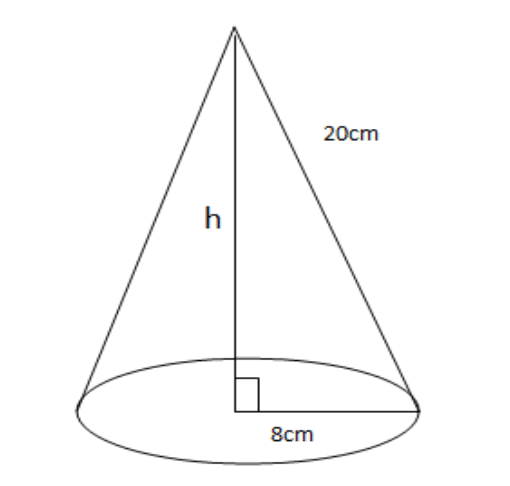
The total surface area of a cone of slant height 1 cm and base radius r cm is 224πcm2.
If r : l = 2 : 5, find:
(a) Correct to one decimal place, the value of r
(b) Correct to the nearest whole number, the volume of the cone
Take π = \( \frac{22}{7} \)
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 5 of 13
5. Question
A die was rolled a number of times. The outcomes are as shown in the table.
Number
1
2
3
4
5
6
outcomes
32
m
25
40
28
45
If the probability of obtaining 2 is 0.15, find the:
(a) Value of m;
(b) Number of times the die was rolled;
(c) Probability of obtaining an even number
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 6 of 13
6. Question
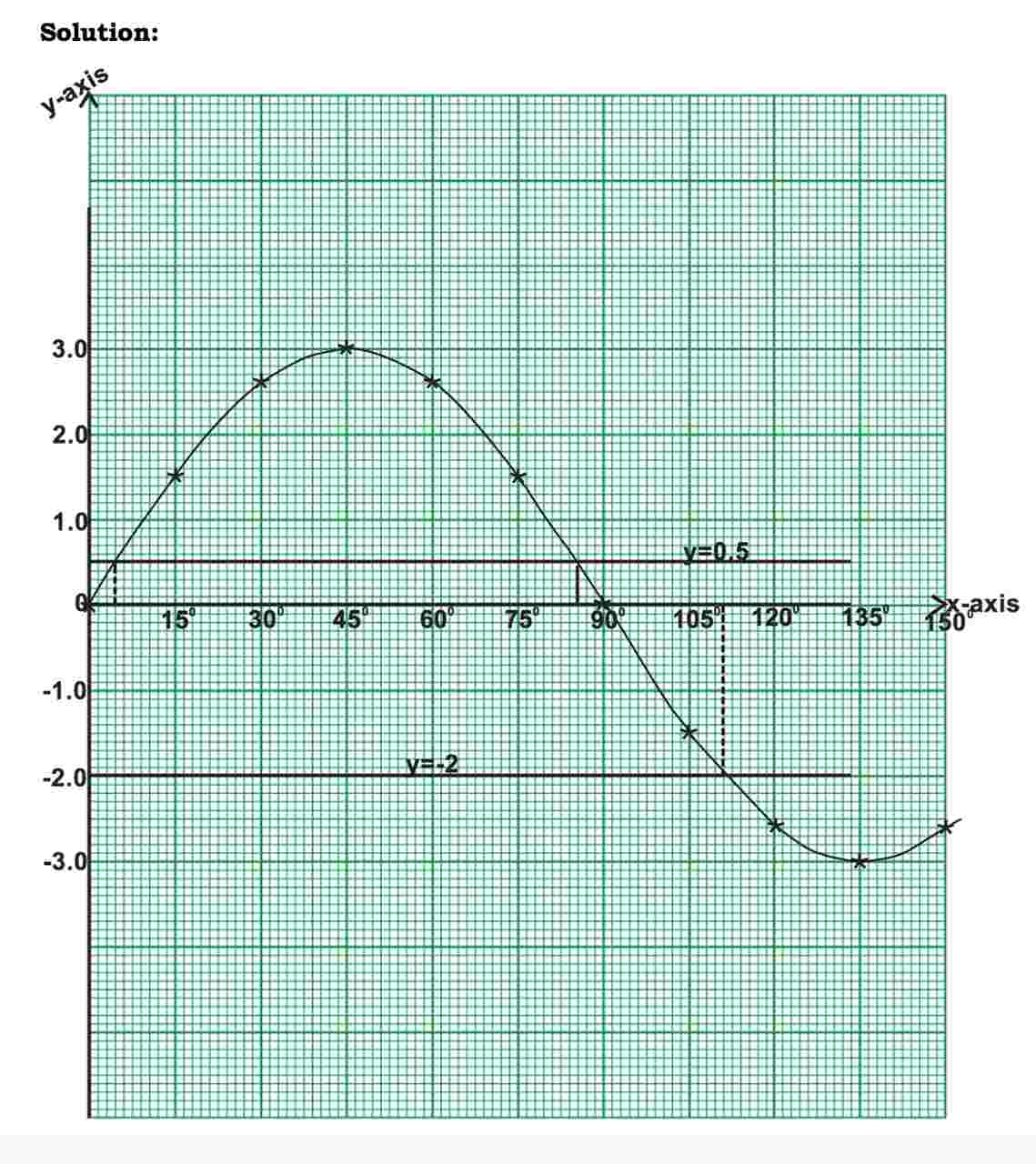
(a) Copy and complete the table of value for the relation y = 3sin2x
x
0ᵒ
15ᵒ
30ᵒ
45ᵒ
60ᵒ
75ᵒ
90ᵒ
105ᵒ
120ᵒ
135ᵒ
150ᵒ
y
0.0
1.5
-2.6
(b) Using a scale of 2 cm to 15ᵒ on the x-axis and 2 cm to 1 unit on the y-axis, draw the graph of y = 3 sin 2x for 0º ≤ x ≤ 150º
(c) Use the graph to find the truth set of
(i) 3 sin 2x + 2 = 0
(ii) \( \frac{3}{2} \scriptsize sin2x \: – \: 0.25 \)
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
Question 7 of 13
7. Question
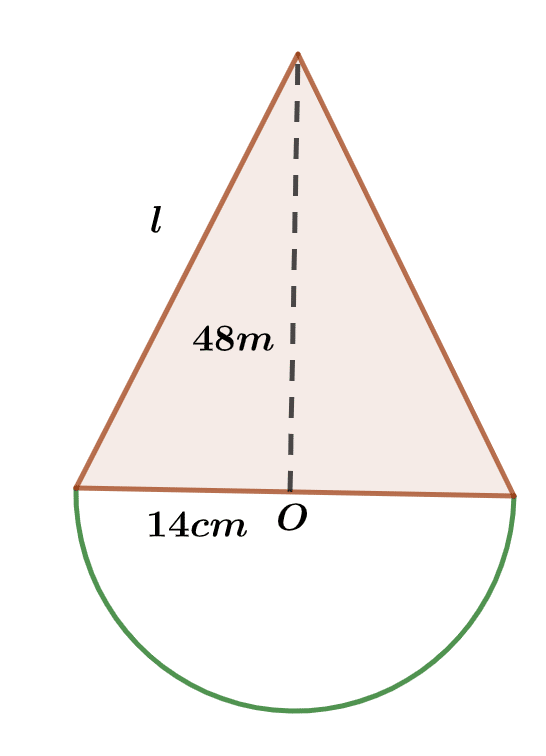
(a) The diagram shows a wooden structure in the form of a cone, mounted on a hemispherical base. The vertical height of the cone is 48m and the base radius is 14m. Calculate, correct to three significant figures, the surface area of the structure.
Take π = \( \frac{22}{7} \)
(b)Five years ago, Musah was twice as old as Sesay’s. If the sum of their ages is 100. Find Sesay’s present age.
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 8 of 13
8. Question
(a) Ms. Maureen spent \( \frac{1}{4}\) of her monthly income at a shopping mall. \( \frac{1}{3}\) at an open market and \( \frac{2}{5}\) of the remaining amount at a Mechanic workshop. If she had ₦225,000.00 left, find:
(i) her monthly income;
(ii) the amount spent at the open market.
(b) The third term of an Arithmetic Progression (A.P) is 4m – 2n. If the ninth term of the progression is 2m – 8n. Find the common difference in terms of m and n
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 9 of 13
9. Question
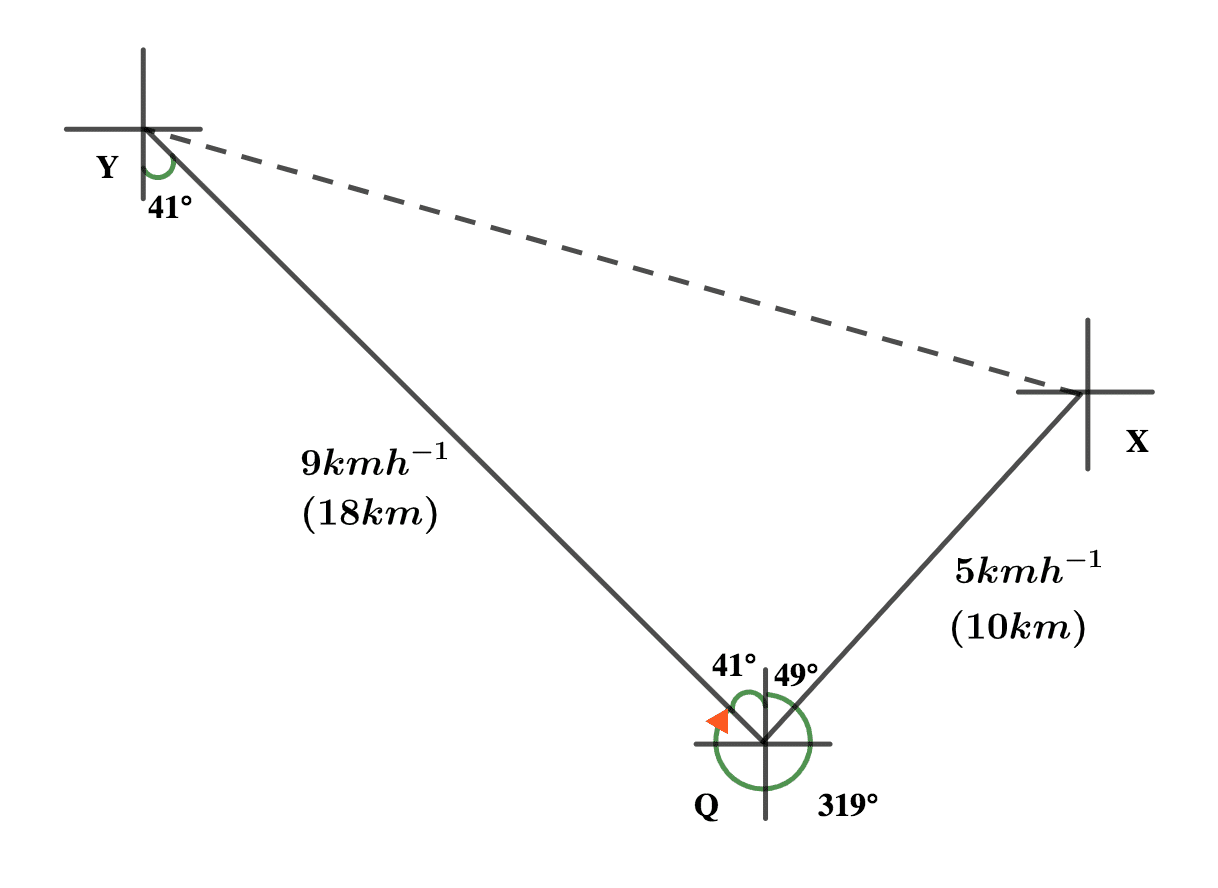
Two cyclists X and Y leave town Q at the same time. Cyclist X travels at the rate of 5 km h on a bearing of 049ᵒ and cyclist Y travels at a rate of 9 km h on a bearing of 319ᵒ.
(a) Illustrate the information on a diagram.
(b) After travelling for two hours, calculate correct to the nearest whole number. The:
(i) Distance between cyclists X and Y
(ii) Bearing of cyclists X and Y.
(c) Find the average speed at which cyclist X will get to Y in 4 hours.
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 10 of 13
10. Question
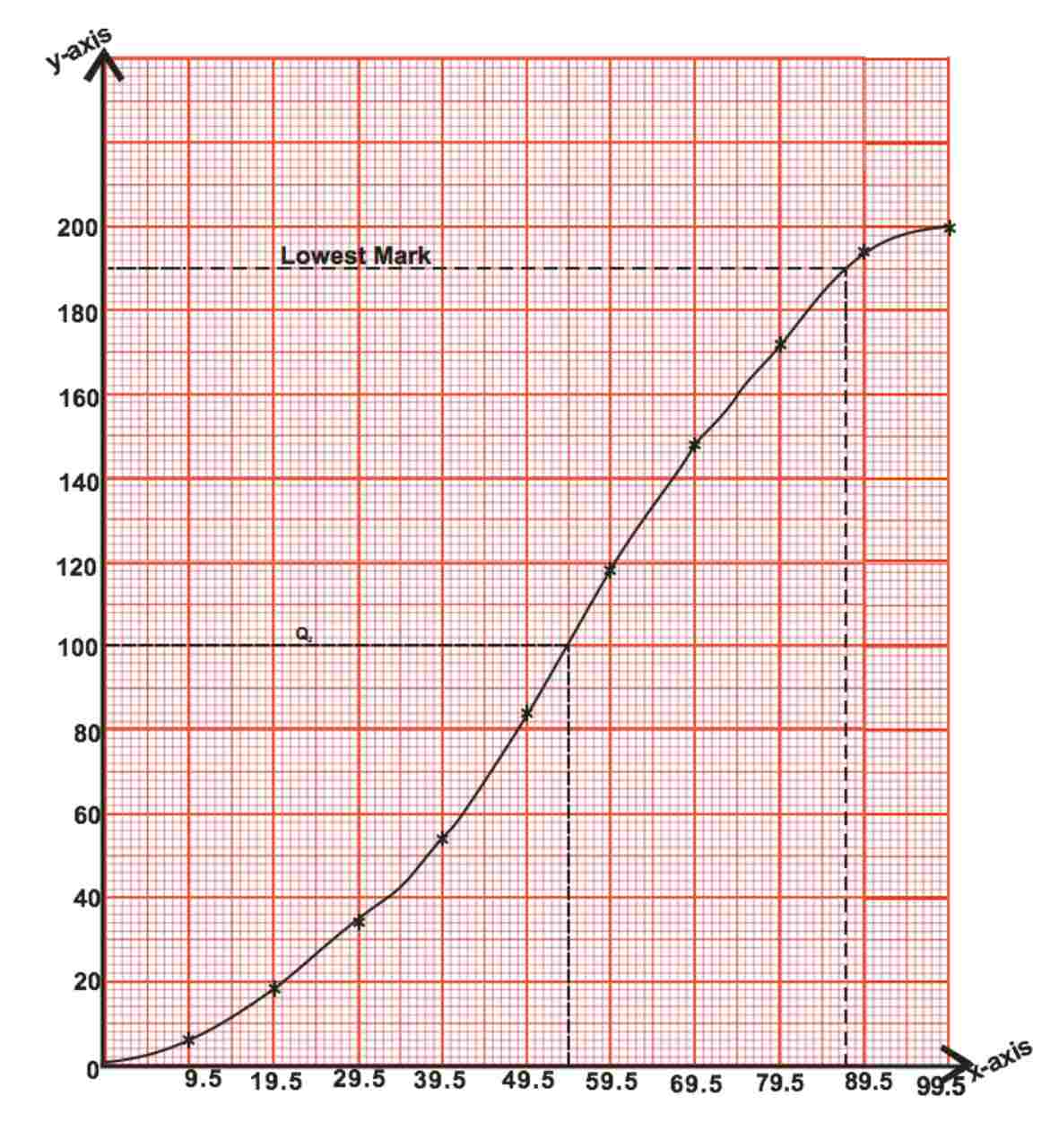
The table shows the distribution of marks obtained by students in an examination

(a) Construct a cumulative frequency table for the distribution
(b) Draw the cumulative frequency curve for the distribution.
(c) Using the curve. Find correct to one decimal place, the:
(i) Median mark.
(ii) Lowest mark for distinction if 5% of the students passed with distinction.
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 11 of 13
11. Question
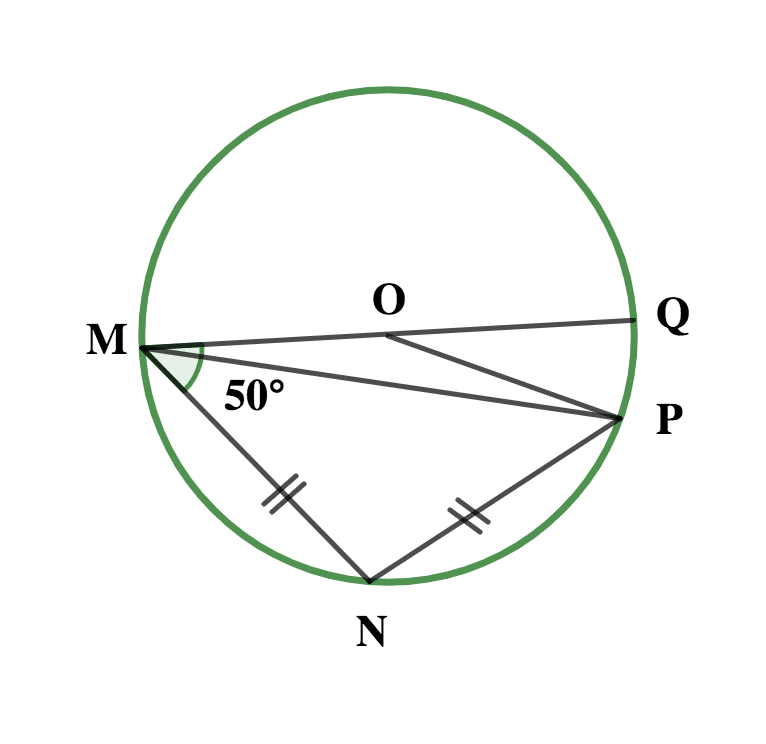
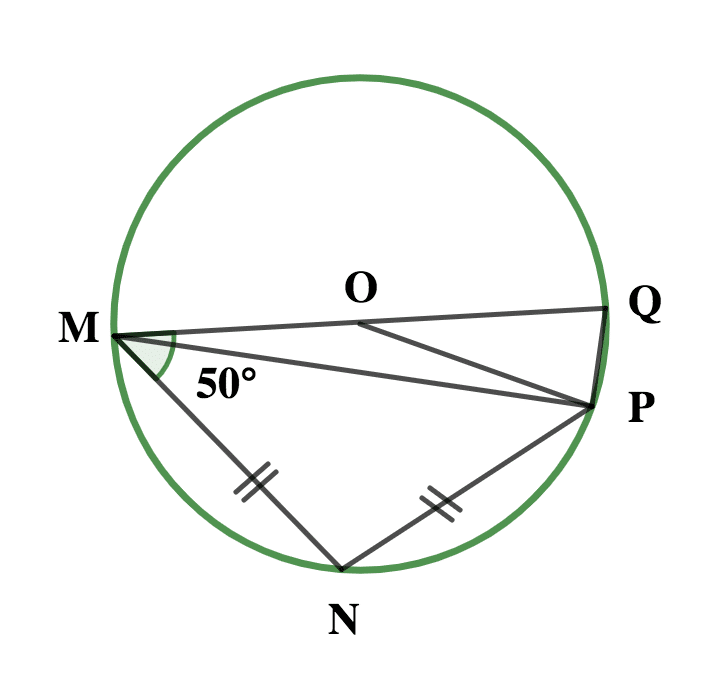
In the diagram, MNPQ is a circle with center O, |MN|=|NP| and ∠OMN=50ᵒ. Find: (i) ∠MNP (ii) ∠POQ
(b)Find the equation of the line which has the same gradient as 8y + 4x = 24 and passes through the point (-8, 12)
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 12 of 13
12. Question
(a)
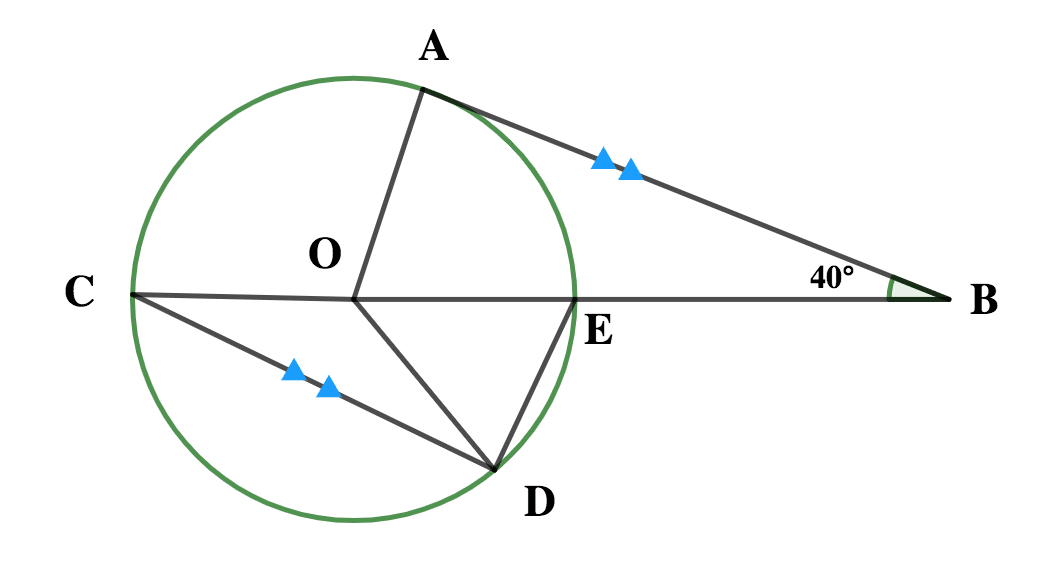
In the diagram, AB is a tangent to the circle with centre O and COB is a straight line. If CD//AB and ∠ABE = 40ᵒ, find ∠ODE
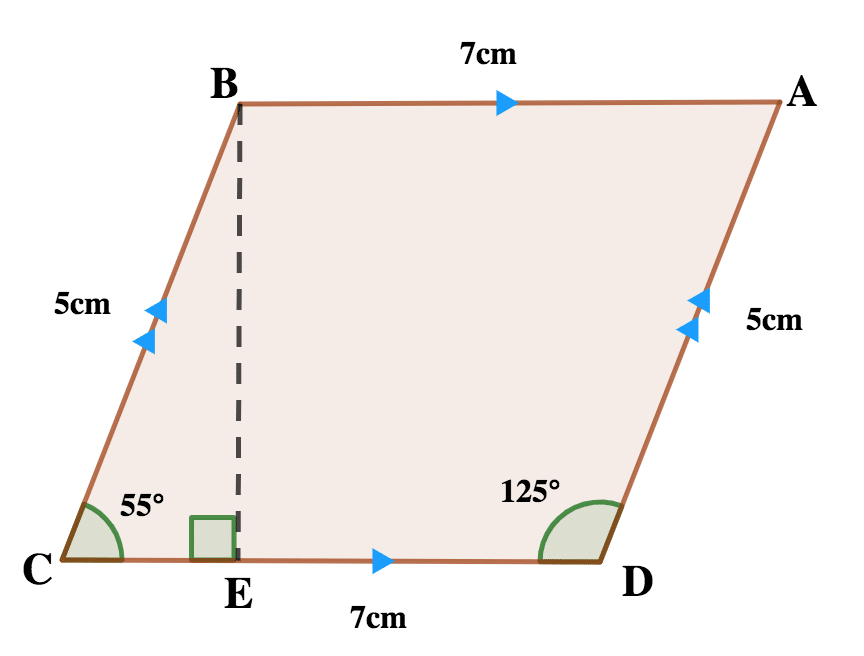
(b) ABCD is parallelogram in which \( \scriptsize \bar{CD} \) = 7cm, \( \scriptsize \bar{AD} \) = 5 cm and ∠ADC = 125ᵒ.
(i) Illustrate the information in a diagram.
(ii) Find, correct to one decimal place, the area of the parallelogram
(c) If \( \scriptsize x = \normalsize \frac{1}{2} \left( \scriptsize1 \: – \: \sqrt{2} \right) \)
Evaluate \( \left( \scriptsize 2x^2 \: – \: 2x \right ) \)
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 13 of 13
13. Question
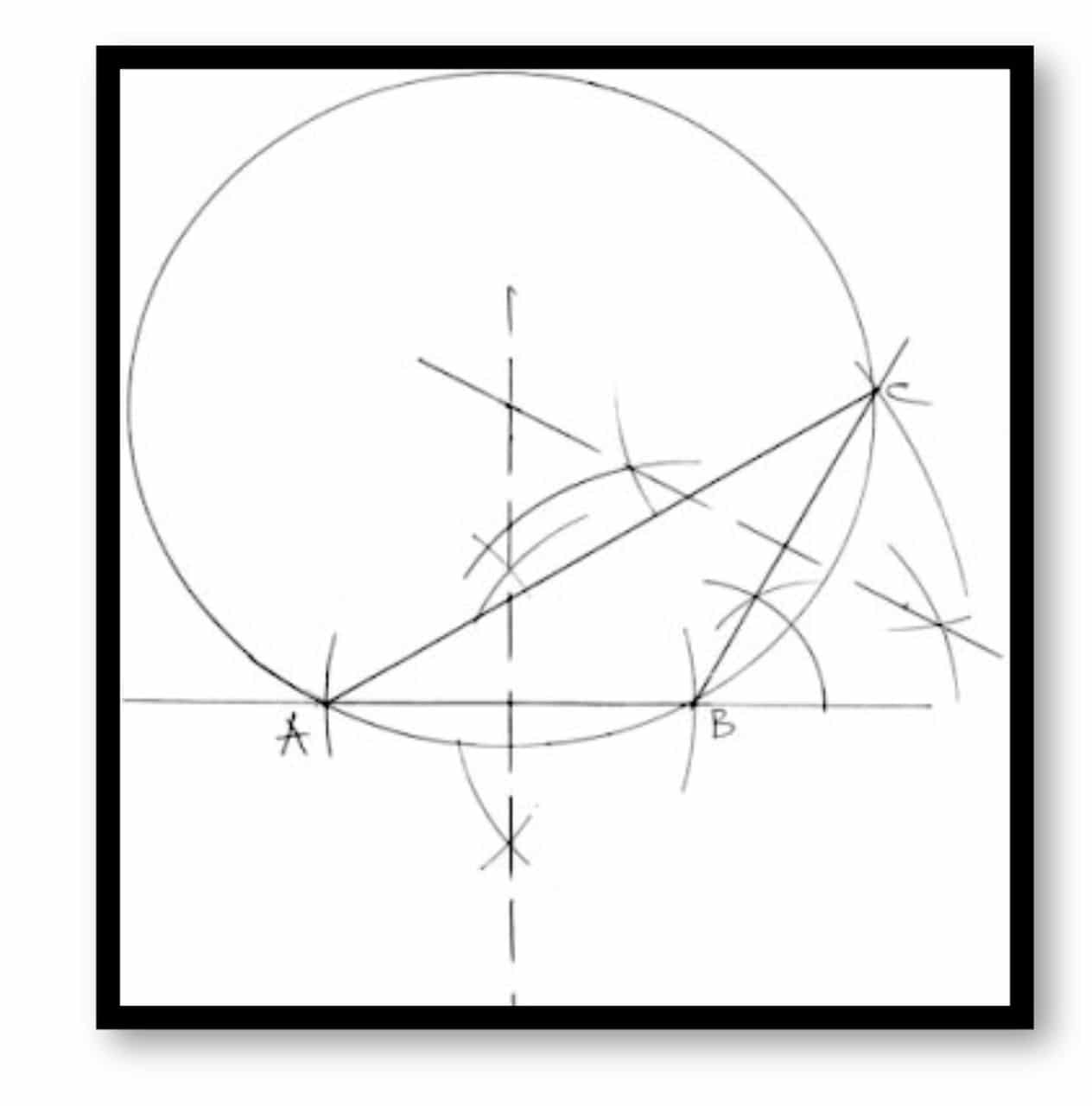
(a) Using a ruler and a pair of compasses only, construct:
(i) ∆ABC with |AB| = 7.5cm. |AC| = 13.5 cm and ∠ABC = 120ᵒ:
(ii) locus l1 of points equidistant from A and B.
(iii) locus l2 of points equidistant from B and C.
(b) Using the method of completing the square, solve \( \scriptsize 4x^2 \: -\: 4\sqrt{3x} \: + \: 3 = 0 \)
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -





Responses