Example 1:
1. a. Express 132four in Binary
Solution
First, convert 132four to Base 10
| Place Value | 2 | 1 | 0 |
| 1 | 3 | 2 |
= 1 × 42 + 3 × 41 + 2 × 40
= 16 + 12 + 2
= 3010
Now convert 3010 to base 2
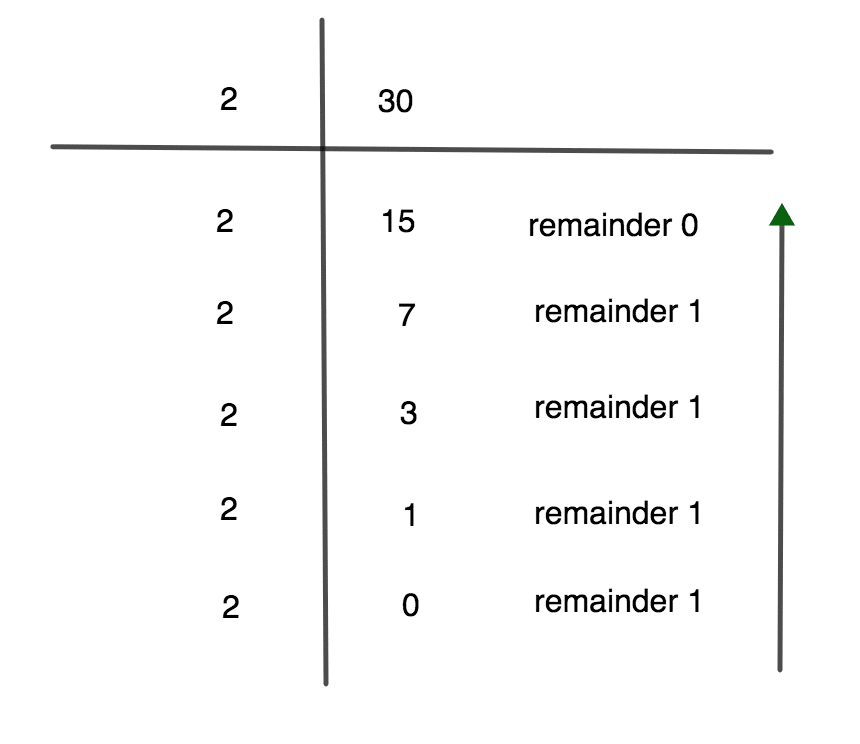
Answer = 111102
1. b. Solve the equation \( \frac{3x \: – \: 2}{8} = \frac{8 \: + \: 5x}{2} \)
Solution
Multiply both sides by 8
\( \normalsize \frac{3x \: – \: 2}{8} \scriptsize \: \times \: 8 = \normalsize \frac{8 \: + \: 5x}{2} \scriptsize \: \times \: 8\) \( \normalsize \frac{3x \: – \: 2}{\not{8}} \scriptsize \: \times \: \not{\!8}^1 = \normalsize \frac{8 \: + \: 5x}{\not{2}} \scriptsize \: \times \: \not{\!8}^4\)(3x – 2) = 4(8 + 5x)
Open the brackets
3x – 2 = 32 + 20x
Collect like terms
3x – 20x = 32 + 2
-17x = 34
Divide both sides by -17
\( \frac{-17x}{-17} = \frac{34}{-17} \) \( \scriptsize x = \normalsize \frac{34}{-17} \)x = -2
Example 2:
2. a. Calculate the size of each angle of a regular pentagon
Solution
Regular pentagon = 5 sides
Each interior angle = \( \frac {n \: – \: 2 \: \times\: 180^o}{n} \)
= \( \frac {5 \: – \: 2 \: \times\: 180^o}{5} \)
= \( \frac {3 \: \times\: 180^o}{5} \)
\( \frac{540^o}{5} \)
= 108º
2. b. The table shows the scores of students in a test.
| Scores | 13 | 14 | 15 | 16 | 18 |
| No of Students | 3 | 5 | 8 | 7 | 12 |
(i) What is the modal score?
(ii) How many students took part in the test?
(iii) Find the median score
Solution
(i) Modal score = highest frequency = 18
(ii) Number of students = 3 + 5 + 8 + 7 + 12 = 35 students
(iii) Median score (middle score)
First list out the scores
13, 13, 13, 14, 14, 14, 14, 14, 15, 15, 15, 15, 15, 15, 15, 15, 16, 16, 16, 16, 16, 16, 16, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18
Total frequency = 35
median = \( \frac{n \: + \: 1}{2} \)
= \( \frac{35 \: + \: 1}{2} \)
= \( \frac{36}{2} \)
= 18
The median score is the 18th frequency or score which is 16
13, 13, 13, 14, 14, 14, 14, 14, 15, 15, 15, 15, 15, 15, 15, 15, 16, 16, 16, 16, 16, 16, 16, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18
Example 3:
3. Find the largest angle in the figure below
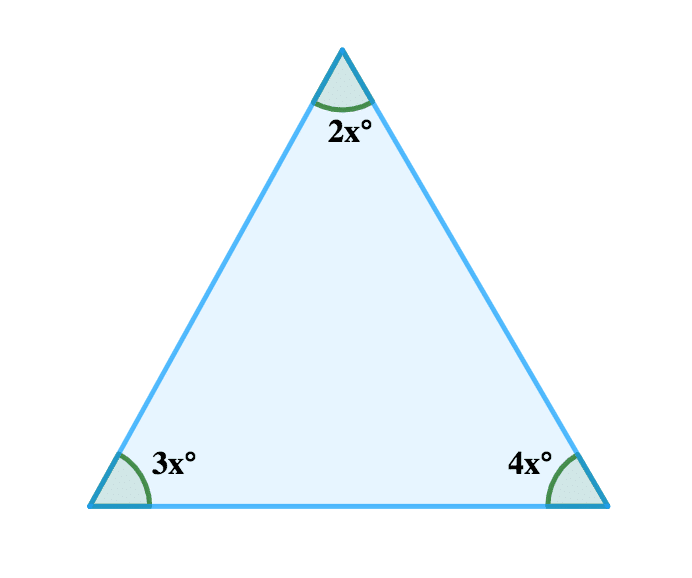
Solution
Sum of angles in a triangle = 180º
∴ 2xº + 3xº + 4xº = 180º
9xº = 180º
Divide both sides by 9
\( \frac{9x}{9} = \frac{180}{9} \)x = 20º
From the triangle the biggest angle has to be 4x
Substitute x = 20º into 4x
4x = 4 × 20º
= 80º
Example 4:
4. The height of an equilateral triangle is 15 cm and its perimeter is 36 cm. Find the area of the triangle.
Solution
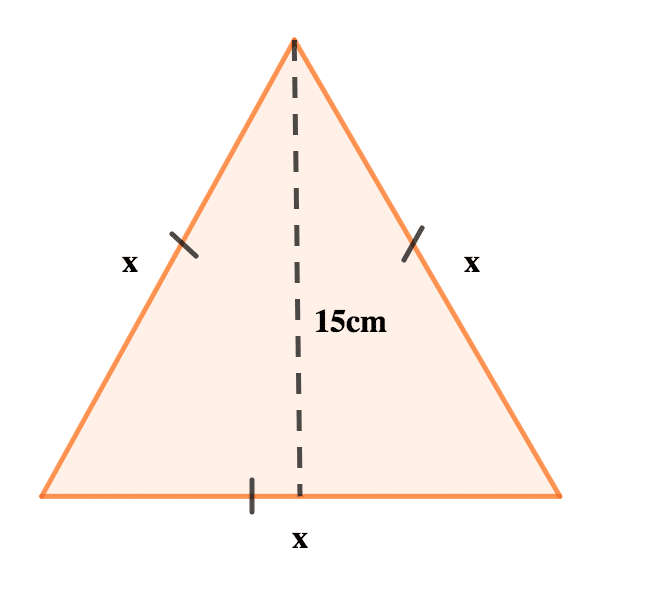
Perimeter of triangle = x + x + x
Permieter = 36 cm
∴ 36 = x + x + x
36 = 3x
3x = 36
Divide both sides by 3
\( \frac{3x}{3} = \frac{36}{3} \)
x = 12
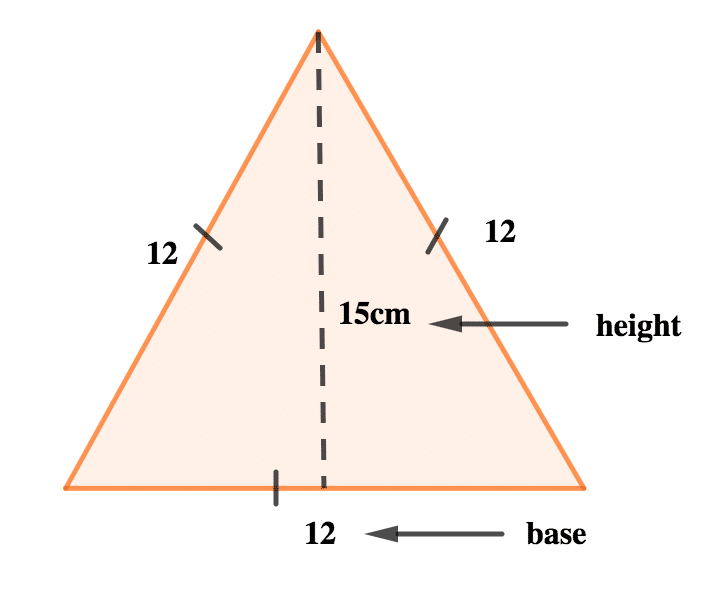
Area of the triangle = \( \frac{1}{2} \scriptsize \: \times \: base \: \times \: height \)
= \( \frac{1}{2} \scriptsize \: \times \: 12 \: \times \: 15 \)= 6 × 15
= 90 cm2
Example 5:
5. Calculate /DC/ using the similar shapes given below
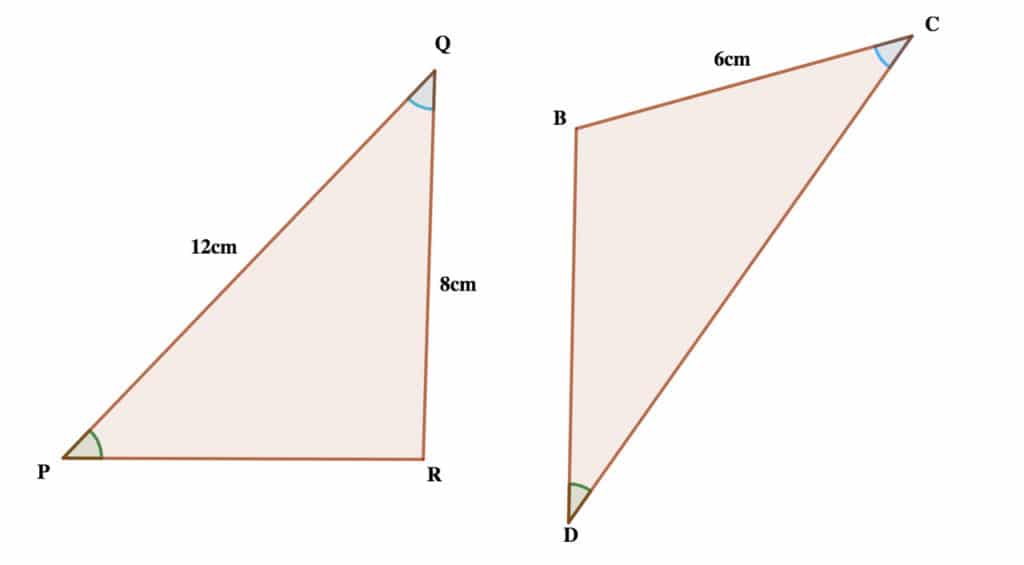
Solution
The two triangles are similar
∴ \( \frac{|PQ|}{|QR|} = \frac{|DC|}{|BC|} \)
= \( \frac{12}{8} = \frac{|DC|}{6} \)
Cross multiply
8 × DC = 12 × 6
8DC = 72
Divide both sides by 8
\( \frac{8DC}{8} = \frac{72}{8} \)
DC = 9 cm
Example 6:
6. What is the average rainfall in mm2 from the bar chart below?
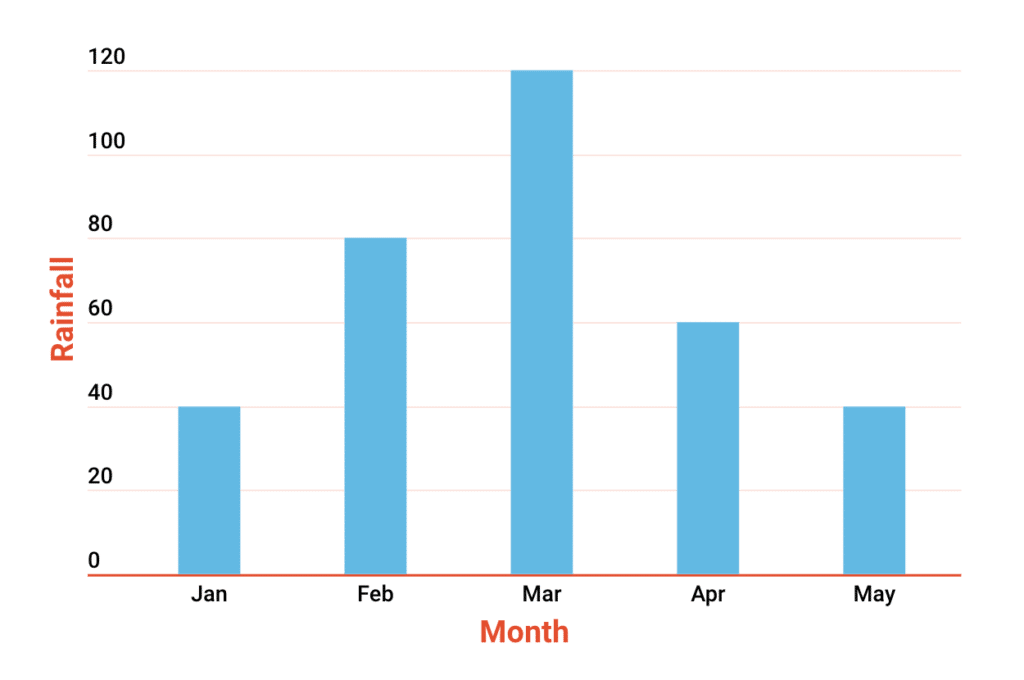
Solution
| Jan | 40 |
| Feb | 80 |
| Mar | 120 |
| Apr | 60 |
| May | 40 |
Average Rainfall
= \( \frac{40+80+120+60+40}{5} \)
= \( \frac{340}{5} \)
= 68 mm2
Example 7:
7. Find the missing angles l, m and n in that order from the diagram below
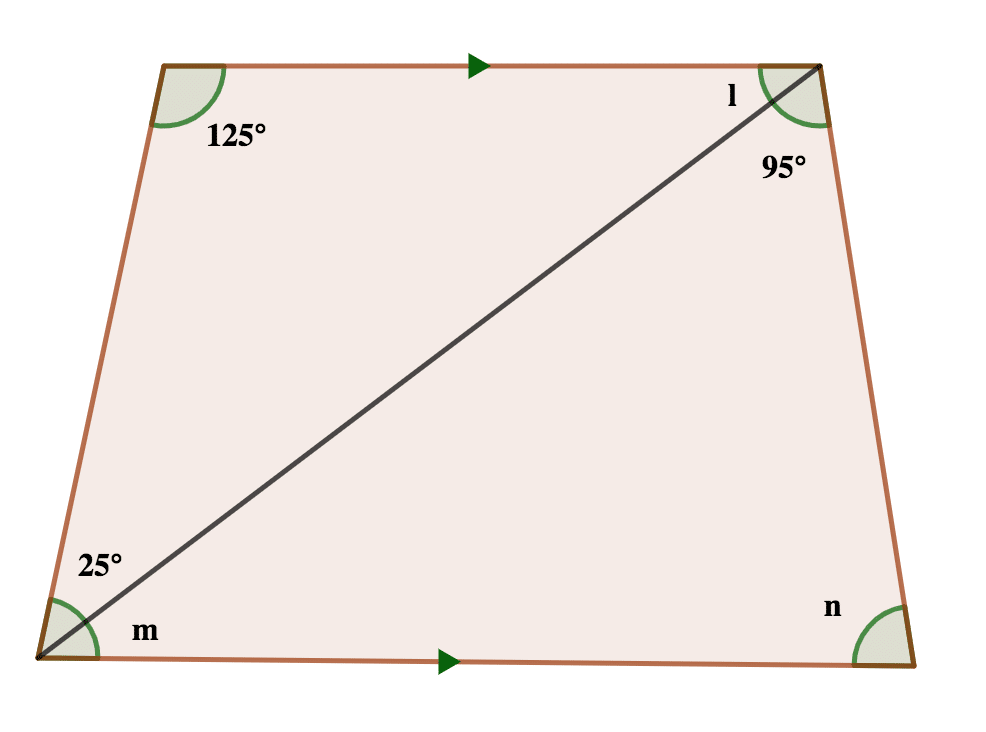
Solution
The shape is a trapezoid.
Opposite angles of a trapezoid are supplementary. Supplementary angles of a trapezoid is defined as the sum of two opposite angles is 180
∴ n + 125 = 180
n = 180 – 125 = 55º
Also,
(25 + m) + (95 + l) = 180
But m = l (alternate angles)
so let’s say l and m = x
∴ (25 + x) + (95 + x) = 180
25 + x + 95 + x = 180
25 + 95 + x + x = 180
120 + 2x = 180
2x = 180 – 120
2x = 60
x = \( \frac{60}{2} \)
x = 30
∴ l and m = 30º
Answer: l, m and n = 30º, 30º and 55º
Example 8:
8. Simplify \( \frac{x^2 – 6x + 9}{x^2 – 9} \)
Solution
First step: Factorise the numerator
\( \scriptsize x^2 \: – \: 6x \: + \: 9 \) =\( \scriptsize x^2 \: – \: 3x \: – \: 3x \: + \: 9 \)= \( \scriptsize x(x \: – \: 3) \: – \: 3(x \: – \: 3) \)
= (x – 3)(x – 3)
Second step: Factorise the denominator
x2 – 9
= x2 – 32
= (x – 3)(x + 3) (Difference of two squares)
∴ \( \frac{x^2 – 6x + 9}{x^2 – 9} = \frac{(x – 3)(x – 3)}{(x – 3)(x + 3)}\)= \( \frac{(x – 3)}{(x + 3)}\)
Example 9:
9. In the diagram below, ABCD is a kite and ADEF is a rhombus. If BC = 4 cm and CD = 7 cm, find the perimeter of ABCDEF (Not drawn to scale)
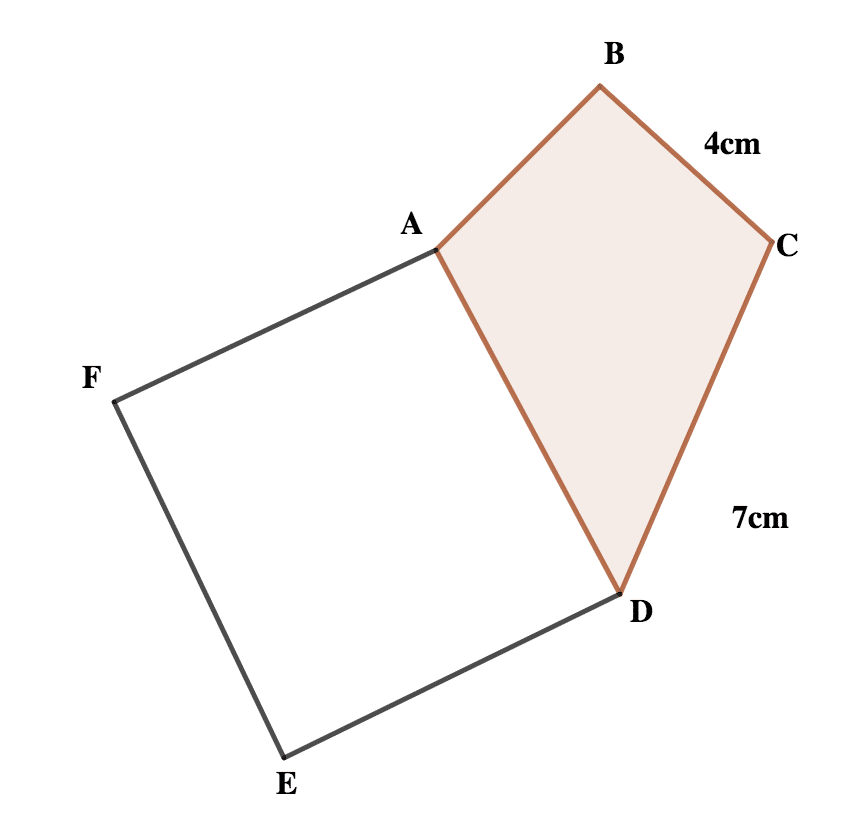
Solution
We can redraw the diagram as shown below.
A kite has 2 pairs of adjacent equal sides
A rhombus has all sides equal
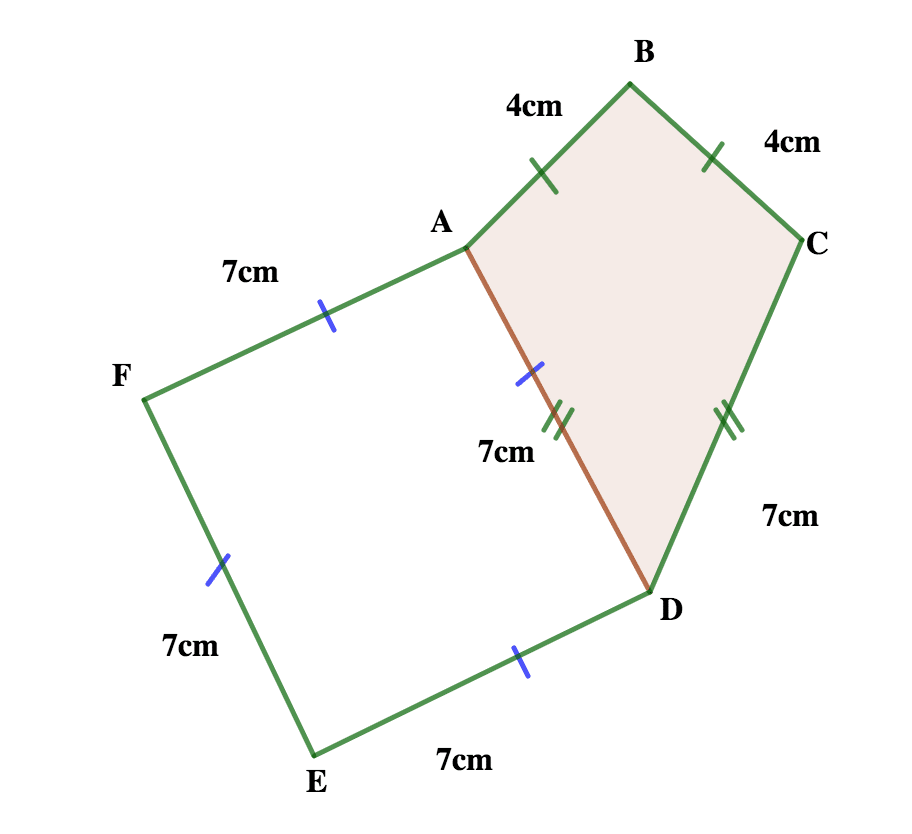
A perimeter of a shape is the length of its boundary or the total length around the shape
= 7 + 7 + 7 + 4 + 4 + 7
= 36 cm
Note: Perimeter is the total length around the shape so we ignore the side in the middle (7 cm)
Example 10:
10. An exercise book and two pens cost ₦90.00. If the difference between the cost of an exercise book and a pen is ₦45.00, determine the cost of a pen.
Solution
Let the cost of an exercise book = x
the cost of a pen = y
From the question
An exercise book and two pens cost ₦90.00
x + 2y = 90 ……………..(1)
The difference between the cost of an exercise book and a pen is ₦45.00
x – y = 45 …………………(2)
Subtract equation 2 from 1
x + 2y = 90
x – y = 45
2y – (-y) = 90 – 45
2y + y = 45
3y = 45
y = \( \frac{45}{3} \)
y = ₦15
Practice JSCE Mathematics Past Questions:
Prepare with our past questions from 2023 – 2015 and get access to clear diagrams, detailed explanations and instant results/feedback.









Responses
I need real practice