Calculating Distance Along Great Circle

Note that the shortest distance between two points on the surface of the earth lies on the arc length of a great circle connecting the two points. Let the arc length be \( \scriptsize \overline{AB} \), then

\( \scriptsize \overline {AB} = \normalsize \frac{θ°}{360°} \scriptsize \times 2 \pi R\)

Where  θ° = angular difference

  R = radius of the earth = 6,400Km

  π = \( \frac{22}{7} \)

Example 1

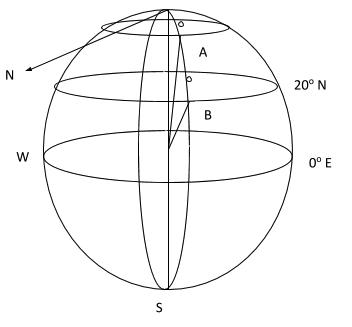
A and B are two places on the earth’s surface on the same meridian. B has a Latitude of 20° N and A is a point north of B such that the distance AB measured along the meridian is 800Km.
Calculate the Latitude of A correct to the nearest degree,
(Take π = \( \frac{22}{7} \) and R = 6,400Km.)

Solution:

\( \scriptsize \overline {AB} = \normalsize \frac{θ°}{360°} \scriptsize \times 2 \pi R\)

\( \scriptsize \overline{AB} = 800 \)

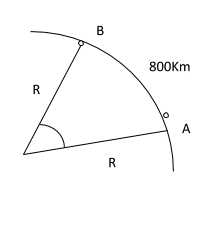
800 =  \(\frac{θ}{360} \: \times \: \scriptsize 2 \: \times \: \normalsize \frac{22}{7} \scriptsize \: \times \: 6400 \)

θ = \( \frac{800 \: \times \: 360\: \times \: 7}{44 \: \times \: 6400} \)

= \( \frac{45 \: \times \: 7}{44} \)

θ = 7.1590

θ = 7° (nearest degrees)

Since the two points are in the same direction

θ = Latitude A – Latitude B

i.e. 7 = Latitude A – 20

Therefore, Latitude A = 7 + 20

i.e. Latitude A = 27° N

Example 2

(a) An aeroplane flies from city A (0°, 152° E) to city B (0°, 171° W), find the shortest distance travelled to reach city B

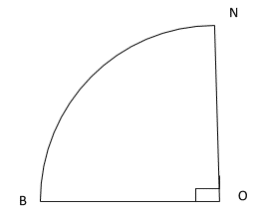
(b) How far is city B from the North Pole? (Take π = \( \frac{22}{7} \) and R = 6,400Km.)

Solution:

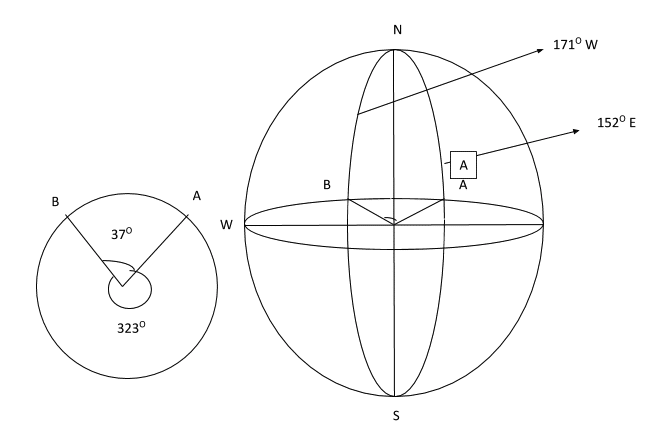
The angular difference between points A and B is 323° which gives the major segment – it does not give the shortest distance, rather the minor segment of 37° gives the shortest distance.

Recall that from the equator 0° to the North Pole, the angular difference is 90°.

Therefore, \( \scriptsize \bar{BN} = \normalsize \frac{θ}{360} \: \times \: \scriptsize 2 \: \times \: \normalsize \frac{22}{7} \scriptsize \: \times \: 6400 \)

= \( \scriptsize \bar{BN} = \normalsize \frac{90}{360} \: \times \: \scriptsize 2 \: \times \: \normalsize \frac{22}{7} \scriptsize \: \times \: 6400 \)

= 10,057.1429

\( \scriptsize \bar{BN} = 10,057Km \)