WAEC: MATHEMATICS
Quizzes
-
2021 Mathematics WAEC Objective Past Questions
-
2021 Mathematics WAEC Essay Past Questions
-
2020 Mathematics WAEC Objective Past Questions
-
2020 Mathematics WAEC Theory Past Questions
-
2019 Mathematics WAEC Objective Past Questions
-
2019 Mathematics WAEC Theory Past Questions
-
2018 Mathematics WAEC Objective Past Questions
-
2018 Mathematics WAEC Theory Past Questions
-
2017 Mathematics WAEC Objective Past Questions
-
2017 Mathematics WAEC Theory Past Questions
-
2016 Mathematics WAEC Objective Past Questions
-
2016 Mathematics WAEC Theory Past Questions
-
2015 Mathematics WAEC Objective Past Questions
-
2015 Mathematics WAEC Theory Past Questions
-
2014 Mathematics WAEC Objective Past Questions
-
2014 Mathematics WAEC Theory Past Questions
Quiz Summary
0 of 13 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 13 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 13
1. Question
(a) Without using tables or calculator, simplify :
\(\frac{0.6 \: \times \: 32 \: \times \: 0.004}{1.2 \: \times \: 0.008 \: \times \: 0.16}\)
leaving the answer in standard form (scientific notation).
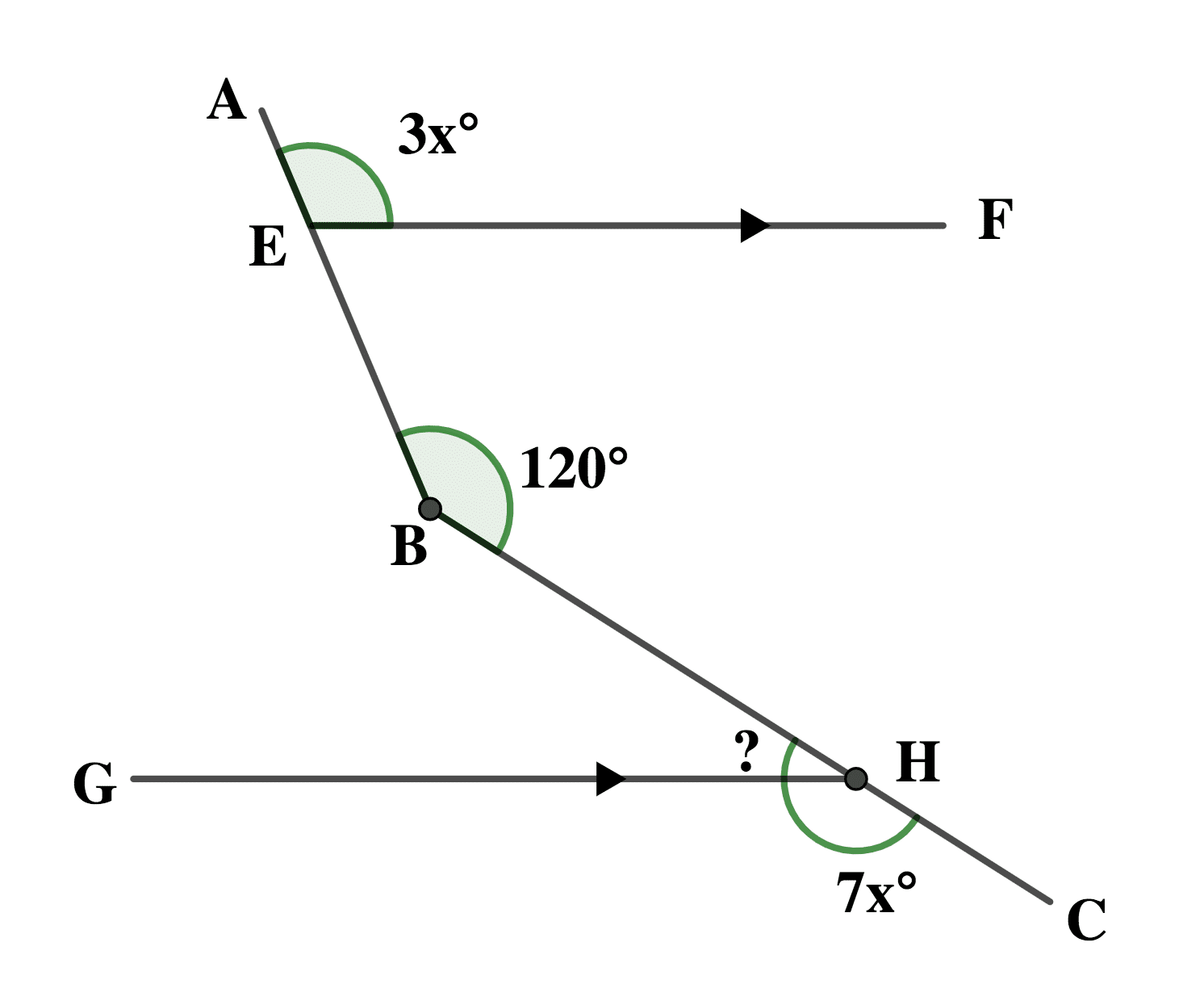
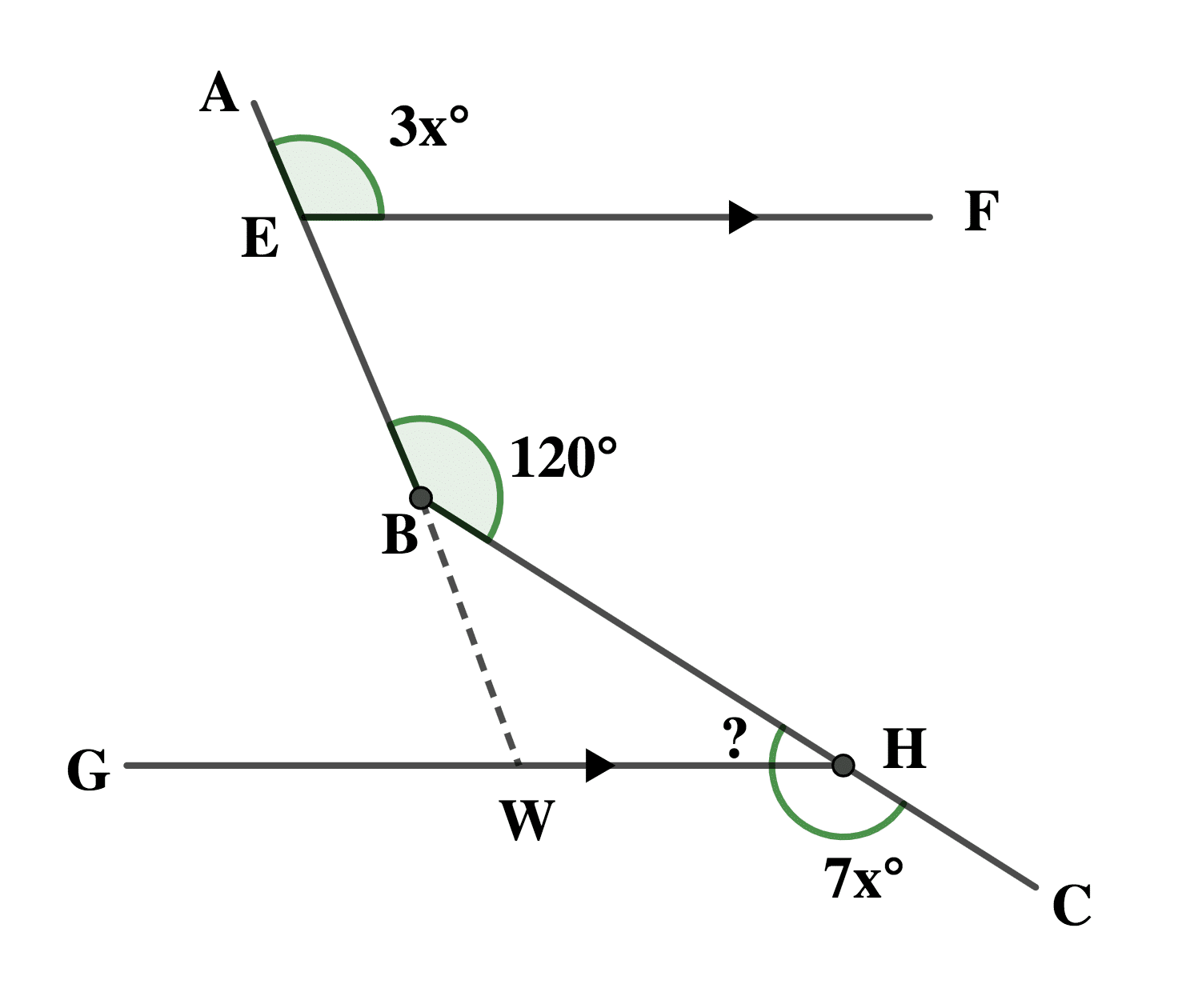
(b) In the diagram, \(\scriptsize\overline{EF}\) is parallel to \(\scriptsize\overline{GH}\).
If < AEF = 3x°,< ABC = 120° and < CHG = 7x°, find the value of < GHB.
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 2 of 13
2. Question
(a) Simplify : 3√75 – √12 + √108, leaving the answer in surd form (radicals).
(b) If 124n = 232five, find n.
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 3 of 13
3. Question
(a) Solve the simultaneous equation:
\( \frac{1}{x} \: + \: \frac{1}{y} \scriptsize = 5 \)
\( \frac{1}{y} \: – \: \frac{1}{x} \scriptsize = 1 \)
(b) A man drives from Ibadan to Oyo, a distance of 48km in 45 minutes. If he drives at 72 km/h where the surface is good and 48 km/h where it is bad, find the number of kilometers of good surface.
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 4 of 13
4. Question
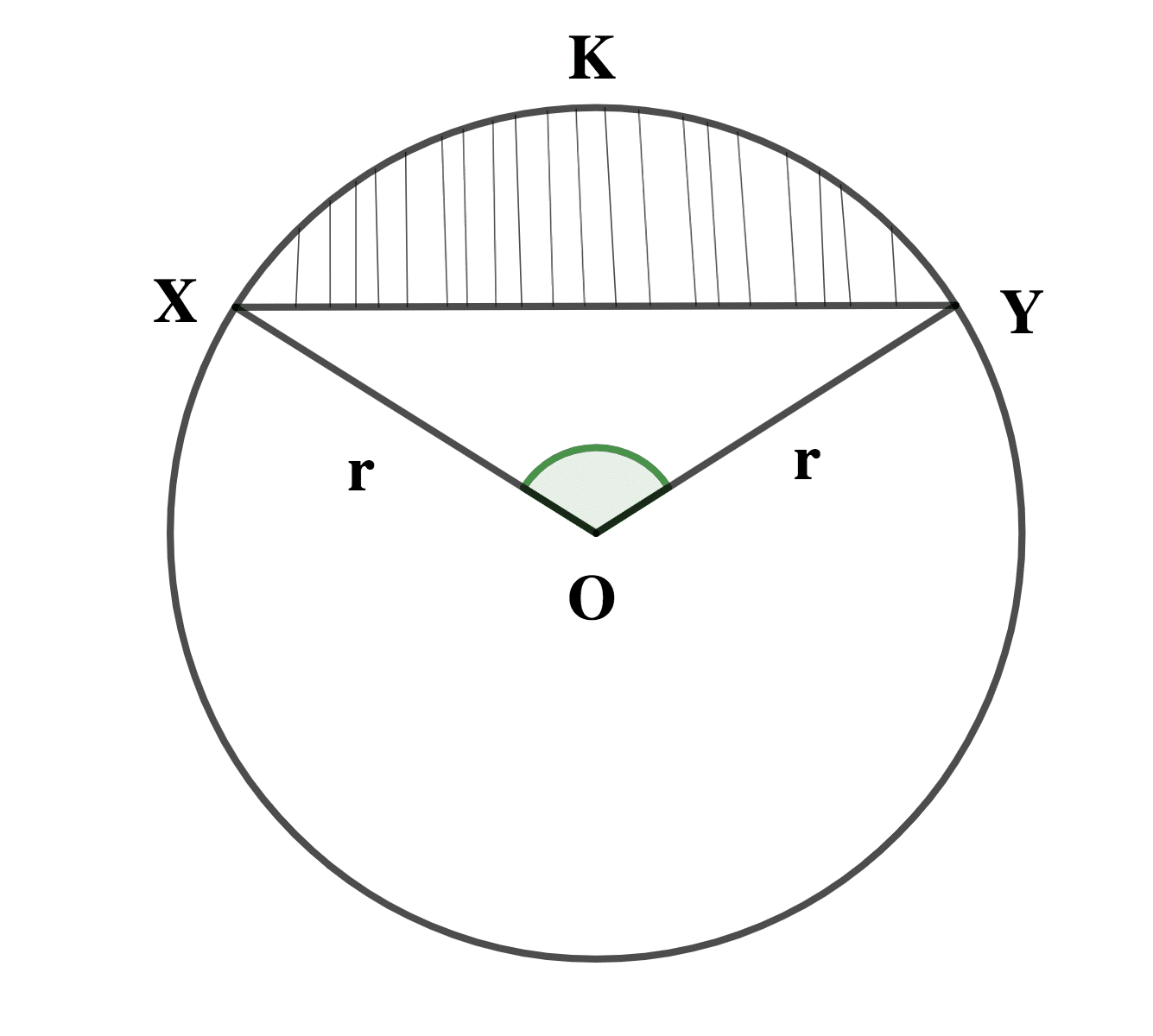
(a) In the diagram, O is the centre of the circle radius r cm and < XOY = 90°. If the area of the shaded part is 504cm2, calculate the value of r. [Take π=22/7].
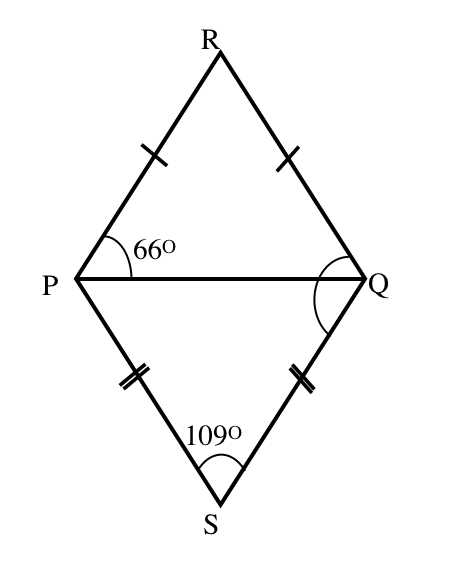
(b) Two isosceles triangles PQR and PQS are drawn on opposite sides of a common base PQ. If <PQR = 66° and <PSQ = 109°, calculate the value of <RQS.
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 5 of 13
5. Question
A building contractor tendered for two independent contracts, X and Y. The probabilities that he will win contract X is 0.5 and not win contract Y is 0.3, What is the probability that he will win :
(a) both contracts ;
(b) exactly one of the contracts ;
(c) neither of the contracts?
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 6 of 13
6. Question
(a) If \(\frac{3}{2p\: – \: \frac{1}{2}} = \frac{\frac{1}{3}}{\frac{1}{4}p \: + \: 1}\)
find p(b) A television set was marked for sale at GH¢ 760.00 in order to make a profit of 20%. The television set was actually sold at a discount of 5%. Calculate, correct to 2 significant figures, the actual percentage profit.
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 7 of 13
7. Question
(a) Copy and complete the table of values for the relation
y = 2 sinx + 1
x 0° 30° 60° 90° 120° 150° 180° 210° 240° 270° y 1.0 2.7 0.0 -0.7 (b) Using scales of 2cm to 300 on the x-axis and 2cm to 1 unit on the y-axis, draw the graph of
\( \scriptsize y = 2 sinx \: + \: 1 \: for \: 100 \leq x \leq 270^o \)
7c. Use the graph to find the values of x for which \( \scriptsize Sinx = \normalsize \frac{1}{4} \)
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 8 of 13
8. Question
(a) Copy and complete the following table for multiplication modulo 11.
⊗ 1 5 9 10 1 1 5 9 10 5 5 9 9 10 10 Use the table to:
i. Evaluate (9 ⊗ 5) ⊗ (10 ⊗ 10);
ii. Find the truth set of
(a) 10 ⊗ m = 2
(b) n ⊗ n = 4.
b. When a fraction is reduced to its lowest term, it is equal to \( \frac{3}{4} \) . The numerator of the fraction when doubled would be 34 greater than the denominator. Find the fraction.
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 9 of 13
9. Question
(a)
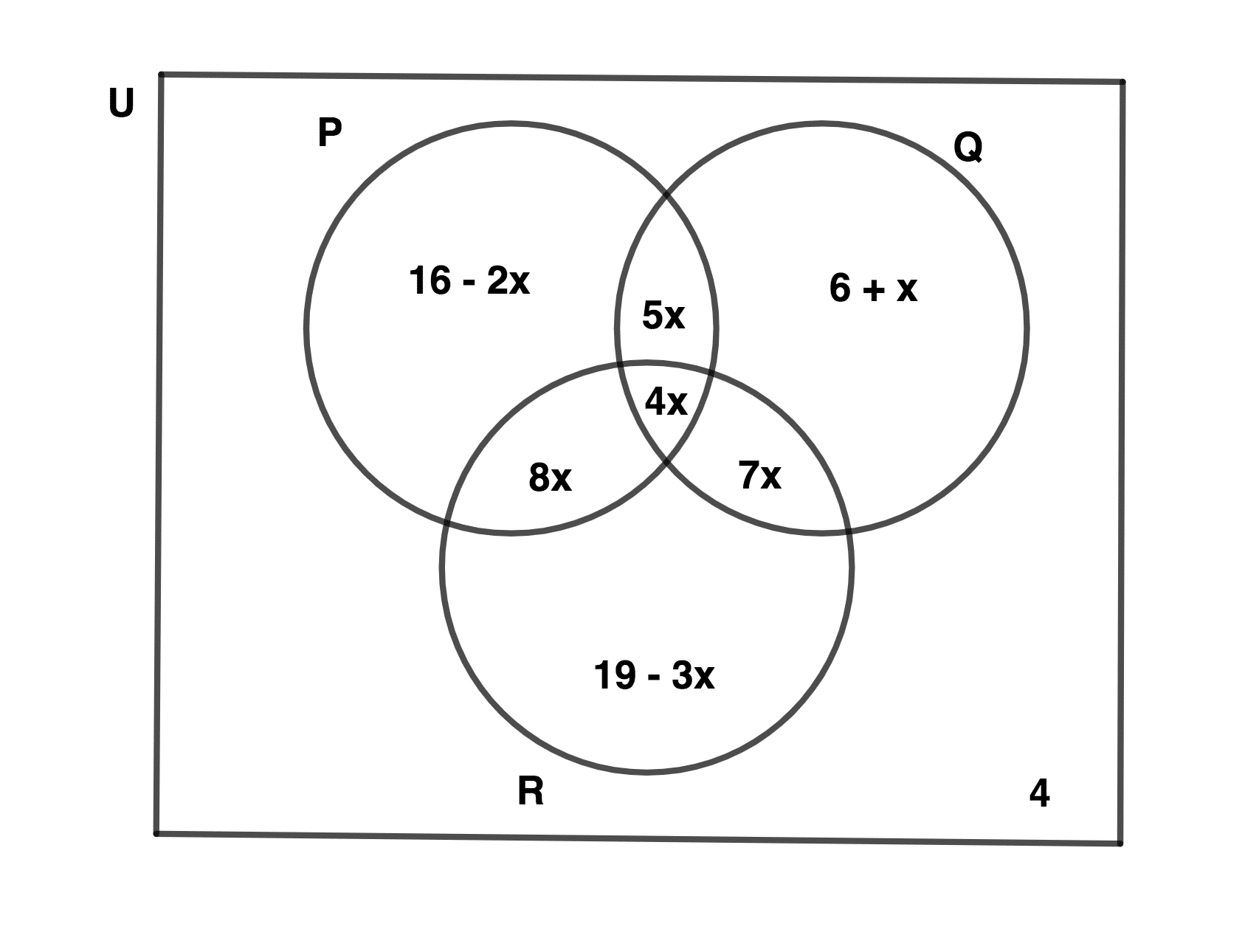
In the Venn diagram, P, Q and R are subsets of the universal set U. If n(U) = 125, find:
i. the value of x
ii. \( \scriptsize n( P \cup Q \cap R’) \)
(b)
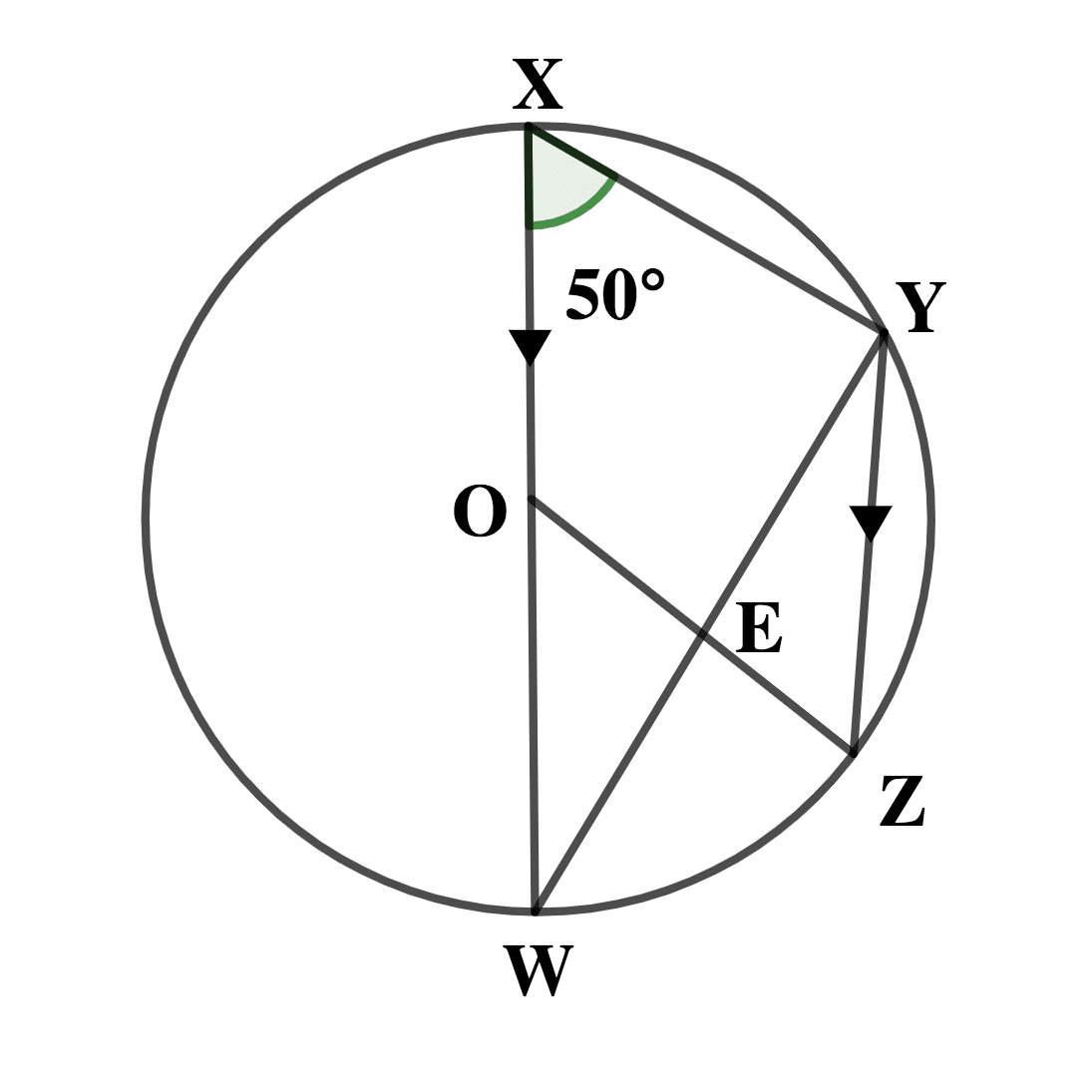
In the diagram, O is the centre of the circle. If WX is parallel to YZ and <WXY = 500, find the value of :
i. <WYZ
ii. <YEZ
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 10 of 13
10. Question
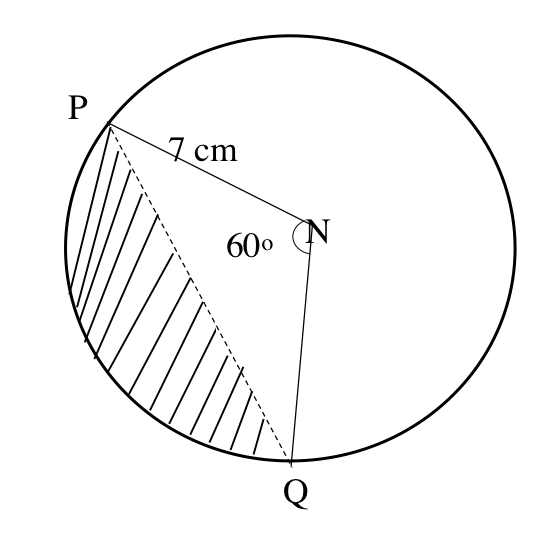
(a) Solve (x – 2)(x – 3) = 12
(b)
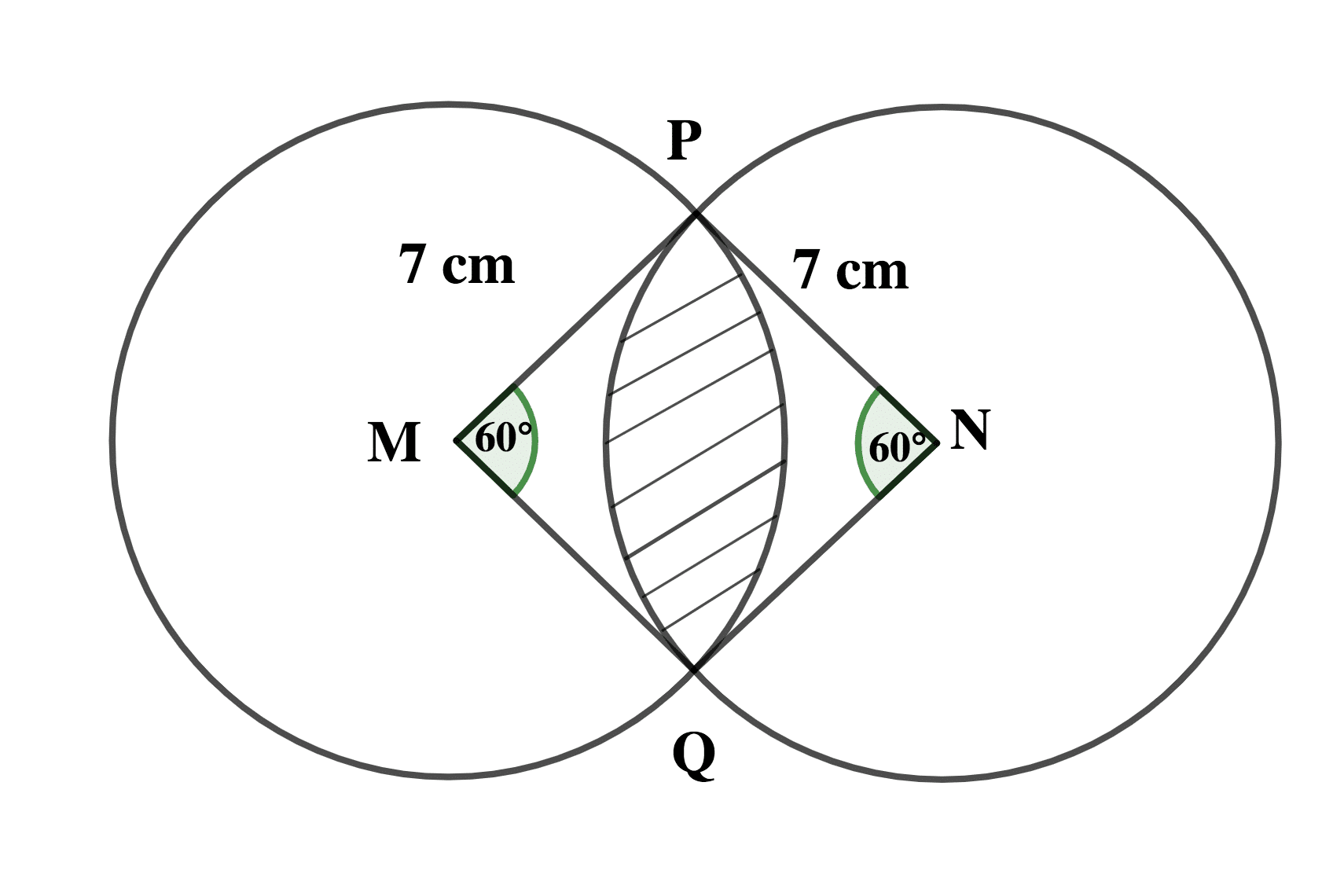
In the diagram, M and N are the centres of two circles of equal radii 7cm. The circles intercept at P and Q. If < PMQ = < PNQ = 60°, calculate, correct to the nearest whole number, the area of the shaded portion.
\( \left [ \scriptsize Take \: \pi \: = \normalsize \frac{22}{7} \right ] \)
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 11 of 13
11. Question
(a)
Scores 1 2 3 4 5 6 Frequency 2 5 13 11 9 10 The table shows the distribution of outcomes when a die is thrown 50 times. Calculate the
i. Mean deviation of the distribution
ii. Probability that a score selected at random is at least a 4.
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 12 of 13
12. Question
(a) Given that \( \scriptsize 5cos(x \: + \: 8.5)^o \: – \: 1 = 0,\: 0^o \leq x \leq 90^o \)
calculate, correct to the nearest degree, the value of x.
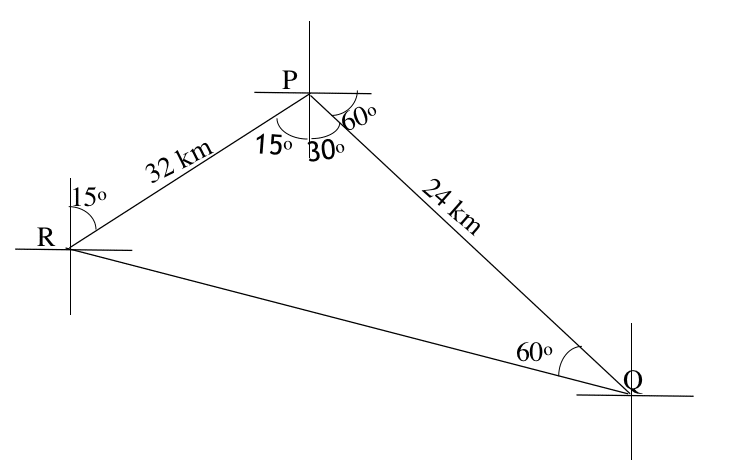
(b) The bearing of Q from P is 0150° and the bearing of P from R is 015°. If Q and R are 24km and 32km respectively from P
(i) represent this information in a diagram;
(ii) calculate the distance between Q and R, correct to two decimal places
(iii) find the bearing of R from Q, correct to the nearest degree.
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -
-
Question 13 of 13
13. Question
(a) Two functions, f and g, are defined by
\( \scriptsize f : x \rightarrow 2x^2 \: – \: 1 \: and \: g: x \rightarrow 3x \: + \: 2 \)
where x is a real number.
(i) If f(x – 1) – 7 = 0, find the values of x
(ii) Evaluate \( \frac{f \left( -\frac{1}{2} \right).g(3)}{f(4) \: – \: g(5)} \)
(b) An operation, \( \scriptsize (\ast) \) is defined on the set R, of real numbers, by \( \scriptsize m(\ast)n \)= \( \frac{-n}{m^2 \: + \: 1} \)
where \( \scriptsize m, n \epsilon R \)
If \( \scriptsize -3, -10 \epsilon R \) Show whether or not \( \scriptsize (\ast) \) is commutative
-
This response will be reviewed and graded after submission.
Grading can be reviewed and adjusted.Grading can be reviewed and adjusted. -




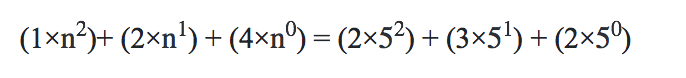
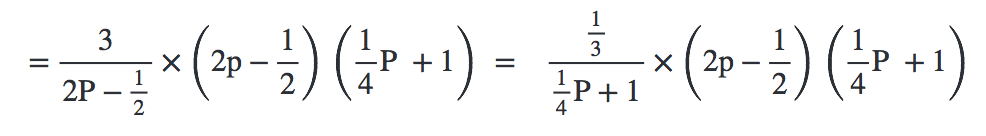

Responses