Back to Course

WAEC: MATHEMATICS

0% Complete
0/0 Steps

Quizzes




  • Kofa Study
Quiz 2 of 16

2021 Mathematics WAEC Essay Past Questions

WAEC: MATHEMATICS 2021 Mathematics WAEC Essay Past Questions

Responses

Your email address will not be published. Required fields are marked *

2021 WAEC Mathematics Essay Question 1a

Question

Mr Sarfo borrowed $25,000.00 from AFIAK Financial Services at 21% simple interest per annum for 3 years. If he was able to pay back the loan in 2 years at equal yearly instalments, how much did he pay each year?

Solution

S.I = \( \frac{P\: \times \: R \: \times \: T}{100} \)

S.I = \( \frac{2500\: \times \: 3 \: \times \: 21}{100} \)

S.I = $15,750

Amount = (P + S.I)

= 2,500 + 15,750

= $40,750

Amount paid each year

⇒ \( \frac{40750}{2} \)

Answer = $20,375.00

2021 WAEC Mathematics Essay Question 1b

Question

Two consecutive numbers are such that the sum of thrice the smaller and twice the larger is 17. Find correct to three significant figures, the smaller number as a percentage of the sum of the two numbers.

Solution

Let the consecutive numbers be x + 1 and x + 2

3(x + 1) + 2(x + 2) = 17

3x + 3 + 2x + 4 = 17

5x + 7 =17

5x = 17 – 7

5x = 10

x = \( \frac{10}{5} \)

x = 2

Since the consecutive numbers are x + 1 and x + 2

The numbers are;

2 + 1 = 3

2 + 2 = 4

smallest = 3

total number = 3 + 4 = 7

percentage = \( \frac{3}{7} \scriptsize \: \times \: 100 \% \)

= 42.857%

Answer = 42.9% (3 s.f)

2021 WAEC Mathematics Essay Question 2

Question

A man left town M at 10.00a.m. and travelled by car to town N at an average speed of 72km/h.  He spent 2 hours for a meeting and returned to town M by bus at an average speed of 40km/h. If the distance covered by the bus was 2km longer than that of the car and he arrived at town M at 1:55p.m., calculate the distance from M to N.

Solution

Start time = 10.00am

= 10 hrs

time spent travelling = 1.55pm

⇒ 12.00 + 1.55 = 13.55hrs

⇒ 13.55 hrs – 10hrs = 3.55 hrs

meeting time = 2hrs

Time on road = 3 hrs 55m – 2hrs = 1hrs 55min

1hr 55 mins = \( \frac{115}{60} \scriptsize \: hours  \\ = \frac{23}{12} \scriptsize \: hours\)

Let ‘x’ be distance from M to N and ‘t’ be time spent from M to N

Speed = \( \frac{distance}{time} \)

72 = \( \frac{x}{t} \)

t = \( \frac{x}{72} \)….(i)

Return time = \( \frac{23}{12} \scriptsize \: – \: t \)

⇒ \( \normalsize \frac{23}{12} \scriptsize \: -\: t = \normalsize \frac{x\:+\:2}{40}\)

⇒ \(  \frac{23}{12}\: -\: \frac{x}{72} =  \frac{x\:+\:2}{40}\)

⇒ \(  \frac{138\:-\:x}{72} =  \frac{x\:+\:2}{40}\)

40(138 – x) = 72(x + 2)

690 – 5x = 9x + 18

9x + 5x = 690 – 18

14x = 672

x = \( \frac{672}{14} \)

x = 48km

Answer ⇒  x = 48km

2021 WAEC Mathematics Essay Question 3

Question

The points X, Y and Z are located such that Y is 15km south of X, Z is 20km from X on a bearing of 270º. Calculate, correct to:

(a) two significant figures,  |YZ|

(b) the nearest degree, the bearing of Y from Z

 

(a) to two significant figures,  |YZ|

Solution

Using Pythagoras Theorem

⇒ \(\scriptsize |YZ|^2 = 15^2 \: + \: 20^2  \\ \scriptsize = 225 \: + \: 400 \\ \scriptsize = |YZ|^2 = 625 \\\scriptsize = |YZ| = \sqrt{625} \\ \scriptsize|YZ| = 25 \: km \)

Answer ⇒  |YZ| = 25km

 

(b) to the nearest degree, the bearing of Y from Z

Solution

tan θ = \(  \frac{15}{20} \)

θ = \( \scriptsize tan^{-1} \left( \frac{15}{20}\right) \)

θ = 26.8699º

Bearing of Y from Z

= 90° + 36.8699

= 126.8699

Answer   \( \scriptsize \simeq  127^o\)

2021 WAEC Mathematics Essay Question 4

Question

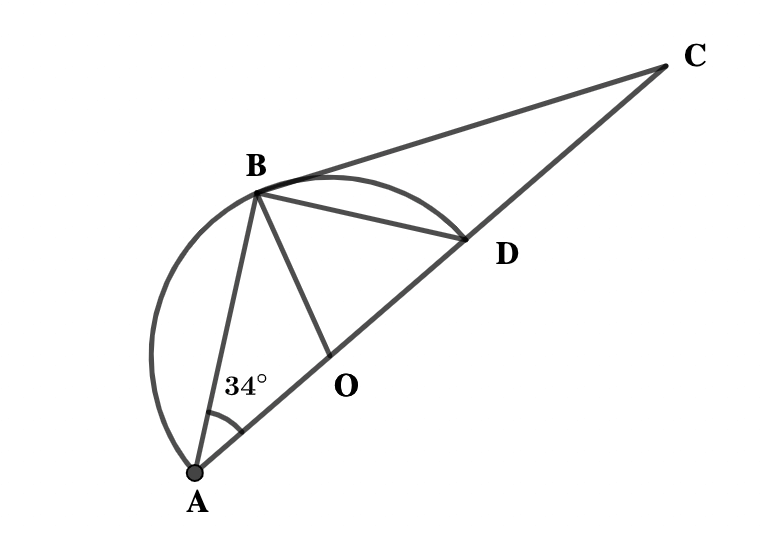
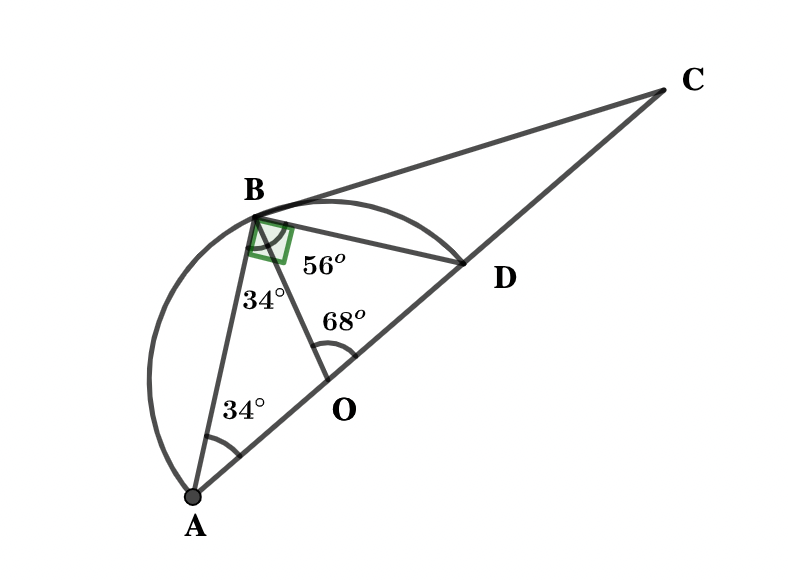
NOT DRAWN TO SCALE

In the diagram, \( \scriptsize \bar{AD} \) is a diameter of a circle with centre O. If ABD is a triangle in a semi-circle and ∠OAB = 34º,

find: (a) ∠OBD (b) ∠OCB

 

(a) ∠OBD

Solution

⇒ \(  \scriptsize \hat{OAB} = \hat{OBA} = 34^o \)

(base angles of an isosceles triangle)

⇒ \(  \scriptsize \hat{ABD} = 90^o \)

(angles in a semi-circle)

∴ \(  \scriptsize \hat{OBD} = \hat{ABD} \: – \: \hat{OBA} \)

= 90º – 34º

= 56°

Answer:  ∠OBD = 56°

 

(b) ∠OCB

Solution

⇒ \(  \scriptsize \hat{BOC} \: + \:  \hat{OBC} \: + \: \hat{OCB} = 180^o \)

(sum of angles in a triangle)

⇒ \(  \scriptsize \hat{BOD} = \hat{OAB} \: + \: \hat{OBA} \)

(sum of two opp. interior = exterior)

⇒ \(  \scriptsize \hat{BOD}  = 34 + 34 \)

⇒ \(  \scriptsize \hat{BOD}  = 68^o \)

Consider ΔOCB

⇒ \(  \scriptsize \hat{OBC}  = 90^o \)

(angles in a semi-circle)

∴ \( \scriptsize 68^o \: + \: 90^o \: + \: \hat{OCB} = 180^o \)

⇒ \(  \scriptsize \hat{OCB}  = 180^o \: -\: 158^o \)

⇒ \(  \scriptsize \hat{OCB}  = 22^o \)

Answer ⇒  \(  \scriptsize \hat{OCB}  = 22^o \)

2021 WAEC Mathematics Essay Question 5

Question

(a) A man shared his property among his children as follows:

Represent the information on a pie chart

Solution

Child’s Name  Percentage Angle (Deg)
Ann 5 \( \frac{5}{100} \scriptsize \: \times \: 360^o = 18^o\)
Afia 15 \( \frac{15}{100} \scriptsize \: \times \: 360^o = 54^o\)
Kojo 10 \( \frac{10}{100} \scriptsize \: \times \: 360^o = 36^o\)
Nuno 45 \( \frac{45}{100} \scriptsize \: \times \: 360^o = 162^o\)
Akosua 25 \( \frac{25}{100} \scriptsize \: \times \: 360^o = 90^o\)
Total 100 \( \scriptsize 360^o \)

Answer

 

(b) A box contains 5 red, 3 green and 4 blue identical beads. Calculate the probability that a girl takes away two red beads, one after the other, from the box.

Solution

5 Red, 3 Green, 4 Blue

Total beads = 5 + 3 + 4 = 12

Pro. (taking the 1st red) = \( \frac{5}{12} \)

Pro. (taking the 2nd red) = \( \frac{4}{11} \)

Pro. (two red beads) = \(\frac{5}{12} \: \times \: \frac{4}{11} \)

Answer = \(\frac{5}{33} \)

2021 WAEC Mathematics Essay Question 6a

Question

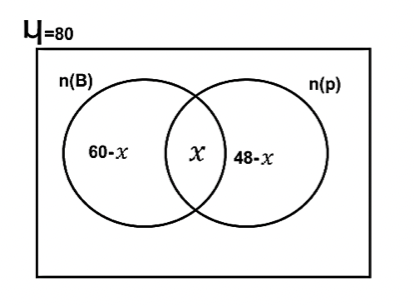
(a) In a class of 80 students, \( \frac{3}{4} \) study Biology and \( \frac{3}{5} \) study Physics. if each student studies at least one of the subjects.

(i) draw a venn diagram to represent this information

Solution

U = 80

n(B) = \(\frac{3}{4}\)

n(P) = \(\frac{3}{5}\)

Answer

Biology = \( \frac{3}{4} \scriptsize \: \times \: 80 = 60 \)

Physics = \( \frac{3}{5} \scriptsize \: \times \: 80 = 48 \)

 

(ii) how many students study both subjects;

Solution

80 = 60 – x + x  + 48 – x

80 = 108 – x

x  = 108 – 80

x = 28

Answer = 28

 

(iii) find the fraction of the class that study Biology but not Physics.

Solution

fraction = \( \frac{60 \:-\:28}{80}\)

= \( \frac{32}{80}\)

Answer = \( \frac{2}{5}\)

2021 WAEC Mathematics Essay Question 6b

Question

Johnson and Jocatol Ltd. Owned a business office with floor measuring 15m by 8m which was to be carpeted. The cost of carpeting was GHȼ890.00 per square metre. If a total of GHȼ216,120.00 was spent on painting and carpeting, how much was the cost of painting?

 

Solution

Area of floor = 15 x 18

= 120m2

cost of carpeting = 120 x 98 = 106800

cost of painting = 216,120 – 106,800

Answer = GHȼ 109,320.00

2021 WAEC Mathematics Essay Question 7

Question

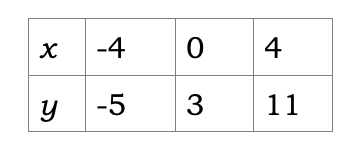
(a) Copy and complete the table of values for the relation:

⇒ \( \scriptsize y = 2x^2 \: -\: x \: -\: 2 \\ \scriptsize\: for \: -4 \leq x \leq 4 \)

 

Solution

 

 

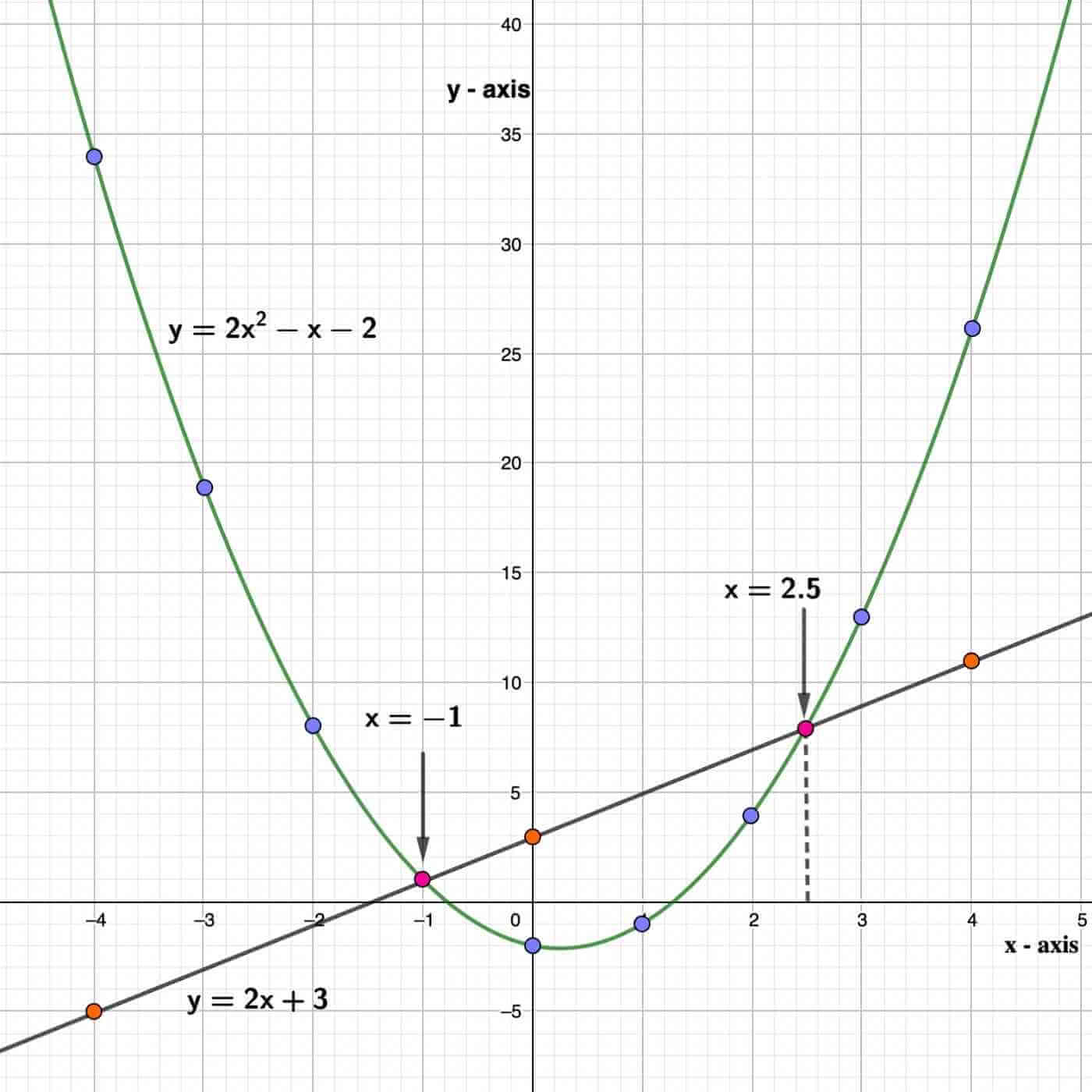
(b) Using a scale of 2cm to 1 unit on the x-axis, and 2cm to 5 units on the y – axis, draw the graph of

⇒ \( \scriptsize y = 2x^2 \: -\: x \: -\: 2 \\ \scriptsize\: for \: -4 \leq x \leq 4 \)

 

Solution

 

(c) On the same axes, draw the graph of   y = 2x + 3

Solution

 

(d) Use the graph to find the:

(i) roots of the equation \( \scriptsize 2x^2 \: – \: 3x \: – \: 5 = 0 \)

Solution

Answer⇒ x = -1 and x = 2.5

(ii) range of values for which \( \scriptsize 2x^2 \: – \: x \: – \: 2 < 0 \)

range of values of x

Answer⇒  \( \scriptsize -0.8 < x < 1.2 \)

2021 WAEC Mathematics Essay Question 8a

Question

In ΔPQR, ∠PQR = 90º. If its area is 216cm² and |PQ|:|QR| is 3:4

Find |PR|

Solution

A = \( \frac{1}{2} \scriptsize  |PQ||QR| sin \theta \)

216 = \( \frac{1}{2} \scriptsize  |PQ||QR| sin 90 \)

⇒ \( \frac{|PQ|}{|QR|} = \frac{3}{4}\)

⇒ \( \scriptsize |PQ| = \normalsize \frac{3}{4} \scriptsize |QR| \)

216 = \( \frac{1}{2} \: \times \: \frac{3}{4} \scriptsize |QR| |QR| \: \times \: 1 \)

216 = \( \frac{3}{8}  \scriptsize |QR|^2  \)

⇒ \( \scriptsize |QR|^2 = \normalsize \frac{216 \: \times \: 8}{3} \)

⇒ \( \scriptsize |QR| = \sqrt{576} \)

⇒ \( \scriptsize |QR| = 24 \: cm\)

⇒ \( \scriptsize |PQ| = \normalsize \frac{3}{4} \: \scriptsize |QR| \)

⇒ \( \scriptsize |PQ| = \normalsize \frac{3}{4} \scriptsize \: \times \: 24 = 18cm \)

⇒ \( \scriptsize |PR|^2 =  18^2 \: + \: 24^2 \)

⇒ \( \scriptsize |PR| = \sqrt{18^2 \: + \: 24^2}\)

⇒ \( \scriptsize |PR| = \sqrt{900}\)

⇒ \( \scriptsize |PR| = 30 \: cm\)

Answer⇒  \( \scriptsize |PR| = 30 \: cm\)

2021 WAEC Mathematics Essay Question 8b

Question

The present ages of a man and his son are 47 years and 17 years respectively. In how many years would the man’s age be twice that of his son?

Solution

let x be the number of years

Man’s age = 47

Son’s age = 17

∴ 47 + x = 2(17 + x)

47 + x = 34 + 2x

2x – x = 47 – 34

x = 13 yrs

Answer⇒  x = 13 yrs

2021 WAEC Mathematics Essay Question 9

Question

NOT DRAWN TO SCALE

In the diagram, PQRS is a trapezium with \( \scriptsize \bar{QR} || \bar{PS} \)

U and T are points on \( \scriptsize \bar{PS} \) such that \( \scriptsize \bar{PU}  = 5cm, \:\bar{QU} = 12cm\)

and ∠PUQ = ∠STR =90°. If the area of ΔUQR = 20 cm2, calculate to the nearest whole number, the:

(a) Perimeter of the trapezium.

Solution

Area of ΔUQR = \( \frac{1}{2} \scriptsize \: \times \: b \: \times \: h \)

20 = \( \frac{1}{2} \scriptsize \: \times \: b \: \times \: 12 \)

40 = 12b

b = \( \frac{40}{12} \scriptsize = 3.33\:cm \)

b = |QR| = |UT| = 3.33cm

⇒ \( \scriptsize |PQ|^2 = 12^2 \: + \: 5^2 \)

⇒ \( \scriptsize |PQ|^2 = 144 \: + \: 25 \)

⇒ \( \scriptsize |PQ|^2 = 169 \)

⇒ \( \scriptsize |PQ| = \sqrt{169} \)

⇒ \( \scriptsize |PQ| = 13\:cm \)

⇒ \( \scriptsize |QU| = |RT| = 12\:cm \)

ΔRTS

sin 50º = \( \frac{12}{RS} \)

|RS| = \( \frac{12}{sin\:50^o} \)

|RS| = 15.6649cm

tan 50º = \( \frac{12}{TS} \)

|TS| = \( \frac{12}{tan\:50^o} \)

|TS| = 10.069cm

Perimeter = addition of all boundaries

p = |PQ| + |QR| + |RS| + |TS| + |UT| + |PU

P = 13 + 3.33 + 15.6649 + 10.069 + 3.33 + 5

p = 50.3939

p ≅ 50 cm ( nearest whole number)

Answer⇒  Perimeter ≅ 50 cm

 

(b) Area of the trapezium.

Solution

Area of trapezium = \( \frac{1}{2} \scriptsize h(a \: + \: b)\)

A = \( \frac{1}{2} \scriptsize \: \times \:  12(QR \: + \: PS)\)

|PS| = 5 + 3.33 + 10.069 = 18.399

A = \( \frac{1}{2} \scriptsize \: \times \:  12(3.33 \: + \: 18.399)\)

A = 6(21.729)

= 130.374cm2

A ≅ 130cm2 (nearest whole number)

Answer⇒  Area ≅ 130cm2

2021 WAEC Mathematics Essay Question 10

Question

(a) A cottage is on a bearing of 200° and 110° from Dogbe’s and Manu’s farms respectively. If Dogbe walked 5km and Manu 3km from the cottage to their farms, find:

(i) correct to two significant figures, the distance between the two farms;

 

Solution

Distance (?) = \( \scriptsize \sqrt{3^2 + 5^2} \)

= \( \scriptsize \sqrt{9 + 25} \)

= \( \scriptsize \sqrt{34} \)

= \( \scriptsize 5.831km\)

≅ \( \scriptsize 5.8km\)

Answer⇒  Distance between two farms ≅ 5.8km

 

(ii) correct to the nearest degree, the bearing of Manu’s farm from Dogbe’s.

tan θ = \( \frac{3}{5} \)

tan θ = 0.6

θ = \( \scriptsize tan^{-1} 0.6 \)

θ = 30.9638º

Bearing = 30.9638 + 200

= 230.9638

Answer⇒  the bearing of Manu’s farm from Dogbe’s ≅ 231º (nearest degree)

 

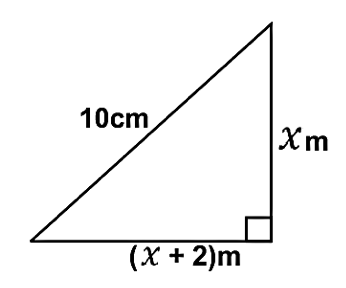
(b) A ladder 10m long leaned against a vertical wall  high. The distance between the wall and the foot of the ladder is 2m longer than the height of the wall. Calculate the value of  x

Solution

⇒ \( \scriptsize 10^2 = (x \: + \: 2)^2 \: + \: x^2 \)

⇒ \( \scriptsize 100 = (x \: + \: 2)(x \:+\:2) \: + \: x^2 \)

⇒ \( \scriptsize 100 = x^2 \: + \: 2x \: + \: 2x \: + \: 4\: + \: x^2 \)

⇒ \( \scriptsize 100 = 2x^2 \: + \: 4x \: + \: 4 \)

⇒ \( \scriptsize 2x^2 \: + \: 4x \: + \: 4  \: -\: 100 = 0\)

⇒ \( \scriptsize 2x^2 \: + \: 4x \: –  \: 96= 0\)

divide through by 2

⇒ \( \scriptsize x^2 \: + \: 2x \: –  \: 48 = 0\)

factorise

⇒ \( \scriptsize x^2 \: + \: 8x \: – \: 6x \: –  \: 48 = 0\)

⇒ \( \scriptsize x(x \: + \: 8) \: – \: 6(x \: + \: 8) = 0\)

⇒ \( \scriptsize (x \: – \: 6)(x \: + \: 8) \)

x – 6 = 0 or x + 8 = 0

x = 6 or -8

Length can’t be negative

∴ x = 6m

Answer⇒  x = 6m

2021 WAEC Mathematics Essay Question 11

Question

The table shows the distribution of the number of hours per day spent in studying by 50 students

Calculate, correct to two decimal places, the:

(a) Mean;

Solution

X F fx Fx2
4 5 20 80
5 7 35 175
6 5 30 180
7 9 63 441
8 12 96 768
9 4 36 324
10 3 30 300
11 5 55 605
  ΣF=50 ΣFx=365 ΣFx2=2873

⇒ \(\scriptsize mean \: \bar{X} = \normalsize  \frac{\sum Fx}{\sum F} \)

=\( \frac{365}{50} \)

⇒ \(\scriptsize mean \: \bar{X} = 7.30\: (2d.p) \)

Answer ⇒  mean – 7.30 (2d.p)  

 

(b) Standard deviation

Solution

S.D = \( \sqrt{\frac{\sum Fx^2}{\sum F} \: -\: \left( \frac{\sum Fx}{\sum F}\right)^2} \)

S.D = \( \sqrt{\frac{2873}{50} \: -\: \left( \scriptsize 7.3 \right )^2} \)

= \( \scriptsize \sqrt{57.46 \: -\: 53.29} \)

= \( \scriptsize \sqrt{4.17} \)

= 2.0421

≅ 2.04 (2 d.p)

Answer ⇒  ≅ 2.04 (2 d.p)

2021 WAEC Mathematics Essay Question 12

Question

(a)

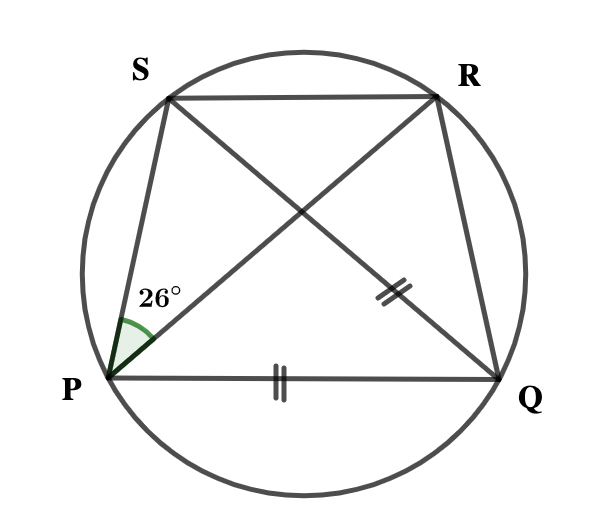
In the diagram, PQRS is a circle. |PQ| = |QS|, ∠SPR = 26º and the interior of angles of ΔPQS are in the ratio 2:3:3.

Calculate:

(i) ∠PQR
(ii) ∠RPQ
(iii) ∠PRQ

 

Solution

(a. i) ∠PQR

∠PSQ = ∠QPS

(base angles of isosceles)

Total ratio = 2 + 3 + 3

= 8

⇒ \( \scriptsize \angle PQS = \normalsize \frac{2}{8} \scriptsize  \: \times \: 180^o \\ \scriptsize = 45^o \)

⇒ \( \scriptsize \angle SPQ = \angle PSQ = \normalsize \frac{3}{8}\scriptsize \: \times \: 180^o \\ \scriptsize = 67.5^o \)

⇒ \( \scriptsize \angle SQR = \angle SPQ = 26^o \)

⇒ \( \scriptsize \angle PQR = \angle PQS\: +\:\angle SRQ \)

= 45º + 26º

Answer ⇒  = 71º

 

(a.ii ) ∠RPQ

∠RPQ = ∠SPQ – ∠SPR

= 67.5º – 26º

Answer ⇒  = 41.5º

 

(a.iii) ∠PRQ

∠PRQ = 180 – 41.5 – 71

Answer ⇒ = 67.5º

 

(b) The coordinates of two points P and Q in a plane are (7, 3) and (5, x) respectively, where x is a real number.

If \( \scriptsize |PQ| = \sqrt{29} \: units, \) find the value of x

Solution

⇒ \( \scriptsize PQ^2 = (x_2 \: -\: x_1)^2 \: + \: (y_2 \: -\: y_1)^2 \)

⇒ \( \scriptsize PQ = (x_2 \: -\: x_1)^2 \: + \: (y_2 \: -\: y_1)^2 \)

⇒ \( \scriptsize x_2 = 5, \: x_1 = 7 \)

⇒ \( \scriptsize y_2 = x, \: y_1 = 3 \)

⇒ \( \scriptsize \sqrt{29} = \sqrt{(5\:-\:7)^2 \: +\: (x \: -\: 3)^2} \)

⇒ \( \scriptsize 29 = (-2)^2 \: + \: (x \: – \: 3)(x\:-\:3) \)

⇒ \( \scriptsize 29 = 4 \: + \: x^2 \: -\: 3x \: -\: 3x \: +\: 9 \)

⇒ \( \scriptsize 29 = 4 \: + \: x^2 \: -\: 6x \: +\: 9 \)

⇒ \( \scriptsize   x^2 \: -\: 6x \: +\: 9\: + \: 4 \: -\: 29 = 0 \)

⇒ \( \scriptsize   x^2 \: -\: 6x \: – \: 16= 0 \)

⇒ \( \scriptsize   x^2 \: -\: 8x \: + \: 2x \: – \: 16= 0 \)

⇒ \( \scriptsize   x(x \: -\: 8) \: +\: 2(x \: -\: 8) = 0 \)

⇒ \( \scriptsize   (x \: + \: 2)(x\:-\:8) = 0\)

x + 2 = 0 or x – 8 = 0

Answer ⇒  x = -2 or x = 8

2021 WAEC Mathematics Essay Question 13

Question

(a) On Sam’s first birthday celebration, his grandfather deposited an amount of $1,000.00 in a bank compounded at 4% interest annually. Find how much is in the account if Sam is 4 years old.

Solution

Amount at end of 2nd year

= \( \frac{104}{100}\scriptsize \: \times \: 1000 \)

= $1040

Amount at end of 3rd year

= \( \frac{104}{100}\scriptsize \: \times \: 1040 \)

= $1081

Amount at end of 4th year

= \( \frac{104}{100}\scriptsize \: \times \: 1081 \)

Answer ⇒ = $1124.86

 

(b)

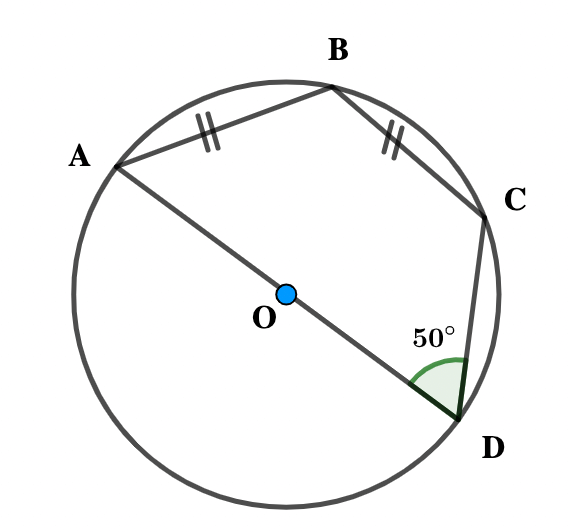
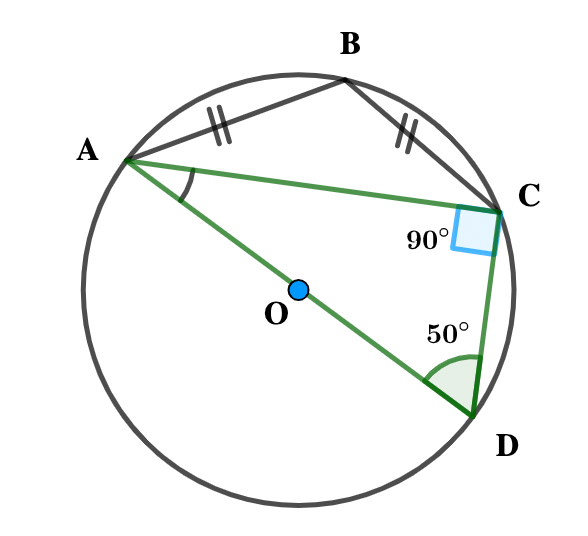
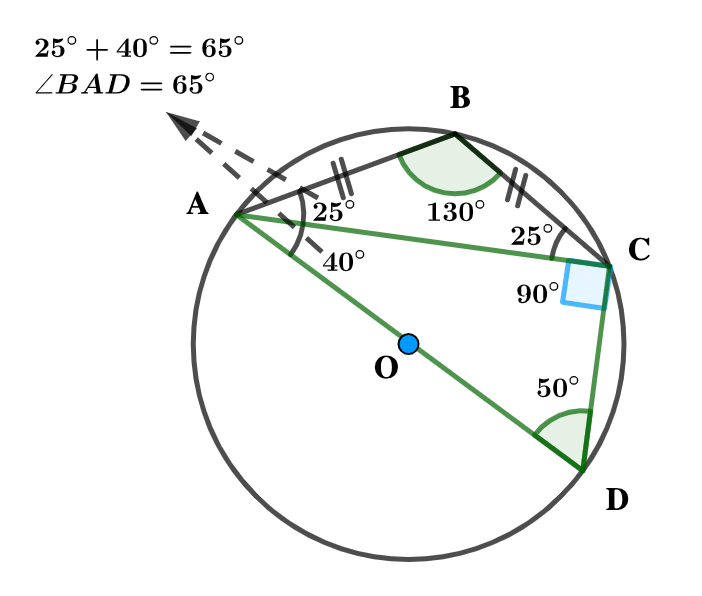
NOT DRAW TO SCALE

In the diagram, ABCD are points on the circle O.

If |AB| = |BC| and ∠ADC = 50º, find ∠BAD

Solution

⇒ \( \scriptsize \angle DCA =90^0 \)

(angles in a semi-circle)

⇒ \( \scriptsize \angle DCA \: + \: \angle ADC \: + \: \angle CAD =180^0 \)

(angles in a triangle)

⇒ \( \scriptsize 90^o\: + \: 50^o \: + \: \angle CAD =180^0 \)

⇒ \( \scriptsize \angle CAD =180^0 \: -\: 140^o \)

= 40º

⇒ \( \scriptsize \angle ADC \: + \: \angle ABC  = 180^0 \)

(cyclic quadrilateral)

⇒ \( \scriptsize 50 \: + \: \angle ABC  = 180^0 \)

⇒ \( \scriptsize \angle ABC  = 180^0 \: – \: 50^o \)

⇒ \( \scriptsize \angle ABC  = 130^o \)

⇒ \( \scriptsize \angle BAC =  \angle BCA \)

(base angles of isosceles)

⇒ \( \scriptsize \angle BAC \: + \: \angle BCA \: + \: \angle ABC = 180^o \)

(sum of angles in a triangle)

⇒ \( \scriptsize 2 \angle BAC \: + \: 130^o = 180^o \)

⇒ \( \scriptsize 2 \angle BAC  = 180^o \: – \: 130^o \)

⇒ \( \scriptsize 2 \angle BAC  = 50^o \)

⇒ \( \scriptsize \angle BAC  = \normalsize \frac{50}{2} \)

⇒ \( \scriptsize \angle BAC  = 25^o \)

⇒ \( \scriptsize \angle BAD  = \angle BAC \: + \: \angle CAD\)

⇒ \( \scriptsize \angle BAD  = 25 \: + \: 40\)

⇒ \( \scriptsize \angle BAD  = 65^o\)

Answer ⇒ \( \scriptsize \angle BAD  = 65^o\)

Report

Harassment or bullying behavior
Contains mature or sensitive content
Contains misleading or false information
Contains abusive or derogatory content
Contains spam, fake content or potential malware

Block Member?

Please confirm you want to block this member.

You will no longer be able to:

  • See blocked member's posts
  • Mention this member in posts
  • Invite this member to groups
  • Message this member
  • Add this member as a connection

Please note: This action will also remove this member from your connections and send a report to the site admin. Please allow a few minutes for this process to complete.

Report

You have already reported this .
error: Alert: Content selection is disabled!!