Topic Content:
- Perimeter of a Rectangle
The longer side of a rectangle is usually called the length, and the shorter side is the breadth.
length = l
breadth = b
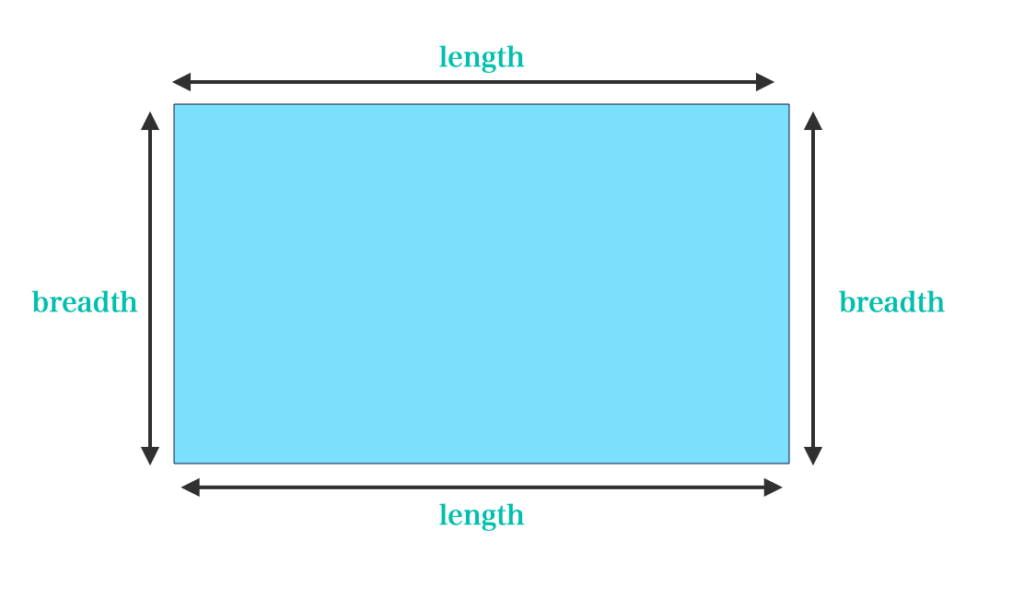
Perimeter of rectangle = \( \scriptsize l \: + \: b \: + \: l \: + \: b \\ = \scriptsize l \: + \: l \: + \: b \: + \: b \\ = \scriptsize 2l \: + \: 2b \\ = \scriptsize 2(l \: + \: b) \)
Perimeter of a Rectangle = 2l + 2b
Where l = Length
b = breadth
breadth (b) is also known as width (w)
Example 7.3.1:
The length of a rectangular room is 8 m, and the width (breadth) is 6 m. Find the perimeter of the room.
Solution:
Length of the room, l = 8 m
You are viewing an excerpt of this Topic. Subscribe Now to get Full Access to ALL this Subject's Topics and Quizzes for this Term!
Click on the button "Subscribe Now" below for Full Access!
Subscribe Now
Note: If you have Already Subscribed and you are seeing this message, it means you are logged out. Please Log In using the Login Button Below to Carry on Studying!



Responses