Multiplier & Shunt

Multiplier

A small galvanometer which is used for measuring small current can be converted to a multiplier. This is achieved by connecting a high resistance (resistor) in series with the galvanometer in order to convert it to voltmeter

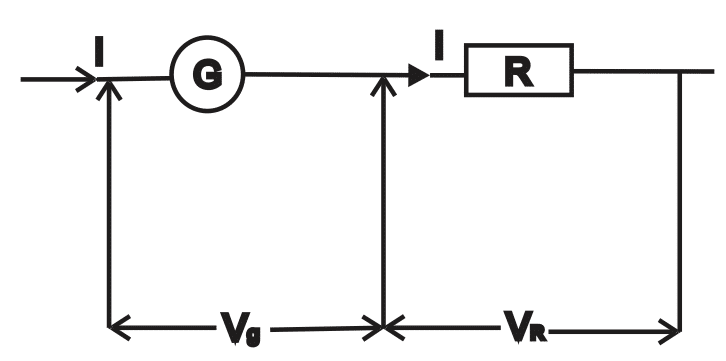
V = V_g+ V_R

V = Voltage across the whole circuit

V_g = voltage along the galvanometer

V_m = voltage across the multiplier

R_g = resistance across the galvanometer

R_m = resistance across the multiplier

Since galvanometer and multiplier are in the same series, the same amount of current flows through them

I = \( \frac {V_g}{R_g} = \frac {V_m}{R_m} = \frac {V_r}{R_m} \)

Example

A galvanometer of resistance 6Ω and full scale deflection (f.s.d) of 50MA is used to measure a P.d of 60V. Calculate the resistance of the multiplier.

Solution 

Galvanometer current = 50MA = 0.05A

Voltage across galvanometer V_g = IR_g = 0.05 × 6 = 0.30V

Voltage across multipliers, V = V_g + R_m

    60 = 0.30 + V_m 

V_m  = 60 – 0.30 = 59.7V

The galvanometer and multiplier are in series, the same current passes through them;

\( \frac {V_g}{R_g} = \frac {V_m}{R_m}\)

\( \frac {0.3}{6} = \frac {59.7}{R_m}\)

 R_m =\( \frac {59.7 \times 6}{0.30}\)

R_m = \( \frac {35.82}{0.30}\)

 R_m = 1191Ω

Shunt

A low resistance (resistor) connected in parallel across a galvanometer to convert it to ammeter is called shunt.

R_g = resistance of the galvanometer

I_g = current in the galvanometer

R_s = resistance of the shunt

I_s = current in the shunt

From the diagram

I = I_g + I_s

Since the same P.d passes through them, being parallel,

V_g =  V_s

I_gR_g = I_sR_s

Example:

A galvanometer of resistance 3Ω has an f.s.d for a current of 100MA. Calculate the resistance of the shunt required to convert it to a 5A ammeter

Solution

I_g = 100MA, R_g =3Ω

I = I_g + I_s

5 = 0.1 + I_s

5 – 0.1 = I_s 

I_s = 4.9A

V_g =  V_s 

I_g x R_g = I_s x R_s

R_s  = \( \frac{0.1 \times 3 }{49} \)

=0.06Ω