Antilog Table

The Antilog, or “Anti- Logarithm” of a number is the inverse technique of finding the logarithm of the same number. i.e., if log x = y then x = antilog (y)

log x = y ⇒ x = antilog (y)

For example:

• log 1000 = 3, antilog (3) = 10³ = 1000
• log 100 = 2, antilog (2) = 10² = 100

When finding an antilogarithm, we use the anti-log table, look up the mantissa and then use the characteristic to fix the decimal point correctly to the answer.

Below is the antilog table for the common logarithm.

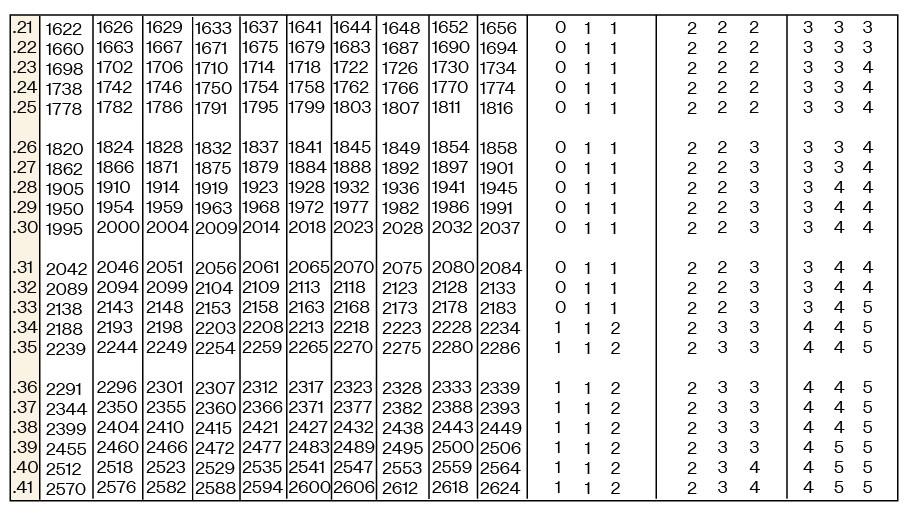
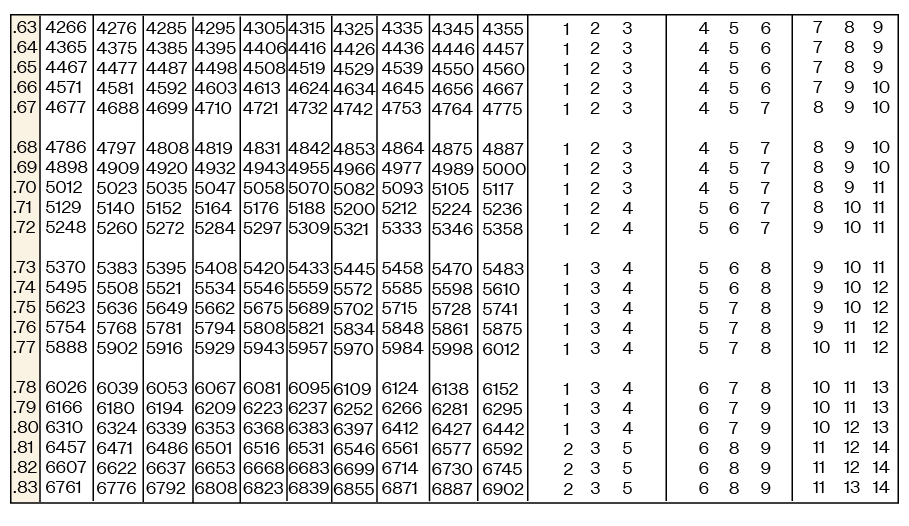
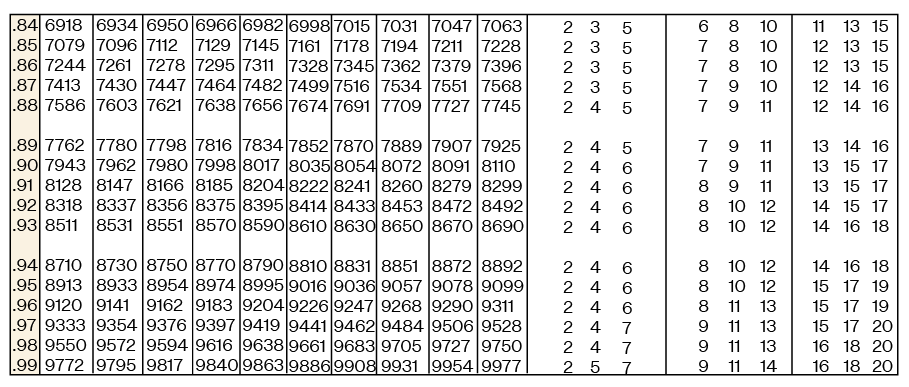
Example 10.2.1 – How to Use the Antilog Table:

Each of the following indicial systems is in the form y = 10^x, use the antilogarithm table to find the decimal number y.

(a) 10^0.2318
(b) 10^1.2574
(c) 10^2.2296

Solution

(a) Let y = 10^0.2318